陕西省西安市碑林区2021-2022学年八年级下学期开学数学试卷

试卷更新日期：2022-03-22 类型：开学考试

进入出卷网下载

一、选择题（每题3分，共计30分）

1. 下列各组数不是勾股数的是（）

A、3，4，5 B、5，12，13 C、7，24，25 D、0.6，0.8，1

查看试题解析
2. 在给出的一组数0，π， $\sqrt{5}$ ，3.14， $\frac{22}{7}$ 中，无理数有（）

A、1个 B、2个 C、3个 D、5个

查看试题解析
3. 下列实数运算中正确的是（）

A、 $\sqrt{{(- 7)}^{2}}$ ＝﹣7 B、 $\sqrt{48}$ ＝4 $\sqrt{3}$ C、（﹣ $\sqrt{2}$ ）²＝4 D、 $\sqrt{9}$ ＝±3

查看试题解析
4. 下列命题是假命题的是（）

A、同位角相等 B、三角形内角和是180° C、内错角相等，两直线平行 D、三角形的一个外角大于任何一个和它不相邻的内角

查看试题解析
5. 若点A（m，n）在第二象限，则点A′（m，﹣n）在第（）象限．

A、一 B、二 C、三 D、四

查看试题解析
6. 一次函数y＝﹣2x+6的图象与y轴的交点坐标是（）

A、（0，6） B、（6，0） C、（3，0） D、（0，3）

查看试题解析
7. 一次函数y＝kx﹣k的大致图象可能如图（）

A、 B、 C、 D、

查看试题解析
8. 将直线y＝﹣3x沿着x轴向右平移2个单位，所得直线的解析式为（）

A、y＝﹣3x+2 B、y＝﹣3x﹣2 C、y＝﹣3x﹣6 D、y＝﹣3x+6

查看试题解析
9. 若关于x，y的方程组 ${\begin{array}{l} x + 2 y = 2 k \\ 4 x - y = 5 k \end{array}$ 的解x，y满足x-y=1，则k的值为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 已知直线y＝k₁x+b₁与直线y＝k₂x+b₂的交点坐标为（3，﹣5），则直线y＝k₁x﹣b₁与直线y＝k₂x﹣b₂的交点坐标为（）

A、（3，5） B、（﹣3，5） C、（﹣3，﹣5） D、（3，﹣5）

查看试题解析

二、填空题（每题3分，共计18分）

11. 有理数16的算数平方根是．

查看试题解析
12. 已知点A（1，4），B（0，2），C（4，0），则△ABC的周长为．

查看试题解析
13. 已知数据x₁ ， x₂ ， ....，x_n的方差为3，则数据2x₁﹣7，2x₂﹣7，…，2x_n﹣7的方差为．

查看试题解析
14. 直线y＝2x﹣3关于y轴对称后得到直线．

查看试题解析
15. 在平面直角坐标系中，点P（﹣4，﹣2）关于直线y＝﹣x对称的点P′的坐标为．

查看试题解析
16. 如图，已知Rt△ABC，∠C=90°，AC=BC=2，点M，N分别为CB，CA上的动点，且始终保持BM=CN，则AM+BN的最小值为．

查看试题解析

三、解答题（共计72分）

17. 计算：

(1)、（1﹣ $\sqrt{3}$ ）×（2+ $\sqrt{12}$ ）；

(2)、 $\sqrt{13^{2} - 12^{2}} - \sqrt[3]{- 27}$ +（3﹣ $\sqrt{3}$ ）（3+ $\sqrt{3}$ ）．

查看试题解析
18. 解方程组：

(1)、 ${\begin{array}{l} x - 2 y = - 2 \\ 2 x - y = 2 \end{array}$

(2)、 ${\begin{array}{l} 4 (x - y - 1) = 3 (1 - y) - 2 \\ \frac{x}{2} + \frac{y}{3} = 2 \end{array}$

查看试题解析
19. 尺规作图题：如图.四边形ABCD，AD∥BC，请在边AD上找一点M，使得MC平分∠BMD.请作出点M.（要求：尺规作图不写作法，保留作图痕迹），

查看试题解析
20. 某校为了解学生的手算能力，随机抽取八年级的部分学生就数学中的计算题做了测试.测试的结果分为四个等级：优秀、良好、合格、不合格；根据调查结果绘制了下列两幅不完整的统计图，请你根据以上统计图提供的信息解答以下问题：

(1)、该手算检测结果的众数为；

(2)、补全上面的条形统计图；

(3)、若该校八年级有1600名学生，估计该校八年级手算能力为“不合格”的学生约有多少人？

查看试题解析
21. 如图，有一直角三角形纸片，两直角边AB=6cm，AC=8cm，现将直角边AB沿直线BD进行对折，使点A刚好落在斜边BC上，且与A'B重合，求BD的长，

查看试题解析
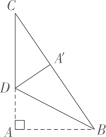22. 如图，平面直角坐标系中，点A（0，3）和B（4，0），点M（8，m）为坐标平面内一动点，且△ABM为等腰三角形，求点M的坐标，

查看试题解析
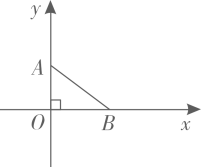23. 某商店分两次购进A、B两种商品进行销售，两次购进同一种商品的进价相同，具体情况如表：

A

B

购进费用/元

第一次购进数量/件

20

30

2800

第二次购进数量/件

30

20

2200

(1)、求A、B两种商品每件的进价分别是多少元？（要求用二元一次方程组求解）

(2)、商场决定将A种商品以每件30元出售，将B种商品以每件100元出售，为了满足市场需求，需购进A、B两种商品共1000件，且A种商品的数量等于B种商品数量的4倍，请求出所有商品卖出后的总利润。

查看试题解析
24. 问题探究

(1)、已知直线y＝kx+b经过点A（﹣3，0），B（0，﹣ $\sqrt{3}$ ），当 $- \sqrt{3} \leq x \leq 2 \sqrt{3}$ 时，求y的最小值．

(2)、如图1，等边△ABC中，AB=2，点D为边BC的中点，连接AD，求∠CAD及CD：AC：AD的值；

(3)、问题解决：如图2，在平面直角坐标系中，直线l与x轴、y轴分别交于点M、E，已知点M（-3，0），且∠EMO＝60°，点A（4， $\sqrt{3}$ ），B（2，﹣ $\sqrt{3}$ ），C（﹣1，﹣2 $\sqrt{3}$ ），连接AB，BC，得到折线段A﹣B﹣C，点P为折线段A﹣B﹣C上一动点，过点P向直线l作垂线，垂足为H，过点P作x轴的平行线交直线于点Q，则△PHQ的周长是否存在最大值或最小值？若存在，求出相应最值；若不存在，请说明理由.

查看试题解析

	A	B	购进费用/元
第一次购进数量/件	20	30	2800
第二次购进数量/件	30	20	2200