广西桂林、崇左、贺州市2022届高三理数3月高考联合调研考试试卷

试卷更新日期：2022-03-22 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {- 1 ， 0 ， 1 ， 2}$ ， $B = {x | x^{2} < 4}$ ，则 $A ∩ B =$ （）

A、 ${- 1 ， 0 ， 1}$ B、 ${0 ， 1 ， 2}$ C、 ${1 ， 2}$ D、 ${- 1 ， 1 ， 2}$

查看试题解析
2. 在复平面内，复数 $\frac{1}{1 - i}$ 的共轭复数对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知等差数列 ${a_{n}}$ 的公差为1， $S_{n}$ 为其前 $n$ 项和，若 $S_{3} = a_{6}$ ，则 $a_{2} =$ （）

A、-1 B、1 C、-2 D、2

查看试题解析
4. 设函数 $f (x)$ 在 $R$ 上存在导函数 $f' (x)$ ， $f (x)$ 的图象在点 $M (1 ， f (1))$ 处的切线方程为 $y = \frac{1}{2} x + 2$ ，那么 $f (1) + f' (1) =$ （）

A、1 B、2 C、3 D、4

查看试题解析
5. 随机变量 $X$ 的分布列为
$X$
$- 1$
0
1
$P$
$a$
$\frac{1}{3}$
$c$
则 $P (| X | = 1)$ 等于（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{6}$

查看试题解析
6. 在 $△ A B C$ 中，内角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ ，若 $b = a s i n C ， c = a c o s B$ ，则 $△ A B C$ 的形状一定为（）

A、等腰三角形非直角三角形 B、直角三角形非等腰三角形 C、等腰直角三角形 D、等边三角形

查看试题解析
7. 长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的体积是120，若E为 $C C_{1}$ 的中点，则三棱锥 $E - B C D$ 的体积为（）

A、10 B、20 C、30 D、40

查看试题解析
8. 已知 $\sin (\frac{2 π}{3} + x) = \frac{3}{5}$ ，则 $\cos (x + \frac{7 π}{6})$ 等于（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $- \frac{3}{5}$ D、 $- \frac{4}{5}$

查看试题解析
9. 已知圆 $C$ 过点 $A (0 ， 2)$ 且与直线 $y = - 2$ 相切，则圆心 $C$ 的轨迹方程为（）

A、 $x^{2} = 4 y$ B、 $x^{2} = 8 y$ C、 $x^{2} = - 4 y$ D、 $x^{2} = - 8 y$

查看试题解析
10. 已知 $F$ 为双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左焦点，若双曲线右支上存在一点 $P$ ，使直线 $P F$ 与圆 $x^{2} + y^{2} = a^{2}$ 相切，则双曲线离心率的取值范围是（）

A、 $(\sqrt{2} ， + \infty)$ B、 $(\frac{\sqrt{2}}{2} ， + \infty)$ C、 $(0 ， \frac{\sqrt{2}}{2})$ D、 $(1 ， \sqrt{2})$

查看试题解析
11. 四面体 $P A B C$ 的四个顶点都在球 $O$ 的球面上， $P A = 8 ， B C = 4 ， P B = P C = A B = A C$ ，且平面 $P B C ⊥$ 平面 $A B C$ ，则球 $O$ 的表面积为

A、64π B、65π C、66π D、128π

查看试题解析
12. 函数 $f (x)$ 的导函数为 $f^{'} (x)$ ，对 $\forall x \in R$ ，都有 $2 f^{'} (x) > f (x)$ 成立，若 $f (l n 4) = 2$ ，则不等式 $f (x) > e^{\frac{x}{2}}$ 的解集是（）

A、 $(0 ， 1)$ B、 $(l n 4 ， + \infty)$ C、 $(1 ， + \infty)$ D、 $(0 ， l n 4)$

查看试题解析

二、填空题

13. 若函数 $f (x)$ 满足 $f (1 - l n x) = \frac{1}{x}$ ，则 $f (2)$ 等于.

查看试题解析
14. 已知向量 $\vec{a} ， \vec{b}$ ，满足 $| \vec{a} | = 1 ， | \vec{b} | = \sqrt{2}$ ，若 $\vec{a} ⊥ (\vec{a} + \vec{b})$ ，则向量 $\vec{a}$ 与向量 $\vec{b}$ 的夹角为．

查看试题解析
15. $(1 + x^{2}) {(1 - \frac{1}{x})}^{6}$ 的展开式中，常数项为.

查看试题解析
16. 为积板应对新冠肺炎疫情，提高大家对新冠肺炎的认识，某企业举办了“抗击疫情，共克时艰”预防新冠肺炎知识竞赛，知识竞赛规则如下：在预设的6个问题中，选手若能连续正确回答出3个问题，即停止答题，晋级下一轮.假定某选手正确回答每个问题的概率都是 $\frac{2}{3}$ ，且每个问题的回答结果相互独立，则该选手至少回答了5个问题晋级下一轮的概率等于.

查看试题解析

三、解答题

17. 记 $S_{n}$ 为等差数列 ${a_{n}}$ 的前 $n$ 项和，已知公差 $d \neq 0$ ， $S_{7} = 35$ ，且 $a_{2}$ ， $a_{5}$ ， $a_{11}$ 成等比数列.

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、若 $T_{n}$ 为数列 ${\frac{1}{a_{n} a_{n + 1}}}$ 的前 $n$ 项和，求 $T_{n}$ .

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中，底面 $A B C D$ 是平行四边形， $∠ B C D = 135 °$ ，侧面 $P A B ⊥$ 底面 $A B C D$ ， $∠ B A P = 90 °$ ， $A B = A C = P A = 2$ ， $E$ ， $F$ 分别为 $B C$ ， $A D$ 的中点，点 $M$ 在线段 $P D$ 上．

(1)、求证： $E F ⊥$ 平面 $P A C$ ；

(2)、如果直线 $M E$ 与平面 $P B C$ 所成的角和直线 $M E$ 与平面 $A B C D$ 所成的角相等，求 $\frac{P M}{P D}$ 的值．

查看试题解析
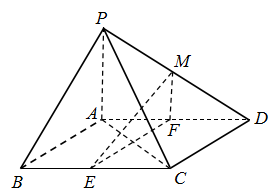19. （理）某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制，已知所有这些学生的原始成绩均分布在 $[50 ， 100]$ 内，发布成绩使用等级制各等级划分标准见下表，规定： $A 、 B 、 C$ 三级为合格等级， $D$ 为不合格等级.
百分制
85分及以上
70分到84分
60分到69分
60分以下
等级
$A$
$B$
$C$
$D$
为了解该校高一年级学生身体素质情况，从中抽取了 $n$ 名学生的原始成绩作为样本进行统计，按照 $[50 ， 60) ， [60 ， 70) ， [70 ， 80) [80 ， 90) ， [90 ， 100)$ 的分组作出频率分布直方图如图所示，样本中分数在80分及以上的所有数据的茎叶图如图所示.，

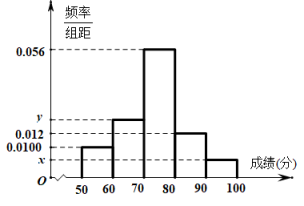
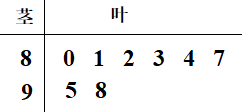(1)、求 $n$ 和频率分布直方图中的 $x ， y$ 的值；

(2)、根据样本估计总体的思想，以事件发生的频率作为相应事件发生的概率，若在该校高一学生任选3人，求至少有1人成绩是合格等级的概率；

(3)、在选取的样本中，从 $A 、 C$ 两个等级的学生中随机抽取了3名学生进行调研，记 $X$ 表示所抽取的3名学生中为 $C$ 等级的学生人数，求随机变量 $X$ 的分布列及数学期望.

查看试题解析
20. 已知椭圆 $C ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的焦距为4，其短轴的两个端点与长轴的一个端点构成正三角形.

(1)、求椭圆 $C$ 的标准方程；

(2)、设 $F$ 为椭圆 $C$ 的左焦点， $T$ 为直线 $x = - 3$ 上任意一点，过 $F$ 作 $T F$ 的垂线交椭圆 $C$ 于点 $P$ 和 $Q$ .试判断 $O T$ 是否平分线段 $P Q$ （其中 $O$ 为坐标原点），并求当 $\frac{| T F |}{| P Q |}$ 取最小值时点 $T$ 的坐标.

查看试题解析
21. 已知函数 $f (x) = x^{2} - (2 a + 1) x + a \ln x (a \in R)$ .

(1)、若 $f (x)$ 在区间 $[1 ， 2]$ 上是单调函数，求实数a的取值范围；

(2)、函数 $g (x) = (1 - a) x$ ，若 $\exists x_{0} \in [1 ， e]$ 使得 $f (x_{0}) \geq g (x_{0})$ 成立，求实数a的取值范围.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，已知点 $P (0, - \sqrt{3})$ ，曲线 $C$ 的参数方程为 ${\begin{matrix} x = 2 c o s φ \\ y = 2 s i n φ \end{matrix}$ ( $φ$ 为参数).以原点为极点， $x$ 轴非负半轴为极轴建立极坐标系，直线 $l$ 的极坐标方程为 $ρ c o s (θ + \frac{π}{3}) = \frac{3}{2}$ .

(1)、判断点 $P$ 与直线 $l$ 的位置关系并说明理由；

(2)、设直线 $l$ 与曲线 $C$ 交于 $A, B$ 两个不同的点，求 $\frac{1}{| P A |} + \frac{1}{| P B |}$ 的值.

查看试题解析
23. 已知函数 $f (x) = | 2 x + a | + | 2 x - b | + 2$ 的最小值为3.

(1)、求 $a + b$ 的值；

(2)、若 $a > 0 ， b > 0$ ，求证： $a + b \geq 3 - \log_{3} (\frac{4}{a} + \frac{1}{b})$ .

查看试题解析

百分制	85分及以上	70分到84分	60分到69分	60分以下
等级	$A$	$B$	$C$	$D$

$X$	$- 1$	0	1
$P$	$a$	$\frac{1}{3}$	$c$