山东省德州市夏津县2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 下列各式中是二次根式的为( )A、 B、 C、 D、2. 下列各组数中,以它们为边的三角形不是直角三角形的是A、1.5,2,3 B、7,24,25 C、6,8,10 D、3,4,53. 如果最简二次根式 与 能够合并,那么 的值为( ).
A、2 B、3 C、4 D、54. 如图,菱形ABCD中,∠B=120°,则∠1的度数是( ) A、30° B、25° C、20° D、15°5. 下列运算正确的是( )A、 B、 C、 D、6. 顺次连结任意四边形各边中点所得到的四边形一定是( )A、平行四边形 B、菱形 C、矩形 D、正方形7. 如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( )
A、30° B、25° C、20° D、15°5. 下列运算正确的是( )A、 B、 C、 D、6. 顺次连结任意四边形各边中点所得到的四边形一定是( )A、平行四边形 B、菱形 C、矩形 D、正方形7. 如图,将▱ABCD沿对角线AC折叠,使点B落在B′处,若∠1=∠2=44°,则∠B为( ) A、66° B、104° C、114° D、124°8. 如图,在平行四边形 中, 、 是 上两点, ,连接 、 、 、 ,添加一个条件,使四边形 是矩形,这个条件是( )
A、66° B、104° C、114° D、124°8. 如图,在平行四边形 中, 、 是 上两点, ,连接 、 、 、 ,添加一个条件,使四边形 是矩形,这个条件是( )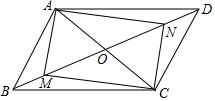 A、 B、 C、 D、9. 如图,在矩形 中,点B的坐标是 ,则 的长是( )
A、 B、 C、 D、9. 如图,在矩形 中,点B的坐标是 ,则 的长是( ) A、3 B、 C、 D、410. 如图,在长方形ABCD中,点E在边AB上,把长方形ABCD沿直线DE折叠,点A落在边BC上的点F处.若AE=5,BF=3.则△CDF的面积是( )
A、3 B、 C、 D、410. 如图,在长方形ABCD中,点E在边AB上,把长方形ABCD沿直线DE折叠,点A落在边BC上的点F处.若AE=5,BF=3.则△CDF的面积是( ) A、52 B、108 C、54 D、6011. 如图所示,已知圆柱的底面周长为36,高AB=5,P点位于圆周顶面处,小虫在圆柱侧面爬行,从A点爬到P点,然后再爬回C点,则小虫爬行的最短路程为( )
A、52 B、108 C、54 D、6011. 如图所示,已知圆柱的底面周长为36,高AB=5,P点位于圆周顶面处,小虫在圆柱侧面爬行,从A点爬到P点,然后再爬回C点,则小虫爬行的最短路程为( ) A、26 B、13+ C、13 D、212. 如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )
A、26 B、13+ C、13 D、212. 如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
13. 已知x,y为实数,且 , 则x+y+1= .14. 用任意两个全等的直角三角形拼下列图形:①平行四边形,②矩形,③菱形,④正方形,⑤等腰三角形,⑥等边三角形,其中一定能够拼成的图形是.(只填题号)15. 如图,在菱形ABCD中, , ,E,F分别是CD和BC的中点,连接EF并延长与AB的延长线相交于点G,则EG的长度为cm.
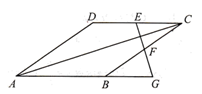 16. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.
16. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长=cm.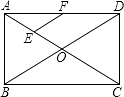 17. 正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为 .
17. 正方形ABCD的边长为4,点P在DC边上,且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为 . 18. 如图,在中, , . 将AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、……,则旋转得到的第2020个三角形的直角顶点的坐标为 .
18. 如图,在中, , . 将AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、……,则旋转得到的第2020个三角形的直角顶点的坐标为 .
三、解答题
-
19. 计算:(1)、;(2)、 .20. 如图,小红同学要测量A,C两地的距离,但A,C之间有一水池,不能直接测量,于是她在A,C同一水平面上选取了一点B,点B可直接到达A,C两地.她测量得到AB=80米,BC=20米,∠ABC=120°.请你帮助小红同学求出A,C两地之间的距离.(结果精确到1米,参考数据:≈4.6)
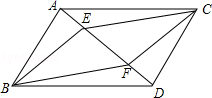
 21. 已知:如图,在平行四边形ABCD中,点E、F在AD上,且AE=DF
21. 已知:如图,在平行四边形ABCD中,点E、F在AD上,且AE=DF求证:四边形BECF是平行四边形.
 22. 勾股定理是一条古老的数学定理,它有很多种证明方法
22. 勾股定理是一条古老的数学定理,它有很多种证明方法
 (1)、请你根据图1填空;勾股定理成立的条件是三角形,结论是(三边关系)(2)、以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;23. 如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,
(1)、请你根据图1填空;勾股定理成立的条件是三角形,结论是(三边关系)(2)、以图1中的直角三角形为基础,可以构造出以a、b为底,以a+b为高的直角梯形(如图2),请你利用图2,验证勾股定理;23. 如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,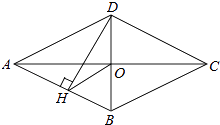 (1)、求证:∠DHO=∠DCO.(2)、若OC=4,BD=6,求菱形ABCD的周长和面积.
(1)、求证:∠DHO=∠DCO.(2)、若OC=4,BD=6,求菱形ABCD的周长和面积.
