山西省太原市2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $3^{0}$ 的结果是（）

A、3 B、1 C、0 D、 $\frac{1}{3}$

查看试题解析
2. 如图，将直尺与三角尺叠放在一起，直角顶点恰好在直尺的一边上，若∠1=25°，则 $∠ 2$ 的度数为（）

A、65° B、50° C、75° D、25°

查看试题解析
3. 下列计算正确的是（）

A、 ${(- a^{3})}^{2} = - a^{6}$ B、 $a^{3} \cdot a^{2} = a^{6}$ C、 ${(2 a)}^{2} = 2 a^{2}$ D、 $a^{3} \div a^{2} = a$

查看试题解析
4. 木工师傅用图中的角尺画平行线，他依据的数学道理是（）

A、同位角相等，两直线平行 B、内错角相等，两直线平行 C、两直线平行，同位角相等 D、两直线平行，内错角相等

查看试题解析
5. 下列多项式乘法中，不能用平方差公式计算的是（）

A、 $(x - y) (x + y)$ B、 $(- x + y) (x - y)$ C、 $(4 x^{2} - y^{2}) (4 x^{2} + y^{2})$ D、 $(3 x + 1) (1 - 3 x)$

查看试题解析
6. 目前，中国在硅基量子芯片制造上，获得了突破性进展，让两个磷原子的量子点实现了结合．一旦技术成熟，在芯片制造上 $1 n m = 1 0^{- 9} m$ ，则数据“ $13 n m$ ”用科学记数法表示为（）

A、 $13 \times 1 0^{9} m$ B、 $13 \times 1 0^{- 9} m$ C、 $1.3 \times 1 0^{- 10} m$ D、 $1.3 \times 1 0^{- 8} m$

查看试题解析
7. 梦想从学习开始，事业从实践起步近来，每天登录“学习强国”APP，则下列说法不正确的是（）
学习天数n（天）
1
2
3
4
5
6
7
周积分w/（分）
55
110
160
200
254
300
350

A、在这个变化过程中，学习天数是自变量，周积分是因变量 B、周积分随学习天数的增加而增加 C、周积分w与学习天数n的关系式为 $w = 50 n$ D、天数每增加1天，周积分的增长量不一定相同

查看试题解析
8. 某县积极推进“乡村振兴计划”，要对一段水渠进行扩建．如图，已知现有水渠从A地沿北偏东50°的方向到B地，从B村沿北偏西20°方向到C村．使CD $/ /$ AB，则 $∠ B C D$ 的度数为（）

A、50° B、70° C、110° D、130°

查看试题解析
9. 如图，已知 $∠ A O B$ ，点C在射线OB上．按下列步骤作图：①以O为圆心、OC长为半径画弧；②以C为圆心、CD长为半径画弧，交前面的弧于点E；④连接CD，CE．则下列结论不一定成立的是（）

A、 $∠ A O B = ∠ B O E$ B、 $C D = C E$ C、 $O D = O E$ D、 $C D = O D$

查看试题解析
10. 人的大脑所能记忆的内容是有限的，随着时间的推移，记忆的东西会逐渐被遗忘德国心理学家艾宾浩斯（HermannEbbinghaus，1850—1909）（如图），这就是非常有名的艾宾浩斯遗忘曲线，其中竖轴表示学习中的记忆保持量，横轴表示时间．分析图象得到下列结论（）

A、记忆后的1小时之内，遗忘速度最慢 B、记忆保持量下降到50%所用时间为4小时 C、点A表示记忆15小时后记忆保持量约为36% D、记忆12小时后，记忆保持量保持不变

查看试题解析

二、填空题

11. 计算 $2^{- 2}$ 的结果是．

查看试题解析
12. 若一个角和它的补角相等，则这个角的度数为．

查看试题解析
13. 今年两会期间，“碳中和”成为焦点已知某种树林每天可吸收的二氧化碳量y（千克）与树林面积x（亩）之间的关系式为 $y = 67 x$ 根据这一关系式，当此种树林面积为100亩时，每天可吸收二氧化碳千克．

查看试题解析
14. 已知 $a + b = 3$ ， $a^{2} - b^{2} = 5$ ，则 $a - b =$ ．

查看试题解析
15. 已知点B是线段AC上的一点，分别以线段AB，BC，得到如图所示的图形，其中 $A B = 2 a$ ， BC=2b，其中 $a < b$ ，请从下面A，B两题中任选一题作答选择题．
A．图中阴影部分的面积为（用含a，b的代数式表示）；
B．若图中阴影部分的面积比空白部分面积少16 $π$ ，则 $b - a$ 的值为．

查看试题解析
16. 已知：如图，在三角形ABC中， $C D ⊥ A B$ 于点D，连接DE，当 $∠ 1 + ∠ 2 = 90$ 时，求证：DE//BC．
证明：∵ $C D ⊥ A B$ （已知），
∴ $∠ A D C = 90 °$ （垂直的定义）．
∴ $∠ 1 +$ $= 90 °$ ，
∵ $∠ 1 + ∠ 2 = 90 °$ （已知），
∴ $= ∠ 2$ （依据1：），
∴ $D E / / B C$ （依据2：）．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(a^{2})}^{3} \cdot a^{4} \div {(- a)}^{8}$ ．

(2)、 $(x - 1) (x + 2)$ ．

(3)、 ${(2 x + 3)}^{2} - 4 x (x + 1)$ ．

(4)、 $199 \times 201 + 1$ （用乘法公式）．

查看试题解析
18. 如图，已知 $∠ A O B$ ，点P是OB边上的一点．在 $∠ A O B$ 的内部求作∠BPC=∠AOB．要求：尺规作图，不写作法，保留作图痕迹．

查看试题解析
19. 先化简再求值 $[(a + b) (a - b) + {(a - b)}^{2}] \div 2 a$ ，其中 $a = - 1$ ， $b = 2$ ．

查看试题解析
20. 小明家距离学校8千米．一天早晨，小明骑车上学途中自行车出现故障他于原地修车，车修好后小明离家的距离S（千米）与他所用的时间x（分钟）之间的关系．请根据图象解答下列问题：

(1)、小明骑行千米时，自行车出现故障；修车用了分钟；

(2)、自行车出现故障前小明骑行的平均速度为千米/分，修好车后骑行的平均速度为千米/分；

(3)、若自行车不发生故障小明一直按故障前的速度匀速骑行，与他实际所用时间相比将早到或晚到学校多少分钟？

查看试题解析

21. 劳动是财富的源泉，也是幸福的源泉．沈河区某中学对劳动教育进行积极探索和实践，创建学生劳动教育基地，让学生参与农耕劳作．如图，现计划利用校园围墙的一段MN（MN最长可用25m），用40m长的篱笆，围成一个长方形菜园ABCD．设AB的长为xm（7.2≤x＞20）．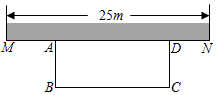

(1)、BC的长度为 m（用含x的代数式表示），长方形菜园的面积S（m²）与AB的长x（m）的关系式为S＝；

(2)、根据（1）中的关系式完成如表：

AB的长x（m）	8	9	10	11	12	13	14	15	……
菜园的面积S（m²）	192			198		182	168	150	……

(3)、请根据表中数据分析，S如何随x的变化而变化？（写出一个结论即可）

查看试题解析

22. 阅读下列材料，完成相应的任务：
三角形数古希腊著名的毕达哥拉斯学派把1，3，6，10，…，这样的数称为“三角形数” $\frac{n (n + 1)}{2}$ ；
任务：

(1)、第5个三角形数是；

(2)、请从下面A，B两题中任选一题作答．
A．智慧小组发现，①从第2个“三角形数”开始； $6 - 3 = 3$ ； $10 - 6 = 4$ ；；
②第 $n (n \geq 2)$ 个“三角形数”与第 $(n - 1)$ 个“三角形数”的差的规律可用下面的等式表示 $\frac{n (n + 1)}{2} - \frac{(n - 1) n}{2}$ = ．请补全该等式并说明它的正确性．
B．创新小组发现每相邻两个“三角形数”的和有一定的规律；如： $1 + 3 = 4$ ； $3 + 6 = 9$ ；①第5个“三角形数”与第6个“三角形数”的和为；②第n个“三角形数”与第 $(n + 1)$ 个“三角形数”的和的规律可用下面的等式表示：+= ．请补全该等式并说明它的正确性．

查看试题解析
23. 已知直线 $M N / / P Q$ ，点A在直线MN上，点B、C为平面内两点， $A C ⊥ B C$ 于点C．

(1)、如图1，当点B在直线MN上，点C在直线MN上方时，则 $∠ C A B$ 和 $∠ C D P$ 之间的数量关系是；

(2)、如图2，当点C在直线MN上且在点A左侧，点B在直线MN与PQ之间时，过点B $B D ⊥ A B$ 交直线PQ于点D，为探究 $∠ A B C$ 与 $∠ B D P$ 的数量关系，小明过点B作 $B F / / M N$ ，请根据他的思路，写出 $∠ A B C$ 与 $∠ B D P$ 的关系，并说明理由；

(3)、请从下面A，B两题中任选一题作答．
A 如图3，在（2）的条件下，作∠ABD的平分线交直线MN于点E，当 $∠ A E B = 2 ∠ A B C$ 时直接写出 $∠ A B C$ 的度数；
B 如图4，当点C在直线MN上且在点A左侧，点B在直线PQ下方时，过点B作 $B D ⊥ A B$ 交直线PQ于点D，作∠ABD的平分线交直线MN于点E，当 $∠ B D P = 2 ∠ B E N$ 时，直接写出 $∠ A B C$ 的度数．

查看试题解析

学习天数n（天）	1	2	3	4	5	6	7
周积分w/（分）	55	110	160	200	254	300	350