天津市南开区2020-2021学年七年级下学期期中数学试卷

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 在下列汽车标志的图案中，能用图形的平移来分析其形成过程的是（）

A、 B、 C、 D、

查看试题解析
2. 下列各数： $\frac{17}{3}$ ， $\sqrt{8}$ ， 2 ，0.333333， $\sqrt[3]{64}$ ， 1.21221222122221......（每两个1之间依次多一个 2），3.14， $2 - \sqrt{2}$ 中，无理数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
3. 下列生活中的实例，可以用“两点之间线段最短”来解释的是（）

A、把一根木条固定到墙上需要两颗钉子 B、从一条河道能向集镇引一条最短的水渠 C、小狗看到远处的食物，总是径直奔向食物 D、经过刨平木板上的两个点，能弹出一条笔直的墨线

查看试题解析
4. 如图，按各组角的位置判断不正确的是（）

A、∠1与∠4是同旁内角 B、∠3与∠4是内错角 C、∠5与∠6是同旁内角 D、∠2与∠5是同位角

查看试题解析
5. 8的立方根是（）

A、 4 B、 $- 4$ C、2 D、 $- 2$

查看试题解析
6. 已知 $\sqrt{a + 2} + | b - 1 | = 0$ ，那么 ${(a + b)}^{2017}$ 的值为（）

A、-1 B、1 C、 $3^{2017}$ D、 $- 3^{2017}$

查看试题解析
7. 当m为任意实数时，点A（m²＋1，－2）在第几象限（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 估计 $\sqrt{10} + 1$ 的值在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
9. 下列四个图形中，∠1与∠2是对顶角的是（）

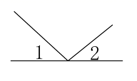A、 B、 C、 D、

查看试题解析
10. $\sqrt{3}$ ﹣2的绝对值是（）

A、2 $- \sqrt{3}$ B、 $\sqrt{3} - 2$ C、 $\sqrt{3}$ D、1

查看试题解析
11. 如图，∠1=70°，直线a平移后得到直线b，则∠2-∠3（）

A、70° B、180° C、110° D、80°

查看试题解析
12. 在平面直角坐标系中，对于点P（x，y），我们把点P'（﹣y+1，x+1）叫做点P伴随点已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得到点A₁ ， A₂A₃ ， …，An，…若点A₁的坐标为（2，4），点A₂₀₁₇的坐标为（）

A、（﹣3，3） B、（﹣2，﹣2） C、（3，﹣1） D、（2，4）

查看试题解析

二、填空题

13. 如图，在正方体中，与线段AB平行的线段有条．

查看试题解析
14. 已知 $\sqrt{23}$ 的整数部分为a，小数部分为b，则a-b=.

查看试题解析
15. 已知 $\sqrt{2.1}$ ＝1.449， $\sqrt{21}$ ＝4.573，则 $\sqrt{21000}$ 是．

查看试题解析
16. 把命题“等角的余角相等”改写成“如果…，那么…”的形式为．

查看试题解析
17. 如图，在△ABC 中，点 D 在边 AB 上，点 E，F 分别在边 AC 上，且满足 DF∥BE，DE∥BC，若∠ABC=46°，∠1=24°，则∠ADF 的度数是．

查看试题解析
18. 如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0）．现将线段AB向上平移2个单位，再向右平移1个单位，得到线段AB的对应线段CD，连接AC，BD．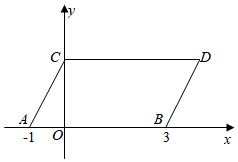

(1)、点D的坐标为；

(2)、在y轴上存在一点P，连接PA，PB，且S_△PAB＝2，求出满足条件的所有点P的坐标．

查看试题解析

三、解答题

19. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，△ABC的顶点都在格点上，建立平面直角坐标系.

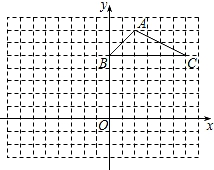(1)、点A的坐标为，点C的坐标为；

(2)、将△ABC先向左平移3个单位长度，再向下平移6个单位长度，请画出平移后的△A₁B₁C₁；

(3)、连接AB₁ ， B₁C，△AB₁C的面积＝.

查看试题解析
20. 在平面直角坐标系中，已知点P $(2 m + 4 ， m - 1)$ ，试分别根据下列条件，求出点P的坐标：

(1)、点P在 $y$ 轴上；

(2)、点P的纵坐标比横坐标大3；

(3)、点P到两坐标的距离相等；

(4)、点P在过A（2，-5）点，且与 $x$ 轴平行的直线上．

查看试题解析
21. 如图所示，已知∠DAB=∠DCB，AF平分∠DAB，CE平分∠DCB，∠FCE=∠CEB，试说明：AF∥CE．
解：因为∠DAB=∠DCB（                  ▲                  ），
又AF平分∠DAB，
所以                  ▲                  = $\frac{1}{2}$ ∠DAB（                  ▲                  ），
又因为CE平分∠DCB，
所以∠FCE=                  ▲                  （                  ▲                  ），
所以∠FAE=∠FCE．
因为∠FCE=∠CEB，
所以                  ▲                  =                  ▲
所以AF∥CE（                  ▲                  ）

查看试题解析
22.

(1)、化简 $| 1 - \sqrt{2} | + | \sqrt{2} - \sqrt{3} | + | \sqrt{3} - 2 |$ ．

(2)、计算： $\sqrt[3]{- 64} + \sqrt{16} \times \sqrt{\frac{9}{4}} \div (- \sqrt{2})^{2}$ ．

(3)、解方程（x﹣1）³＝27．

(4)、解方程2x²﹣50＝0．

查看试题解析
23. 在平面直角坐标系中，点A、B在坐标轴上，其中A(0， $a$ )、B( $b$ ，0)满足： $| 2 a - b - 1 | + \sqrt{a + 2 b - 8} = 0$

(1)、求A、B两点的坐标；

(2)、将线段AB平移到CD，点A的对应点为C(-2，t)，如图(1)所示．若三角形ABC的面积为9，求点D的坐标．

查看试题解析
24. 如图1，已知直线PQ∥MN，点A在直线PQ上，点C、D在直线MN上，连接AC、AD，∠PAC＝50°，∠ADC＝30°，AE平分∠PAD，CE平分∠ACD，AE与CE相交于E．

(1)、求∠AEC的度数；

(2)、若将图1中的线段AD沿MN向右平移到A₁D₁如图2所示位置，此时A₁E平分∠AA₁D₁ ， CE平分∠ACD₁ ， A₁E与CE相交于E，∠PAC＝50°，∠A₁D₁C＝30°，求∠A₁EC的度数．

(3)、若将图1中的线段AD沿MN向左平移到A₁D₁如图3所示位置，其他条件与（2）相同，求此时∠A₁EC的度数．

查看试题解析