天津市津南区2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 下列图形中,∠1与∠2是同旁内角的是( )A、
 B、
B、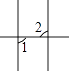 C、
C、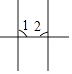 D、
D、 2. 下列图形中,线段PQ的长度表示点P到直线L的距离的是( )A、
2. 下列图形中,线段PQ的长度表示点P到直线L的距离的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
3. 如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )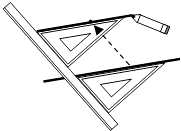 A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、两直线平行,同位角相等4. 下列句子中是命题且是真命题的是( )A、同位角相等 B、直线AB垂直CD吗 C、若a2=b2 , 则a=b D、同角的补角相等5. 估计的值在A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间6. 的算术平方根是( )A、 B、4 C、 D、27. 如果 , ,那么 约等于( ).A、 B、 C、 D、8. 在平面直角坐标系中,点 位于哪个象限?( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 在实数、、0、、3.1415、、、、6.1010010001…(相邻两个1之间的0依次增加1个)中,无理数的个数为( )A、3个 B、4个 C、5个 D、6个10. 若点P(x,y)的坐标满足xy=0(x≠y),则点P必在( )A、原点上 B、x轴上 C、y轴上 D、x轴上或y轴上(除原点)11. 已知点A在第二象限,到 x轴的距离是5,到y轴的距离是6,点A的坐标为( )A、 B、 C、 D、12. 在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )A、6,(﹣3,5) B、10,(3,﹣5) C、1,(3,4) D、3,(3,2)
A、同位角相等,两直线平行 B、内错角相等,两直线平行 C、同旁内角互补,两直线平行 D、两直线平行,同位角相等4. 下列句子中是命题且是真命题的是( )A、同位角相等 B、直线AB垂直CD吗 C、若a2=b2 , 则a=b D、同角的补角相等5. 估计的值在A、2到3之间 B、3到4之间 C、4到5之间 D、5到6之间6. 的算术平方根是( )A、 B、4 C、 D、27. 如果 , ,那么 约等于( ).A、 B、 C、 D、8. 在平面直角坐标系中,点 位于哪个象限?( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 在实数、、0、、3.1415、、、、6.1010010001…(相邻两个1之间的0依次增加1个)中,无理数的个数为( )A、3个 B、4个 C、5个 D、6个10. 若点P(x,y)的坐标满足xy=0(x≠y),则点P必在( )A、原点上 B、x轴上 C、y轴上 D、x轴上或y轴上(除原点)11. 已知点A在第二象限,到 x轴的距离是5,到y轴的距离是6,点A的坐标为( )A、 B、 C、 D、12. 在平面直角坐标系中,点A(﹣3,2),B(3,5),C(x,y),若AC∥x轴,则线段BC的最小值及此时点C的坐标分别为( )A、6,(﹣3,5) B、10,(3,﹣5) C、1,(3,4) D、3,(3,2)二、填空题
-
13. 如果用(7,8)表示七年级八班,那么八年级六班可表示成 .14. 矩形OABC在坐标系中的位置如图,点B坐标为(3,-2),则矩形的面积等于
 15. 已知直线m∥n,将一块含有30°角的三角板ABC按如图所示的方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上.若∠1=15°,则∠2= .
15. 已知直线m∥n,将一块含有30°角的三角板ABC按如图所示的方式放置(∠ABC=30°),其中A,B两点分别落在直线m,n上.若∠1=15°,则∠2= .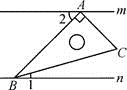 16. 如图,面积为3的正方形的顶点A在数轴上,且表示的数为1,若 , 则数轴上点E所表示的数为 .
16. 如图,面积为3的正方形的顶点A在数轴上,且表示的数为1,若 , 则数轴上点E所表示的数为 . 17. 如图,将△ABC沿BC方向平移1cm得到△DEF , 若△ABC的周长等于10cm , 则四边形ABFD的周长等于 .
17. 如图,将△ABC沿BC方向平移1cm得到△DEF , 若△ABC的周长等于10cm , 则四边形ABFD的周长等于 . 18. 若 ,则 .
18. 若 ,则 .三、解答题
-
19. 求下列各式中的值:(1)、;(2)、 .20. 计算:(1)、;(2)、 .21. 已知一个数 m 的两个不相等的平方根分别为 a+3 和 2a-15,(1)、求 a 的值.(2)、求这个数 m22. 如图,在平面直角坐标系中,△ABC的顶点都在网格点上,每个小正方形边长为1个单位长度.
 (1)、将△ABC向右平移6个单位,再向下平移3个单位得到△A1B1C1 , 画出图形,并写出各顶点坐标;(2)、求△ABC的面积.23. 如图, 交 于 , .
(1)、将△ABC向右平移6个单位,再向下平移3个单位得到△A1B1C1 , 画出图形,并写出各顶点坐标;(2)、求△ABC的面积.23. 如图, 交 于 , . (1)、若 ,求 的度数;(2)、若 ,求 的度数.24. 如图,已知AD⊥BC于D,FG⊥BC垂足分别为D,G,且∠1=∠2,∠C=50°,求∠EDC的度数.
(1)、若 ,求 的度数;(2)、若 ,求 的度数.24. 如图,已知AD⊥BC于D,FG⊥BC垂足分别为D,G,且∠1=∠2,∠C=50°,求∠EDC的度数.
证明:∵AD⊥BC,FG⊥BC,
∴∠ADC=∠FGC=90°( ▲ ).
∴ ▲ //FG( ▲ ).
∴∠1=∠3,
又∵∠1=∠2,
∴∠2=∠3( ▲ ).
∴DE// ▲ . ( ▲ ).
∴∠EDC+∠C=180°( ▲ ).
∵∠C=50°.
∴∠EDC= ▲ .

