山西省运城市盐湖区七校2020-2021学年七年级下学期期中联考数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $a^{- 3} \cdot (- a^{2})$ 的结果是（）

A、 $- a^{5}$ B、 $- a^{2}$ C、 $- \frac{1}{a}$ D、 $a^{- 5}$

查看试题解析
2. 如图，已知直线 $a / / b$ ，把三角尺的直角顶点放在直线b上．若 $∠ 1 = 40 °$ ，则 $∠ 2$ 的度数为（）

A、 $100 °$ B、 $110 °$ C、 $120 °$ D、 $130 °$

查看试题解析
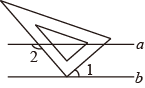3. 下列运算正确的是（）

A、 $x^{2} + x^{3} = x^{5}$ B、 $a^{6} \div a^{3} = a^{2}$ C、 ${(- 2 a^{2})}^{3} = - 8 a^{6}$ D、 $(a + b)^{2} = a^{2} + b^{2}$

查看试题解析
4. 如图，点P在直线l外，点A、B在直线l上，PA=4，PB＝7，则点P到直线l的距离可能是（）

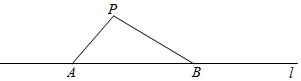A、3 B、4 C、5 D、7

查看试题解析
5. 下列说法正确的是（　　）

A、同位角相等 B、在同一平面内，如果a⊥b，b⊥c，则a⊥c C、相等的角是对顶角 D、在同一平面内，如果a∥b，b∥c，则a∥c

查看试题解析
6. 下列各式中，不能够用平方差公式计算的是（）

A、 $(2 y + x) (x - 2 y)$ B、 $(- x - 3 y) (x + 3 y)$ C、 $(2 x^{2} - y^{2}) (2 x^{2} + y^{2})$ D、 $(4 a + b - c) (4 a - b - c)$

查看试题解析
7. 在如图所示的四种沿AB进行折叠的方法中，不一定能判断纸带两条边a，b互相平行的是（　　）

A、如图1，展开后测得∠1=∠2 B、如图2，展开后测得∠1=∠2且∠3=∠4 C、如图3，测得∠1=∠2 D、在图④中，展开后测得∠1+∠2=180°

查看试题解析

8. 一个学习小组利用同一块木板，测量了小车从不同高度下滑的时间，他们得到如表数据：

支撑物的高度h(cm)	10	20	30	40	50	60	70	80	90	100
小车下滑的时间(s)	4.23	3.00	2.45	2.13	1.89	1.71	1.59	1.50	1.41	1.35

下列说法正确的是（）

A、当h=70cm时，t=1.50s B、h每增加10cm ， t减小1.23 C、随着h逐渐变大，也逐渐变大 D、随着h逐渐升高，小车下滑的平均速度逐渐加快

查看试题解析

9. 如图所示一块长方形的草地 $A B C D$ ，长 $A B = a$ 米，宽 $B C = b$ 米，A，B入口处一条小路宽为1米，两条小路汇合处宽为2米，其余为草坪，则草坪面积为（）

A、 $(a - 1) (b - 2)$ B、 $(a - 2) (b - 1)$ C、 $(a - 1) (b - 1)$ D、 $(a - 2) (b - 2)$

查看试题解析
10. 小明看到了一首诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还”，读完后，他想用图象描述这首诗的内容，如果用纵轴表示父亲与儿子行进中离家的距离，横轴表示父亲离家的时间，那么下列图象中大致符合这首诗含义的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 计算：若 $2^{x} = 3 ， 2^{y} = 5$ ，则 $2^{x - y} =$ ．

查看试题解析
12. 世界最大的单口径球面射电望远镜被誉为“中国天眼”，在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为0.00519秒．数据0.00519用科学记数法可以表示为．

查看试题解析
13. 一副直角三角板如图放置，点D在边 $B C$ 上，点F在 $A B$ 的延长线上， $A F / / D E ， ∠ A = ∠ D F E = 90 °$ ，则 $∠ F D B$ 的余角的度数为度．

查看试题解析
14. 已知 $a + b = 2$ ， $a b = - 1$ ，则 $(a - 2) (b - 2)$ ＝；

查看试题解析
15. 已知动点P以每秒 $2 c m$ 的速度沿图甲的边框按从 $B \to C \to D \to E \to F \to A$ 的路径移动，相应的 $△ A B P$ 的面积 $S (c m^{2})$ 与时间t（秒）之间的关系如图乙中的图象所示，其中 $A B = 6 c m$ ．当 $t =$ 时， $△ A B P$ 的面积是 $18 c m^{2}$ ．

查看试题解析

三、解答题

16. 计算：

(1)、 $(3.14 - π)^{0} - {(- \frac{1}{2})}^{- 3} - 0.12 5^{2020} \times 8^{2021}$ ；

(2)、 ${(- {2^{}}^{})}^{2} \div (3 m^{3} n^{4}) \cdot {(- \frac{1}{2} m^{})}^{3}$ ；

(3)、 $(x + 3) (2 x - 1) - (x + 2) (x - 2)$ ．

查看试题解析
17. 先化简，再求值：
$(2 x + y) (2 x - y) - (x - 2 y)^{2} + y (- 4 x + 5 y + 1)$ ，其中 $x = 2 ， y = 2009$ ．

查看试题解析
18. 完成下面的证明．
已知：如图， $∠ B A C$ 与 $∠ G C A$ 互补， $∠ 1 = ∠ 2$ ，
求证： $∠ E = ∠ F$ ．
证明：∵ $∠ B A C$ 与 $∠ G C A$ 互补，
即 $∠ B A C + ∠ G C A = 180 °$ ，（已知）
∴                  ▲                   $/ /$                   ▲                   ．（                  ▲                  ）
∴ $∠ B A C = ∠ A C D$ ．（                  ▲                  ）
又∵ $∠ 1 = ∠ 2$ ，（已知）
∴ $∠ B A C - ∠ 1 = ∠ A C D - ∠ 2$ ，
即 $∠ E A C = ∠ F C A$ ．（                  ▲                  ）
∴                  ▲                   $/ /$                   ▲                   ．（                  ▲                  ）
∴ $∠ E = ∠ F$ ．（                  ▲                  ）

查看试题解析
19. 作图题：已知∠ABC及AB上一点A，

(1)、过点A画AE⊥BC，垂足为点E，此时线段的长为点A到直线BC的距离．

(2)、尺规作图（不写作法，保留作图痕迹）在射线BC上，以C为定点，作∠FCD=∠ABC

查看试题解析
20. 如图，已知点E、F在直线 $A B$ 上，点G在线段 $C D$ 上， $E D$ 与 $F G$ 交于点H， $∠ C = ∠ E F G ， ∠ C E D = ∠ G H D$ ．

(1)、判断 $A B$ 与 $C D$ 的位置关系，并说明理由；

(2)、若 $∠ E H F = 80 ° ， ∠ D = 30 °$ ，求 $∠ A E M$ 的度数．

查看试题解析
21. “珍重生命，注意安全！”同学们在上下学途中一定要注意骑车安全．小明骑单车上学，当他骑了一段时，想起要买某本书，于是又折回到刚经过的新华书店，买到书后继续去学校，以下是他本次所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：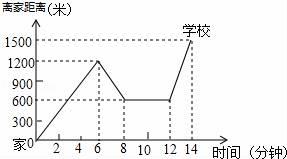

(1)、小明家到学校的路程是多少米？

(2)、小明在书店停留了多少分钟？

(3)、本次上学途中，小明一共行驶了多少米？一共用了多少分钟？

(4)、我们认为骑单车的速度超过300米/分钟就超越了安全限度．问：在整个上学的途中哪个时间段小明骑车速度最快，速度在安全限度内吗？

查看试题解析
22. 把几个图形拼成一个新的图形，再通过两种不同的方法计算同一个图形的面积，可以得到一个等式，也可以求出一些不规则图形的面积．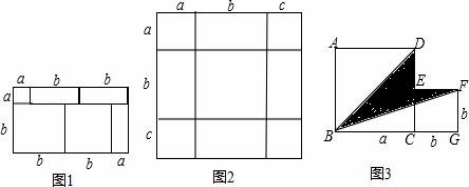

例如，由图1，可得等式：（a+2b）（a+b）=a²+3ab+2b²

(1)、如图2，将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形，试用不同的形式表示这个大正方形的面积，你能发现什么结论？请用等式表示出来．

(2)、利用（1）中所得到的结论，解决下面的问题：已知a+b+c=11，ab+bc+ac=38，求a²+b²+c²的值．

(3)、如图3，将两个边长分别为a和b的正方形拼在一起，B，C，G三点在同一直线上，连接BD和BF．若这两个正方形的边长满足a+b=10，ab=20，请求出阴影部分的面积．

查看试题解析
23. 如图，AB∥CD，定点E，F分别在直线AB，CD上，平行线AB，CD之间有一动点P．

(1)、如图1，当P点在EF的左侧时，∠AEP，∠EPF，∠PFC满足数量关系为，如图2，当P点在EF的右侧时，∠AEP，∠EPF，∠PFC满足数量关系为．

(2)、如图3，当∠EPF＝90°，FP平分∠EFC时，求证：EP平分∠AEF；

(3)、如图4，QE，QF分别平分∠PEB和∠PFD，且点P在EF左侧．
①若∠EPF＝60°，则∠EQF＝ ▲ ．
②猜想∠EPF与∠EQF的数量关系，并说明理由；

查看试题解析