山西省临汾市翼城县2020-2021学年七年级下学期期中考试数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 下列方程中是一元一次方程的是( )A、 B、 C、 D、2. 下列各项中,蕴含不等关系的是( )A、老师的年龄是你的年龄的2倍 B、小丽和小华一样高 C、明天可能下雨 D、是非负数3. 解方程 , 去括号正确的是( )A、 B、 C、 D、4. 某商品涨价30%后欲恢复原价,则必须下降的百分数约为( )A、20% B、21% C、22% D、23%5. 已知m<n,下列不等式成立的是( )A、 B、 C、 D、6. 如果是方程的一组解,那么代数式的值是( )A、8 B、5 C、2 D、07. 三元一次方程组消去一个未知数后,所得二元一次方程组是( )A、 B、 C、 D、8. 小明在某月的日历上圈出了三个数a、b、c,并求出了它们的和为39,则这三个数在日历中的排位位置不可能的是( )A、
 B、
B、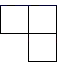 C、
C、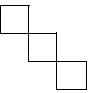 D、
D、 9. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、10. 已知关于 , 的二元一次方程组 , 给出下列结论中正确的是( )
9. 《孙子算经》是中国古代重要的数学著作,纸书大约在一千五百年前,其中一道题,原文是:“今三人共车,两车空;二人共车,九人步.问人与车各几何?”意思是:现有若干人和车,若每辆车乘坐3人,则空余两辆车:若每辆车乘坐2人,则有9人步行,问人与车各多少?设有x人,y辆车,可列方程组为( )A、 B、 C、 D、10. 已知关于 , 的二元一次方程组 , 给出下列结论中正确的是( )①当这个方程组的解 , 的值互为相反数时,;
②当时,方程组的解也是方程的解;
③无论取什么实数,的值始终不变;
④若用表示 , 则;
A、①② B、②③ C、②③④ D、①③④二、填空题
-
11. 已知方程 , 用含x的式子表示y,则 .12. 若与的是同类项,则 .13. 根据如图所示,用不等式表示公共部分的范围 .
 14. 2020年5月11日习总书记到山西大同云州区视察了有机黄花标准化种植基地,他指出要保护好、发展好这个产业,让黄花成为群众脱贫致富的“摇钱草”.黄花又名萱草、金针菜、忘忧草,是一种营养价值很高的蔬菜,从明朝开始,大同就享有“黄花之乡”的盛名,原价为70元/千克的黄花菜,每天可售出30千克,在试销时发现,售价每降 , 售出的黄花菜增加 , 现在每天销售这种黄花菜的总售价为2268元.根据题意,可列方程为: .
14. 2020年5月11日习总书记到山西大同云州区视察了有机黄花标准化种植基地,他指出要保护好、发展好这个产业,让黄花成为群众脱贫致富的“摇钱草”.黄花又名萱草、金针菜、忘忧草,是一种营养价值很高的蔬菜,从明朝开始,大同就享有“黄花之乡”的盛名,原价为70元/千克的黄花菜,每天可售出30千克,在试销时发现,售价每降 , 售出的黄花菜增加 , 现在每天销售这种黄花菜的总售价为2268元.根据题意,可列方程为: .
黄花菜喜光耐旱地,但花期需水量大,若遇干旱花蕾易脱落.其地上部分不耐寒,开花期要求较高温度,较为适宜.黄花菜对地形要求不高,地壤忌过湿或积水
15. 学校在“学党史、讲党史、感党恩”活动中,计划用750元购进《中国共产党简史》和《四史专题讲座》两书,《中国共产党简史》每本35元,《四史专题讲座》每本30元,有种购书方案.16. 如图,在数轴上,点A,B分别表示-15,9,点P,Q分别从点A,B同时开始沿数轴正方向运动,点P的速度是每秒3个单位,点Q的速度是每秒1个单位,运动时间为t秒.在运动过程中,当点P,点Q和原点O这三点中的一点恰好是另外两点为端点的线段的中点时,t的值是 .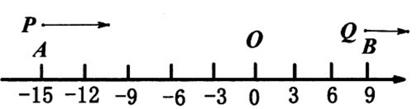
三、解答题
-
17. 解方程(1)、(2)、18. 小明、小丽两位同学在学习过程中遇到这样一个问题;二元一次方程组的解满足 , 求x、y、k的值.
解①+②得
③
将代入③得
解这个方程得:…

小明 小丽
可称先消去k
(1)、请你接着完成小明的过程;(2)、请你按照小丽同学的思路完成本题.19. 已知关于x的不等式 , 两边同除以 , 得 , 试化简: .20. 甲、乙两人共同解方程组 , 由于甲看错了方程①中的a,得到方程组的解为 , 乙看错了方程②中的b,得到方程组的解为 , 试计算的值.21. 我们称使方程成立的一对数x,y为“相伴数对”,记为 .(1)、若是“相伴数对”,求y的值;(2)、若是“相伴数对”,请用含q的代数式表示p;(3)、若是“相伴数对”,求代数式的值.22. 阅读下面材料,完成填空.你能比较两个数和的大小吗?
为了解决这个问题,先把问题一般化,既比较和的大小( , 且n为整数).然后从分析 , …这些简单情形入手,从中发现规律,经过归纳,猜想出结论.
(1)、通过计算,比较下列①、②、③、④各组两个数的大小(在横线上填>、=、<号)①;②;③;④;⑤;⑥;⑦;…
(2)、从第(1)小题的结果经过归纳,可以猜想出和的大小关系.(3)、根据上面归纳猜想得到的一般结论,可以得到(填>、=、<号).23. 聪聪与明明分别要把两块边长都为的正方形薄钢片要制作成两个无盖的长方体盒子(不计粘合部分).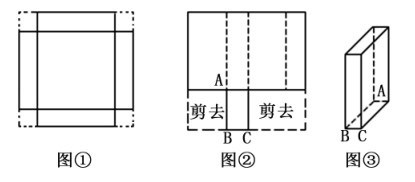 (1)、聪聪先在薄钢片四个角截去边长为的四个相同的小正方形(如图①),然后把四边折合粘在一起,便得到甲种盒子,请你帮忙求出该种盒子底面边长;(2)、明明截去两角后(如图②),沿虚线折合粘在一起,便得到乙种盒子(如图③),已知乙种盒子底面的长是宽的2倍,求乙种盒子底面的长与宽分别是多少?(3)、若把乙种盒子装满水后,倒入甲种盒子内,问是否可以装满甲种盒子,若能装满甲种盒子,那么乙种盒子里的水面有多高?若不能装满甲种盒子,求出此甲种盒子的水面的高度.24. 有些关于方程组的问题,需要求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:
(1)、聪聪先在薄钢片四个角截去边长为的四个相同的小正方形(如图①),然后把四边折合粘在一起,便得到甲种盒子,请你帮忙求出该种盒子底面边长;(2)、明明截去两角后(如图②),沿虚线折合粘在一起,便得到乙种盒子(如图③),已知乙种盒子底面的长是宽的2倍,求乙种盒子底面的长与宽分别是多少?(3)、若把乙种盒子装满水后,倒入甲种盒子内,问是否可以装满甲种盒子,若能装满甲种盒子,那么乙种盒子里的水面有多高?若不能装满甲种盒子,求出此甲种盒子的水面的高度.24. 有些关于方程组的问题,需要求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:已知实数x,y满足①,②,求和的值.
本题常规思路是将①②两式联立组成方程组,解得x,y的值再代入欲求值的代数式得到答案,常规思路运算量比较大.其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①-②可得 , 由①+②×2可得 . 这样的解题思想就是通常所说的整体思想.
解决问题:
(1)、已知二元一次方程组 , 则 , ;(2)、“战疫情,我们在一起”,爱心公社计划为老年公寓捐赠一批防疫物资.已知购买20瓶消毒液、3支测温枪、2套防护服共需1180元;购买30瓶消毒液、2支测温枪、8套防护服共需2170元,若该公益组织实际捐赠了100瓶消毒液、10支测温枪、20套防护服,则购买这批防疫物资共需多少元?(3)、对于实数x,y,定义新运算: , 其中a,b,c是常数,等式右边是通常的加法和乘法运算.已知 , 那么求的值.