山西省临汾市尧都区2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 方程x﹣2=2﹣x的解是（　　）

A、x=1 B、x=﹣1 C、x=2 D、x=0

查看试题解析
2. 已知a＞b，则下列结论不正确的是（）

A、a+2＞b+2 B、﹣a＜﹣b C、a﹣3＞b﹣3 D、1﹣2a＞1﹣2b

查看试题解析
3. 一元一次方程 $\frac{2 x - 1}{3} - \frac{5 x + 2}{6} = 2$ ，去分母后变形正确的是（）

A、 $4 x - 2 - 5 x + 2 = 2$ B、 $4 x - 2 - 5 x - 2 = 2$ C、 $4 x - 2 - 5 x + 2 = 12$ D、 $4 x - 2 - 5 x - 2 = 12$

查看试题解析
4. 将不等式的解集x≥﹣2表示在数轴上，正确的是（）

A、 B、 C、 D、

查看试题解析
5. 已知方程组 ${\begin{array}{l} 2 x + 3 y = 14 \\ x + 4 y = 12 \end{array}$ ，则 $x - y$ 的值是（）

A、1 B、2 C、4 D、5

查看试题解析
6. 你知道吗？现在世界上最古老的方程出现在英国考古学家莱茵德1858年找到的一份古埃及人的“纸草书”上．在我国，“方程”一词最早出现于东汉初年的一部数学著作中，这部著作的名称是（）

A、《周髀算经》 B、《九章算术》 C、《五经算术》 D、《孙子算经》

查看试题解析
7. 若不等式（m+1）x＞m+1的解集为x＜1，则m满足的条件是（）

A、m＜﹣1 B、m＞0 C、m＜0 D、m≥﹣1

查看试题解析
8. 小华告诉小明：我生日的月数和日数之和为24，且日数恰好是月数的7倍，你猜我的生日是哪天？小华的生日应该是（）

A、3月21日 B、2月14日 C、8月16日 D、4月24日

查看试题解析
9. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”意思是：用一根绳子去量一根木条，绳子还剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?如果设木条长x尺，绳子长y尺，那么可列方程组为（）

A、 ${\begin{cases} y = x + 4.5 \\ 0.5 y = x - 1 \end{cases}$ B、 ${\begin{cases} y = x + 4.5 \\ y = 2 x - 1 \end{cases}$ C、 ${\begin{cases} y = x - 4.5 \\ 0.5 y = x + 1 \end{cases}$ D、 ${\begin{cases} y = x - 4.5 \\ y = 2 x - 1 \end{cases}$

查看试题解析
10. 在数学活动课上，兴趣小组的同学们用4块大小不同的长方形纸板和一块小正方形纸板拼成了一个大正方形，有关数据如图所示，则拼成的大正方形的面积是（）

A、20 B、25 C、36 D、49

查看试题解析

二、填空题

11. 写出一个二元一次方程，使它的解为 ${\begin{cases} x = 2 \\ y = - 3 \end{cases}$ ，方程：．

查看试题解析
12. 周末，丽丽的妈妈买了她爱吃的菠萝和香蕉，丽丽上网查找得到：菠萝适宜的冷藏温度是7℃﹣13℃，香蕉适宜的冷藏温度是11℃﹣15℃，现在要将菠萝和香蕉同时放在一起冷藏，则冰箱应设置的适宜温度是．

查看试题解析
13. 新定义一种运算符号“△”，规定x△y＝xy+x²﹣3y，已知2△m＝6，则m的值为．

查看试题解析
14. 已知关于x的不等式组 ${\begin{array}{l} 2 x - 3 \leq 1 \\ x - a > 0 \end{array}$ 有且只有4个整数解，则a的取值范围是．

查看试题解析
15. 21年4月4日，双语实验学校组织全校师生前往烈士陵园，开展缅怀革命先烈，传承红色精神的主题活动．已知队伍全长450米，以90米/分的速度匀速前进．王平同学要从排尾到排头取东西，并立即返回排尾，且速度为180米/分．则他往返共需分钟．

查看试题解析

三、解答题

16.

(1)、解方程组： ${\begin{array}{l} 5 x + y = 7 \\ 3 x - y = 1 \end{array}$ ．

(2)、解不等式组： ${\begin{array}{l} 3 (x - 2) \leq x - 4 \\ 2 x - 3 < 3 x - 1 \end{array}$ ．

查看试题解析
17. 下面是王丽解方程 $\frac{2 x - 1}{4} = 1 - \frac{3 - x}{8}$ 的过程：
解：去分母得：2（2x﹣1）＝8﹣（3﹣x）（第一步），
去括号得：4x﹣2＝5﹣x（第二步），
移项合并得：5x＝7（第三步），
系数化为1得：x＝ $\frac{7}{5}$ （第四步），
根据解答过程完成下列任务．

(1)、任务一：①上述解答过程中，第一步的变形依据是；②第步开始出现错误，这一步不正确的原因是；

(2)、任务二：方程正确的解为；

(3)、任务三：请你根据平时解一元一次方程的经验，再给其他同学提一条建议．

查看试题解析
18. 小丽的练习册上有一道解方程题目，其中一个数字处恰好有一个三角形小洞，变成了 $\frac{x - Δ}{5} + \frac{3 x - 2}{10} = \frac{2 x + 1}{3}$ ，她查看了后面的答案后，得知该方程的解为x＝﹣8，请你帮小丽把这个小洞处的数字补上．

查看试题解析
19. 已知关于x，y的二元一次方程组 ${\begin{array}{l} 2 x - y = 4 m + 3 \\ 2 y - x = - 3 \end{array}$ 的解x，y互为相反数．求m²﹣2m+1的值．

查看试题解析
20. 小红和小明是好朋友，小红每天步行上学且所需时间保持不变．小明骑自行车或步行上学，骑自行车速度为240米/分，步行速度为80米/分．下面是两人的对话，请根据对话内容计算：小明从家到学校的路程和小红从家到学校的时间．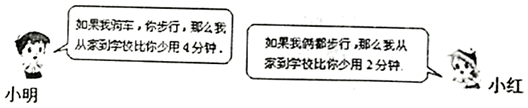

查看试题解析
21. 阅读理解：
已知a，b为有理数，且a≠0，若关于x的一元一次方程ax＝b的解为x＝b+a，我们就定义该方程为“和解方程”．
例如：方程2x＝﹣4的解为x＝﹣2，因为﹣2＝﹣4+2，所以方程2x＝﹣4是“和解方程”．请根据上述定义解答下列问题：

(1)、方程3x＝﹣6 “和解方程”；（填“是”或“不是”）

(2)、已知关于x的一元一次方程5x＝m是“和解方程”，求m的值；

(3)、已知关于x的一元一次方程4x＝ab+b是“和解方程”，且它的解是x＝b，则a，b的值分别为，．

查看试题解析
22. 网购已经成为人们喜欢的购物方式，为了“助农增收，精准扶贫”，临汾市电视台携手直播平台搞了“直播带货”活动．将我市的部分农产品推向网络．已知购买2袋浮山小米、3袋永和红枣，共需145元；购买1袋浮山小米、2袋永和红枣，共需90元．

(1)、求每袋浮山小米和每袋永和红枣各多少元？

(2)、某公司根据实际情况，决定购买浮山小米和永和红枣共100袋，要求购买总费用不超过3000元，那么应至少购买多少袋浮山小米？

查看试题解析
23. 综合与实践：
问题情境：我们知道：任何一个二元一次方程都有无数个解，但在实际问题中，我们常常只需要知道二元一次方程的正整数解即可，数学课上，王老师给出如下问题：有12个同学去公园划船，共有两种型号的船只，小船一只可乘2人，大船一只可乘3人，若同时租用两种船只，问应租用几只小船，几只大船？
思路引导：设需要x只小船，y只大船，由题意可得：2x+3y＝12，只要找到这个二元一次方程的正整数解即可．
解法示范：设需要x只小船，y只大船，由题意可得：2x+3y＝12，
∴ $x = \frac{12 - 3 y}{2}$ ，
∵x，y均为正整数，
∴ ${\begin{array}{l} y > 0 \\ 12 - 3 y > 0 \end{array}$ ，解得：0＜y＜4，
又∵ $x = \frac{12 - 3 y}{2}$ 为正整数，
∴y只能为2的倍数，
∴y＝2，代入得x＝3，
∴方程2x+3y＝12的正整数解为 ${\begin{array}{l} x = 3 \\ y = 2 \end{array}$ ，即应租用3只小船，2只大船．
理解运用：

(1)、请你写出方程2x+y＝5的所有正整数解；

(2)、果农王大叔有苹果25吨，计划同时租用A、B两种型号的货运车一次运送到冷库保存，且每辆车都载满已知1辆A型车一次可运3吨，1辆B型车一次可运4吨．
①请你帮王大叔设计所有可能的租车方案；
②若1辆A型车的租金为100元/次，1辆B型车的租金为120元/次，请选出费用最少的租车方案，并求出最少租车费．

查看试题解析