山西省晋中市介休市2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 计算的结果是( )A、 B、 C、 D、2. 两条直线被第三条直线所截,就第三条直线上的两个交点而言形成了“三线八角”.为了便于记忆,同学们可仿照图用双手表示“三线八角”(两大拇指代表被截直线,食指代表截线).下列三幅图依次表示( )
 A、同位角、同旁内角、内错角 B、同位角、内错角、同旁内角 C、同位角、对顶角、同旁内角 D、同位角、内错角、对顶角3. 下列计算正确的是( )A、 B、 C、 D、4. 将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是( )A、
A、同位角、同旁内角、内错角 B、同位角、内错角、同旁内角 C、同位角、对顶角、同旁内角 D、同位角、内错角、对顶角3. 下列计算正确的是( )A、 B、 C、 D、4. 将一副三角尺按不同位置摆放,下列摆放中∠1与∠2互为余角的是( )A、 B、
B、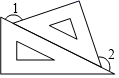 C、
C、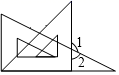 D、
D、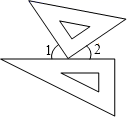 5. 绿色植物靠吸收光量子来进行光合作用,已知每个光量子的波长约为688纳米,1纳米=0.000 000 001米,则每个光量子的波长可用科学记数法表示为( )米A、 B、 C、 D、6. 如图,点E在 的延长线上,下列条件不能判断 的是( )
5. 绿色植物靠吸收光量子来进行光合作用,已知每个光量子的波长约为688纳米,1纳米=0.000 000 001米,则每个光量子的波长可用科学记数法表示为( )米A、 B、 C、 D、6. 如图,点E在 的延长线上,下列条件不能判断 的是( )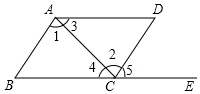 A、 B、 C、 D、7. 如图,点C在∠AOB的OB边上,用尺规作出了∠NCE=∠AOD,作图痕迹中,弧FG是( )
A、 B、 C、 D、7. 如图,点C在∠AOB的OB边上,用尺规作出了∠NCE=∠AOD,作图痕迹中,弧FG是( )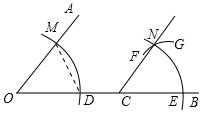 A、以点C为圆心,OD为半径的弧 B、以点C为圆心,DM为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DM为半径的弧8. 如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2的度数是( )
A、以点C为圆心,OD为半径的弧 B、以点C为圆心,DM为半径的弧 C、以点E为圆心,OD为半径的弧 D、以点E为圆心,DM为半径的弧8. 如图,将三个同样的正方形的一个顶点重合放置,如果∠1=45°,∠3=30°时,那么∠2的度数是( )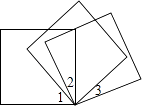 A、15° B、25° C、30° D、45°9. 综合与实践课上,小颖将长方形硬纸片的四个角处剪去边长为x的小正方形,再按折痕(虚线)折叠,可以制成有底无盖的长方体盒子,根据图中信息,该长方体盒子的体积可表示为:( )
A、15° B、25° C、30° D、45°9. 综合与实践课上,小颖将长方形硬纸片的四个角处剪去边长为x的小正方形,再按折痕(虚线)折叠,可以制成有底无盖的长方体盒子,根据图中信息,该长方体盒子的体积可表示为:( )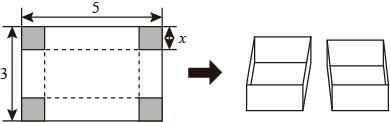 A、 B、 C、 D、10. 大家知道乌鸦喝水的故事,如图,它看到一个水位较低的瓶子,喝不着水,沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.从乌鸦看到瓶子的那刻起开始计时,设时间变量为 ,水位高度变量为 ,下列图象中最符合故事情景的大致图象是( )
A、 B、 C、 D、10. 大家知道乌鸦喝水的故事,如图,它看到一个水位较低的瓶子,喝不着水,沉思一会后聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,乌鸦喝到了水.从乌鸦看到瓶子的那刻起开始计时,设时间变量为 ,水位高度变量为 ,下列图象中最符合故事情景的大致图象是( ) A、
A、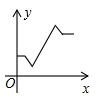 B、
B、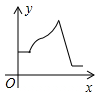 C、
C、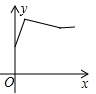 D、
D、
二、填空题
-
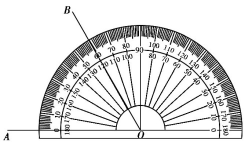
11. 已知: , , 则 .12. ∠AOB的大小可由量角器测得(如图所示),则∠AOB的补角的大小为.
 13. 如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=°.
13. 如图,直线a∥b,∠BAC的顶点A在直线a上,且∠BAC=100°.若∠1=34°,则∠2=°.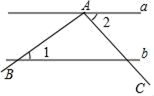 14. 某道路安装的护栏平面示意图如图所示,每根立柱宽为0.2米,立柱间距为3米,设有x根立柱,护栏总长度为y米,则y与x之间的关系式为.
14. 某道路安装的护栏平面示意图如图所示,每根立柱宽为0.2米,立柱间距为3米,设有x根立柱,护栏总长度为y米,则y与x之间的关系式为. 15. 如图,边长为的正方形纸片剪出一个边长为的正方形之后,剩余部分可剪拼成一个长方形,则这个长方形的周长为 .
15. 如图,边长为的正方形纸片剪出一个边长为的正方形之后,剩余部分可剪拼成一个长方形,则这个长方形的周长为 .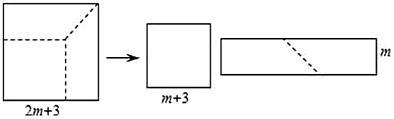
三、解答题
-
16. 计算:(1)、(2)、17. 先化简,再求值:(1)、 , 其中;(2)、 , 其中 , .18. 阅读下列证明过程,并完成任务:
如图,已知 , , .求证: .

证明:∵ , (已知),
∴ , (垂直的定义),
∴(等量代换),
∴(依据1),
∴(依据2),
……
任务:
(1)、上述解答过程中的“依据1”“依据2”分别指什么?“依据1”: .
“依据2”: .
(2)、将上述证明过程补充完整,并填写出每步的数学依据.19. 作图题:(1)、【画图并思考】:(不写作法,说明知识原理)如图,某村庄计划把河中的水引到水池中,怎样开渠线路最短,画出图形;其数学原理是.
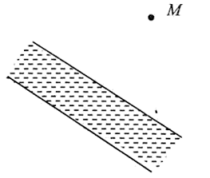 (2)、【尺规作图】:(不写作法,保留作图痕迹)
(2)、【尺规作图】:(不写作法,保留作图痕迹)已知:和如下图所示,画出 .
 20. 某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):
20. 某公交车每月的支出费用为4000元,每月的乘车人数x(人)与每月利润(利润=收入费用﹣支出费用)y(元)的变化关系如下表所示(每位乘客的公交票价是固定不变的):x(人)
500
1000
1500
2000
2500
3000
…
y(元)
﹣3000
﹣2000
﹣1000
0
1000
2000
…
(1)、在这个变化过程中,是自变量,是因变量;(2)、观察表中数据可知,每月乘客量达到人以上时,该公交车才不会亏损;(3)、请你估计当每月乘车人数为3500人时,每月利润为多少元?21. 如图1,有A型、B型正方形卡片和C型长方形卡片各若干张.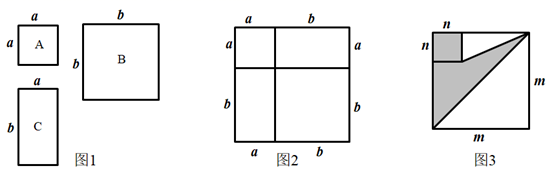 (1)、用1张A型卡片,1张B型卡片,2张C型卡片拼成一个正方形,如图2,用两种方法计算这个正方形面积,可以得到一个等式,请你写出这个等式;(2)、选取1张A型卡片,10张C型卡片,张B型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的代数式表示为;(3)、如图3,两个正方形边长分别为m、n,m+n=10,mn=19,求阴影部分的面积.22. “龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)、用1张A型卡片,1张B型卡片,2张C型卡片拼成一个正方形,如图2,用两种方法计算这个正方形面积,可以得到一个等式,请你写出这个等式;(2)、选取1张A型卡片,10张C型卡片,张B型卡片,可以拼成一个正方形,这个正方形的边长用含a,b的代数式表示为;(3)、如图3,两个正方形边长分别为m、n,m+n=10,mn=19,求阴影部分的面积.22. “龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑”时路程与时间的关系,请你根据图中给出的信息,解决下列问题.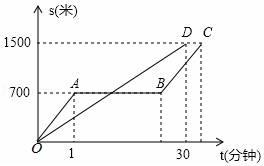 (1)、填空:折线OABC表示赛跑过程中的路程与时间的关系,线段OD表示赛跑过程中的路程与时间的关系.赛跑的全程是米.(2)、兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)、乌龟用了多少分钟追上了正在睡觉的兔子?(4)、兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?23. 综合与实践:
(1)、填空:折线OABC表示赛跑过程中的路程与时间的关系,线段OD表示赛跑过程中的路程与时间的关系.赛跑的全程是米.(2)、兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?(3)、乌龟用了多少分钟追上了正在睡觉的兔子?(4)、兔子醒来,以48千米/时的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟?23. 综合与实践:问题情境:将一副三角板中的两块直角三角尺的直角顶点按如图方式叠放在一起.
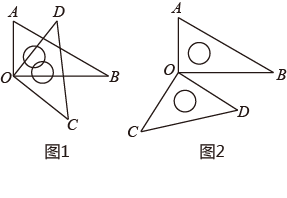 (1)、操作计算:
(1)、操作计算:如图(1),若 , 则;若 , 则;(直接写出结论即可)
(2)、类比探索:如图(2),若 , 则;(直接写出结论即可)
猜想验证:
(3)、猜想与的大小关系,并结合图(1)说明理由;(4)、拓展延伸:三角尺不动,将三角尺的边与边重合,然后绕点按顺时针或逆时针方向任意转动一个角度,当锐角等于多少度时,这两块三角尺各有一条边互相垂直,直接写出角度所有可能的值,不用说明理由.