内蒙古呼和浩特市回民区2020-2021学年七年级下学期期中考试数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 在中,已知 , , 则它的周长是( )A、 B、 C、 D、2. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、3. 下列各式计算正确的是( )A、 B、 C、 D、4. 在四边形中,对角线与相交于点给出下列四组条件:① , ;② , ;③ , ;④ , . 其中能判定这个四边形是平行四边形的条件有( )A、组 B、组 C、组 D、组5. 如图,菱形中,对角线相交于点O,E为边中点,菱形的周长为28,则的长等于( )
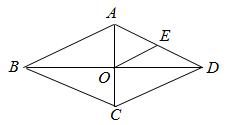 A、3.5 B、4 C、7 D、146. 如图,所有的三角形都是直角三角形,所有的四边形都是正方形,已知 , , , , 则的值是( )
A、3.5 B、4 C、7 D、146. 如图,所有的三角形都是直角三角形,所有的四边形都是正方形,已知 , , , , 则的值是( )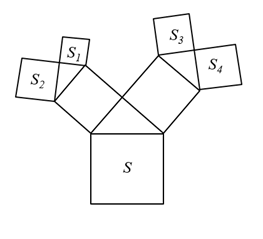 A、 B、 C、 D、7. 如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )
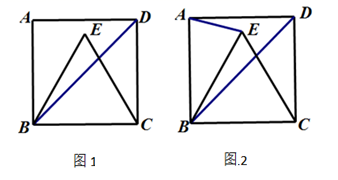
A、 B、 C、 D、7. 如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是( )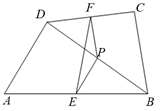 A、50° B、40° C、30° D、20°8. 若 , 则化简的结果为( )A、 B、3 C、 D、9. 如图,正方形ABCD和正方形CEFG,点G在CD上,AB=5,CE=2,T为AF的中点,则CT的长是( )
A、50° B、40° C、30° D、20°8. 若 , 则化简的结果为( )A、 B、3 C、 D、9. 如图,正方形ABCD和正方形CEFG,点G在CD上,AB=5,CE=2,T为AF的中点,则CT的长是( ) A、 B、4 C、 D、10. 如图,在平行四边形 中,对角线 , 交于点 , , , , 分别是 , , 的中点, 交 于点 . 则下列结论:① ;② ;③ ;④ , 其中成立的个数有( )
A、 B、4 C、 D、10. 如图,在平行四边形 中,对角线 , 交于点 , , , , 分别是 , , 的中点, 交 于点 . 则下列结论:① ;② ;③ ;④ , 其中成立的个数有( )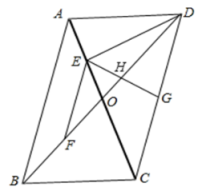 A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题
-
11. 若二次根式 在实数范围内有意义,则x的取值范围是 .
12. 若△ABC的三边长分别为a,b,c.下列条件:①∠A=∠B﹣∠C;②a2=(b+c)(b﹣c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13.其中能判断△ABC是直角三角形的是(填序号).13. 如图,每个小正方形的边长都相等, , , 是小正方形的顶点,则的度数为 .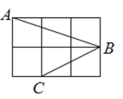 14. 若一个长方形的面积是 , 它的长与宽的比为 , 则它的长为 , 宽为 .15. 如图,以数轴的单位长度线段为边长作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是 .
14. 若一个长方形的面积是 , 它的长与宽的比为 , 则它的长为 , 宽为 .15. 如图,以数轴的单位长度线段为边长作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是 .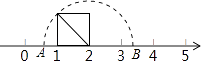 16. 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是以OD为腰的等腰三角形时,则P点的坐标为.
16. 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是以OD为腰的等腰三角形时,则P点的坐标为.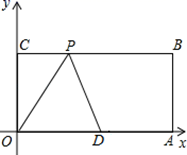
三、解答题
-
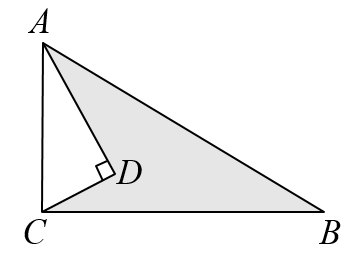
17. 计算:(1)、;(2)、 .18. 如图,已知 , , , , , 求图中阴影部分的面积.
 19. 如图,在 中, 于 , 于 ,连接 , .求证:四边形 是平行四边形.
19. 如图,在 中, 于 , 于 ,连接 , .求证:四边形 是平行四边形.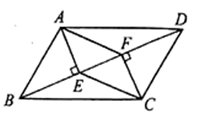 20. 如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m
20. 如图,一架长2.5m的梯子AB斜靠在墙AC上,∠C=90°,此时,梯子的底端B离墙底C的距离BC为0.7m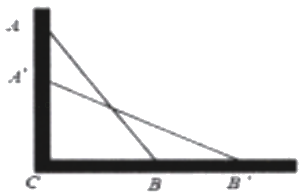 (1)、求此时梯子的顶端A距地面的高度AC;(2)、如果梯子的顶端A下滑了0.9m,那么梯子的底端B在水平方向上向右滑动了多远?21. 如图,在矩形中,厘米,厘米,点P从点D出发向点A运动,运动到点A即停止:同时点Q从点B出发向点C运动,运动到点C即停止,点P,Q的速度都是1厘米/秒.联结 . 设点P,Q运动时间为t秒.
(1)、求此时梯子的顶端A距地面的高度AC;(2)、如果梯子的顶端A下滑了0.9m,那么梯子的底端B在水平方向上向右滑动了多远?21. 如图,在矩形中,厘米,厘米,点P从点D出发向点A运动,运动到点A即停止:同时点Q从点B出发向点C运动,运动到点C即停止,点P,Q的速度都是1厘米/秒.联结 . 设点P,Q运动时间为t秒.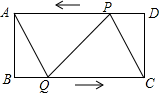 (1)、求当t为何值时,四边形是矩形;(2)、求当t为何值时,四边形是菱形.
(1)、求当t为何值时,四边形是矩形;(2)、求当t为何值时,四边形是菱形.