河北省衡水市阜城县2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $2 x^{2} \cdot (- 3 x^{3})$ 的结果是（）

A、 $- 6 x^{5}$ B、 $6 x^{5}$ C、 $- 6 x^{6}$ D、 $6 x^{6}$

查看试题解析
2. 已知如图①～④，其中 $∠ 1$ 与 $∠ 2$ 是同位角的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 已知一个二元一次方程组的解是 ${\begin{matrix} x = - 1 \\ y = - 2 \end{matrix}$ 则这个二元一次方程组可能是（）

A、 ${\begin{matrix} x + y = - 3 \\ x y = 2 \end{matrix}$ B、 ${\begin{matrix} x + y = - 3 \\ x - 2 y = 1 \end{matrix}$ C、 ${\begin{matrix} 2 x = y \\ x + y = - 3 \end{matrix}$ D、 ${\begin{matrix} x + y = 0 \\ 3 x - y = 5 \end{matrix}$

查看试题解析
4. 下列四根木棒中，能与 $5 c m$ ， $8 c m$ 长的两根木棒钉成一个三角形的是（）

A、 $3 c m$ B、 $8 c m$ C、 $13 c m$ D、 $15 c m$

查看试题解析
5. 下列式子：① $4 > 0$ ；② $2 x + 3 y < 0$ ；③ $x = 3$ ；④ $x + 3 ≤ 7$ ；⑤ $x + y$ 中，不等式的个数有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
6. 下列各式中，不能用平方差公式计算的是（）

A、（x-y）（-x+y） B、（-x+y）（-x-y） C、（-x-y）（x-y） D、（x+y）（-x+y）

查看试题解析
7. 利用加减消元法解方程组 ${\begin{array}{l} 2 x + 5 y = - 10 \\ 5 x - 3 y = 6 \end{array} \begin{array}{l} ① \\ ② \end{array}$ ，下列做法正确的是（）

A、要消去 $y$ ，可以将 $① \times 5 + ② \times 2$ B、要消去 $x$ ，可以将 $① \times 3 + ② \times (- 5)$ C、要消去 $y$ ，可以将 $① \times 5 + ② \times 3$ D、要消去 $x$ ，可以将 $① \times (- 5) + ② \times 2$

查看试题解析
8. 如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处，若∠A=26°，则∠CDE度数为（　　）．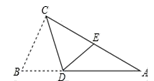

A、45°； B、64° ； C、71°； D、80°．

查看试题解析
9. 如图所示，8块相同的小长方形地砖拼成一个大长方形，若其中每一个小长方形的长为x，宽为y，则依据题意可得二元一次方程组为（）

A、 ${\begin{array}{l} x + y = 15 \\ x = 3 y \end{array}$ B、 ${\begin{array}{l} x + y = 15 \\ 2 x = 3 y \end{array}$ C、 ${\begin{array}{l} x - y = 15 \\ 2 x = x + 3 y \end{array}$ D、 ${\begin{array}{l} 2 x - y = 15 \\ 2 x = x + 3 y \end{array}$

查看试题解析
10. 如图，长方形ABCD的长为6，宽为4，将长方形先向上平移2个单位，再向右平移2个单位得到长方形 $A^{'} B^{'} C^{'} D^{'}$ ，则阴影部分面积是（）

A、12 B、10 C、8 D、6

查看试题解析
11. 下列命题中，真命题的个数是（）；①如果两条直线都与第三条直线平行，那么这两条直线也互相平行；②两条直线被第三条直线所截，同旁内角互补；③两直线平行，内错角相等；④同一平面内，过一点有且只有一条直线与已知直线垂直；⑤从直线外一点到这条直线的垂线段，叫做这点到直线的距离.

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 如图，已知 $B D$ 为 $△ A B C$ 中 $∠ A B C$ 的平分线， $C D$ 为 $△ A B C$ 的外角 $∠ A C E$ 的平分线，与 $B D$ 交于点 $D$ ．若∠ABD=20°， $∠ A C D = 50 °$ ，则 $∠ A + ∠ D =$ （）

A、70° B、90° C、80° D、100°

查看试题解析
13. 在如图所示的四种沿AB进行折叠的方法中，不一定能判断纸带两条边a，b互相平行的是（　　）

A、如图1，展开后测得∠1=∠2 B、如图2，展开后测得∠1=∠2且∠3=∠4 C、如图3，测得∠1=∠2 D、在图④中，展开后测得∠1+∠2=180°

查看试题解析
14. 已知 ${(m + n)}^{2} = 11$ ， mn=2，则 ${(m - n)}^{2}$ 的值为（）

A、7 B、5 C、3 D、1

查看试题解析
15. 实数a，b，c在数轴上对应的点如图所示，则下列式子中正确的是（）

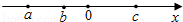A、a﹣c＞b﹣c B、a+c＜b+c C、ac＞bc D、 $\frac{a}{b} < \frac{c}{b}$

查看试题解析
16.
如图，∠B=∠C，∠A=∠D，下列结论：①AB∥CD；②AE∥DF；③AE⊥BC；④∠AMC=∠BND，其中正确的结论有（　　）

A、①②④ B、②③④ C、③④ D、①②③④

查看试题解析

二、填空题

17. 2019年我市地区生产总值逼近12000亿元，用科学记数法表示12000 是.

查看试题解析
18. 已知方程 $x - 2 y = 8$ ，用含有 $x$ 的式子表示 $y$ ，则．

查看试题解析
19. 如图，将分别含有 $30 °$ 、 $45 °$ 角的一副三角板重叠，使直角顶点重合，若两直角重叠形成的角为 $65 °$ ，则图中角 $α$ 的度数为.

查看试题解析
20.
一个大正方形和四个全等的小正方形按图①、②两种方式摆放，则图②的大正方形中未被小正方形覆盖部分的面积是（用a、b的代数式表示）．

查看试题解析

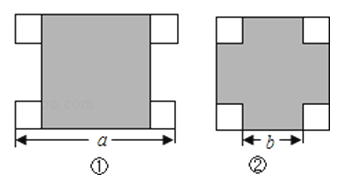
三、解答题

21.

(1)、计算： $- 2^{3} + \frac{1}{3} \times {(2005 + 3)}^{0} + {(- \frac{2}{3})}^{- 2}$

(2)、解方程组： ${\begin{array}{l} x - 2 y = 1 ① \\ 3 x - 5 y = 8 ② \end{array}$

(3)、解不等式 $\frac{1 + x}{2} - \frac{2 x + 1}{3} \leq 1$ ，并把解集在数轴上表示出来．

查看试题解析
22. 已知 $x^{2} - 4 x - 1 = 0$ ，求代数式 ${(2 x - 3)}^{2} - (x + y) (x - y) - y^{2}$ 的值。

查看试题解析
23. 完成下列推理过程：
如图，已知∠A＝∠EDF，∠C＝∠F，求证：BC∥EF
证明：∵∠A＝∠EDF（已知）
∴                  ▲                  ∥                  ▲                  （                  ▲                  ）
∴∠C＝                  ▲                  （                  ▲                  ）
又∵∠C＝∠F（已知）
∴                  ▲                  ＝∠F（等量代换）
∴                  ▲                  ∥                  ▲                  （                  ▲                  ）

查看试题解析
24. 发现任意五个连续整数的平方和是5的倍数．

(1)、验证（–1）²+0²+1²+2²+3²的结果是5的几倍？

(2)、设五个连续整数的中间一个为n，写出它们的平方和，并说明是5的倍数．

(3)、延伸任意三个连续整数的平方和被3除的余数是几呢？请写出理由．

查看试题解析
25. 某服装店用6000元购进A，B两种新式服装，按标价售出后可获得毛利润3800元（毛利润=售价−进价），这两种服装的进价，标价如表所示．
类型价格
A型
B型
进价（元/件）
60
100
标价（元/件）
100
160

(1)、求这两种服装各购进的件数；

(2)、如果A种服装按标价的8折出售，B种服装按标价的7折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元?

查看试题解析
26.

(1)、如图， $△ A B C$ 中，点D、E在边 $B C$ 上， $A D$ 平分 $∠ B A C$ ， $A E ⊥ B C$ ， $∠ B = 35 °$ ， $∠ C = 65 °$ ，求 $∠ D A E$ 的度数；

(2)、如图，若把（1）中的条件“ $A E ⊥ B C$ ”变成“F为 $D A$ 延长线上一点， $F E ⊥ B C$ ”，其它条件不变，求 $∠ D F E$ 的度数；

(3)、若把（1）中的条件“ $A E ⊥ B C$ ”变成“F为 $A D$ 延长线上一点， $F E ⊥ B C$ ”，其它条件不变，请画出相应的图形，并求出 $∠ D F E$ 的度数；

(4)、结合上述三个问题的解决过程，你能得到什么结论？

查看试题解析

类型价格	A型	B型
进价（元/件）	60	100
标价（元/件）	100	160