河北省沧州市沧县2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 在同一平面内,两条直线的位置关系可能是( )A、相交或垂直 B、垂直或平行 C、平行或相交 D、相交或垂直或平行
-
2. 下列选项中,平移左边三角形能与右边三角形重合的选项是( )A、
 B、
B、 C、
C、 D、
D、
-
3. 证明命题“若(a﹣1)2>1,则a>2”是假命题,下面所举反例正确的是( )A、a=2 B、a=1 C、a=0 D、a=﹣1
-
4. 下列命题是真命题的有( )
⑴相等的角是对顶角;(2)两条直线被第三条直线所截,同位角相等;(3)在同一平面内,过两点有且只有一条直线与已知直线垂直;(4)经过直线外一点,有且只有一条直线与已知直线平行;(5)一个角的余角一定大于这个角.
A、0个 B、1个 C、2个 D、3个 -
5. 下列四个图中,∠1=∠2一定成立的是( )A、
 B、
B、 C、
C、 D、
D、
-
6. 如图,∠B的同旁内角有( )
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个 -
7. 如图,田地A的旁边有一条小河l,要想把小河里的水引到田地A处,为了省时省力需要作AB⊥l,垂足为B,沿AB挖水沟,则水沟最短,理由是( )
 A、点到直线的距离 B、两点确定一条直线 C、垂线段最短 D、两点之间,线段最短
A、点到直线的距离 B、两点确定一条直线 C、垂线段最短 D、两点之间,线段最短 -
8. 如图,点E在AB的延长线上,下列条件中可以判断ABDC的是( )
 A、∠A=∠5 B、∠3=∠4 C、∠ABC+∠C=180° D、∠ADC=∠ABC
A、∠A=∠5 B、∠3=∠4 C、∠ABC+∠C=180° D、∠ADC=∠ABC -
9. 如图,把三角尺的直角顶点放在直尺的一边上,若∠2=58°,则∠1的度数为( )
 A、58° B、48° C、42° D、32°
A、58° B、48° C、42° D、32° -
10. 四根火柴棒摆成如图所示的象形“口”字,平移此象形字火柴棒后,变成的象形文字正确的是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
11. 如图,已知ABCD,∠ECA=120°,∠ECD=120°,∠A的度数是( )
 A、30° B、45° C、60° D、65°
A、30° B、45° C、60° D、65° -
12. 在如图所示的四种沿AB进行折叠的方法中,不一定能判断纸带两条边a,b互相平行的是( )
 A、如图1,展开后测得∠1=∠2 B、如图2,展开后测得∠1=∠2且∠3=∠4 C、如图3,测得∠1=∠2 D、在图④中,展开后测得∠1+∠2=180°
A、如图1,展开后测得∠1=∠2 B、如图2,展开后测得∠1=∠2且∠3=∠4 C、如图3,测得∠1=∠2 D、在图④中,展开后测得∠1+∠2=180° -
13. 如图,两个直角三角形重叠在一起,将ABC沿AB方向平移2cm得到DEF,CH=2cm,EF=4cm,下列结论:①BHEF;②AD=BE;③DH=CH;④∠C=∠BHD;⑤阴影部分的面积为6cm2 . 其中正确的是( )
 A、①②③④⑤ B、②③④⑤ C、①②③⑤ D、①②④⑤
A、①②③④⑤ B、②③④⑤ C、①②③⑤ D、①②④⑤ -
14. 某学员在驾校练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则两次拐弯的角度可能是( )A、第一次向左拐30°,第二次向右拐30° B、第一次向左拐45°,第二次向左拐45° C、第一次向左拐60°,第二次向右拐120° D、第一次向左拐53°,第二次向左拐127°
-
15. 如图,AB EF,∠D=90°,则 , , 的大小关系是( )
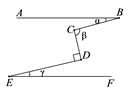 A、 B、 C、 D、
A、 B、 C、 D、 -
16. 为了亮化某景点,石家庄市在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转,B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动30°,B灯每秒转动10°,B灯先转动2秒,A灯才开始转动,当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是( )
 A、1或6秒 B、8.5秒 C、1或8.5秒 D、2或6秒
A、1或6秒 B、8.5秒 C、1或8.5秒 D、2或6秒
二、填空题
-
17. 如图,在三角形ABC中,∠C=90°,AC+BC=31,AB=25,则内部五个小直角三角形周长的和为 .

-
18. 如图,直线AB、CD相交于点O,射线OM平分∠AOC,∠MON=90°.若∠BOD=80°,则∠BON的度数为 .

-
19. 将一副三角板按如图放置,∠BAC=∠DAE=90°,∠B=45°,∠E=60°,则∠1=(填角),∠CAD+(填角)=180°.若ACDE,则∠2=°.

三、解答题
-
20. 如图,ABC的顶点都在方格纸的格点上,将ABC向左平移2格,再向上平移3格,其中每个格子的边长为1个单位长度.
 (1)、画出ABC的边AB上的高CD(过点C画出线段AB的垂线);(2)、请在图中画出平移后的 , 并求出此时的面积;(3)、若连接 , , 则这两条线段之间的关系是 .
(1)、画出ABC的边AB上的高CD(过点C画出线段AB的垂线);(2)、请在图中画出平移后的 , 并求出此时的面积;(3)、若连接 , , 则这两条线段之间的关系是 . -
21. 光线在不同的介质中传播的速度是不同的,因此当光线从水中射向空气时,要发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的.如图所示,恰有两束平行光线从水中射向空气,∠1=30°,∠2=130°.
 (1)、分别指出图中的两对同位角,一对内错角;(2)、求∠3,∠5,∠8的度数,并判断∠1和∠4是否互补.
(1)、分别指出图中的两对同位角,一对内错角;(2)、求∠3,∠5,∠8的度数,并判断∠1和∠4是否互补. -
22. 如图,直线AB、CD交于点O,OM⊥AB,垂足为O.
 (1)、若∠1=∠2.求∠NOD的度数;(2)、若∠AOD=4∠1,求∠AOC和∠MOD的度数.
(1)、若∠1=∠2.求∠NOD的度数;(2)、若∠AOD=4∠1,求∠AOC和∠MOD的度数. -
23. 如图,AB和CD相交于点O,E为线段AC上一点,过点E作EFAB交DB延长线于F,∠C=∠COA,∠D=∠BOD.
求证:∠A=∠F,下面是小明同学进行的说理,请你将小明同学的说理过程或说理根据补充完整.
证明:∵∠C=∠COA,∠D=∠BOD(已知),
且∠COA=∠BOD( ▲ ).
∴∠C= ▲ ( ▲ ).
∴ACDF( ▲ ).
∴∠A= ▲ ( ▲ ).
∵EFAB(已知),
∴∠F= ▲ ( ▲ ).
∴∠A=∠F( ▲ ).

-
24. 问题情境:如图,已知ABCD.∠1+∠2=180°.
 (1)、猜想论证:试猜想AD与CE的位置关系,并说明理由;(2)、拓展探究:若CE⊥AE于点E.∠2=145°,请自行给∠ABF或∠ABD一个合适的值,再求∠F的度数.
(1)、猜想论证:试猜想AD与CE的位置关系,并说明理由;(2)、拓展探究:若CE⊥AE于点E.∠2=145°,请自行给∠ABF或∠ABD一个合适的值,再求∠F的度数. -
25. 如图,有如下四个论断:① , ② , ③平分 , ④平分 .
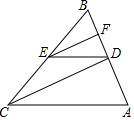 (1)、若选择四个论断中的三个作为条件,余下的一个论断作为结论,构成一个数学命题,其中正确的有哪些?不需说明理由.(2)、请你在上述正确的数学命题中选择一个进行说明理由.
(1)、若选择四个论断中的三个作为条件,余下的一个论断作为结论,构成一个数学命题,其中正确的有哪些?不需说明理由.(2)、请你在上述正确的数学命题中选择一个进行说明理由. -
26.(1)、引入:在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,如图是一个“美味”的模型—“猪蹄模型”.如图所示,ABCD,点E在直线AB与CD之间,连接AE、CE,求证:∠AEC=∠BAE+∠DCE.

嘉琪想到了下面的思路,请根据思路继续完成求证:
证明:如图,过点E作EFAB.
 (2)、思考:当点E在如图所示的位置时,其他条件不变,写出∠BAE,∠AEC,∠DCE三者之间的数量关系并说明理由.
(2)、思考:当点E在如图所示的位置时,其他条件不变,写出∠BAE,∠AEC,∠DCE三者之间的数量关系并说明理由. (3)、应用:如图,延长线段AE交直线CD于点M,已知∠BAE=132°,∠DCE=118°,求∠MEC的度数.
(3)、应用:如图,延长线段AE交直线CD于点M,已知∠BAE=132°,∠DCE=118°,求∠MEC的度数. (4)、提升:点E、F、G在直线AB与CD之间,连接AE、EF、FG和CG,其他条件不变,如图.若∠EFG=m°,直接写出∠BAE+∠AEF+∠FGC+∠DCG的总度数.
(4)、提升:点E、F、G在直线AB与CD之间,连接AE、EF、FG和CG,其他条件不变,如图.若∠EFG=m°,直接写出∠BAE+∠AEF+∠FGC+∠DCG的总度数.
