河北省保定市高碑店市2020-2021学年七年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. $a^{6}$ 可以写成（）

A、 $a^{7} \div a$ B、 $a^{2} \cdot a^{3}$ C、 ${(a^{2})}^{4}$ D、 $a^{3} + a^{3}$

查看试题解析
2. 在等式 $x^{4} \cdot$ □ $= x^{11}$ 中，“□”所表示的代数式为（）

A、 $x^{6}$ B、 $- x^{6}$ C、 ${(- x)}^{7}$ D、 $x^{7}$

查看试题解析
3. 如图，与 $∠ 4$ 是同位角的是（）

A、 $∠ 2$ B、 $∠ 3$ C、 $∠ 1$ D、 $∠ 5$

查看试题解析
4. 如图，OE⊥AB，直线CD经过点O，∠COA＝35°，则∠BOD的余角度数为（）

A、35° B、45° C、55° D、60°

查看试题解析
5. 把一副直角三角尺按如图方式摆放，点 $C$ 与点 $E$ 重合， $B C$ 边与 $E F$ 边都在直线 $l$ 上，若直线 $M N / / A C$ ，且 $M N$ 经过点 $D$ ，则 $∠ C D N =$ （）

A、 $30 °$ B、 $45 °$ C、 $65 °$ D、 $75 °$

查看试题解析
6. 在下列多项式的乘法中，不可以用乘法公式计算的是（）

A、 $(2 m + n) (2 n - m)$ B、 $(\frac{1}{2} m + 3) (- \frac{1}{2} m - 3)$ C、 $(5 m - 3 n) (5 m + 3 n)$ D、 $(- m + n) (m - n)$

查看试题解析
7. 用科学记数法将某小数表示为 $2 \times 1 0^{- 3}$ ，则这个小数为（）

A、 $- 0.02$ B、 $0.002$ C、 $0.02$ D、 $- 0.002$

查看试题解析
8. 将一副三角板按如图方式摆放，则下列结论不正确的是（）

A、 $∠ 1 = 135 °$ B、 $∠ 2 = 145 °$ C、 $∠ 1 = ∠ 2$ D、 $∠ 1 + ∠ 2 = 270 °$

查看试题解析
9. 某农场有耕地 $20$ 公顷，拖拉机需要 $100$ 小时耕完，则未耕地的面积 $Q$ （公顷）与拖拉机耕地的时间 $t$ （小时）间的关系式是（）

A、 $Q = 20 - 5 t$ B、 $Q = \frac{1}{5} t + 20$ C、 $Q = 20 - \frac{1}{5} t$ D、 $Q = \frac{1}{5} t$

查看试题解析
10. 计算 $202 1^{2} - 2019 \times 2023$ 的结果为（）

A、 $4$ B、 $3$ C、 $2$ D、 $1$

查看试题解析
11. 下面四个整式中，不能表示图中阴影部分面积的是（）

A、 $x (x + 3) + 3$ B、 $(x + 3) (x + 1) - x$ C、 $3 (x + 1) + x^{2}$ D、 $(x + 3) (2 x + 1)$

查看试题解析
12. 计算 $0.7 5^{2020} \times {(- \frac{4}{3})}^{2021}$ 的结果是（）

A、 $\frac{4}{3}$ B、 $- \frac{4}{3}$ C、 $0 ． 75$ D、 $- 0 ． 75$

查看试题解析
13. 如图，下列推理正确的是（）

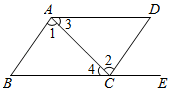A、∵AB∥CD，∴∠B＝∠DCE（两直线平行，同位角相等） B、∵∠1＝∠2，∴AD∥BC（内错角相等，两直线平行） C、∵AD∥BC，∴∠3＝∠4（内错角相等，两直线平行） D、∵∠B+∠BCD＝180°，∴AD∥BC（同旁内角互补，两直线平行）

查看试题解析
14. 在计算 $2 x + m$ 与 $x + 3$ 的乘积时，如果结果中只含有两项，则 $m$ 的值为（）

A、 $- 6$ B、 $0$ C、 $- 6$ 或 $0$ D、以上答案都错误

查看试题解析
15. 若 $x^{2} - 2 x - 3 = (x - a) (x + b)$ ，则 $a - b$ 的值为（）

A、 $3$ B、 $- 3$ C、 $2$ D、 $- 2$

查看试题解析
16. 在烧水时，水温达到 $100 ℃$ 就会沸腾，下表是某同学做“观察水的沸腾”实验时所记录的水的温度 $T (℃)$ 和烧水的时间 $t (m i n)$ 的数据：
$t (m i n)$
$0$
$2$
$4$
$6$
$8$
$10$
$12$
$14$
…
$T (℃)$
$30$
$44$
$58$
$72$
$86$
$100$
$100$
$100$
…
则下列说法不正确的是（）

A、烧水的时间 $t (m i n)$ 是自变量，水的温度 $T (℃)$ 是因变量 B、在水沸腾之前，每增加 $1$ 分钟，温度增加 $7 ℃$ C、烧水 $10$ 分钟后，水达到沸腾状态 D、温度 $T$ 与时间 $t$ 的关系式为 $T = 7 t + 30$

查看试题解析

二、填空题

17. 若 $x^{2} - 2 x + m - 1$ 是一个完全平方式，则m= ．

查看试题解析
18. $A$ ， $B$ 两块长方形板材的规格如图所示（ $m$ 为正整数），设板材 $A$ ， $B$ 面积分别为 $S_{1}$ ， $S_{2}$ ．小明和小刚对这两块板材的面积进行了讨论：小明说，估计它们的面积相等；小刚说，我们可以作差比较一下．则：

(1)、 $S_{1} - S_{2} =$ ．

(2)、 $S_{1}$ $S_{2}$ （填“＞”“＜”或“＝”）

查看试题解析
19. 图中的黑白方块是有规律地排列的设 $y$ 为第 $n$ 个图形中黑方块的个数．

(1)、第6个图形中，黑方块有个；

(2)、当 $n$ 为奇数时， $y$ 与 $n$ 的关系式为．

查看试题解析

三、解答题

20. 计算或化简：

(1)、 $| - 5 | - {(3 - π)}^{0} - {(\frac{1}{2})}^{- 3}$ ；

(2)、 ${(- 2 m^{2} n)}^{2} \div m n^{4} \cdot \frac{1}{2} n^{3}$ ；

(3)、 $(2 x + 3) (- x - 1) + 2 x (x - 3)$ ．

查看试题解析
21. 先化简，再求值： ${(x - y)}^{2} - (x + y) (x - y) - 3 y (y - 2 x)$ ，其中 $x = - \frac{1}{2}$ ， $y = - 2$ ．

查看试题解析
22. 如图，已知线段 $A C = 5$ ，射线 $C P$ 与 $A C$ 的夹角 $∠ A C P = 45 °$ ．

(1)、请用尺规作图法在 $C P$ 上求作一点 $B$ ，使 $∠ C A B = 45 °$ ．（保留作图痕迹，不写作法）

(2)、点 $A$ 到 $C P$ 的距离是线段的长度，其距离5．（填“大于”“小于”或“等于”）

查看试题解析
23. 如图，已知 $∠ 1 + ∠ 2 = 180 °$ ．

(1)、当 $∠ A G F$ 与 $∠ A B C$ 满足什么关系时， $B F / / D E$ ？并说明理由；

(2)、在（1）的条件下，若 $B F ⊥ A C$ ， $∠ 2 = 145 °$ ，求 $∠ A F G$ 的度数．

查看试题解析
24. 学完整式的乘法公式后，爱思考的小丽同学为了探究公式之间的联系，她把一个长为 $2 a$ ，宽为 $2 b$ 的长方形沿图1中虚线用剪刀平均分成四个小长方形，然后拼成一个大正方形（如图2）．请你根据小丽的操作回答下列问题：

(1)、图1中每个小长方形的长和宽分别为，图2中大正方形的边长为，中间小正方形（阴影部分）的边长为（均用含 $a$ ， $b$ 的式子表示）；

(2)、小丽发现可以用两种方法求图2中小正方形（阴影部分）的面积，请你帮她写出来（直接用含 $a$ ， $b$ 的式子表示，不必化简）：
方法1：，方法2：；

(3)、根据（2）中的结论，探究 ${(a + b)}^{2}$ ， ${(a - b)}^{2}$ ， $a b$ 间的等量关系；

(4)、根据（3）中的等量关系，解决如下问题：知 $a$ ， $b$ 满足 $a + b = 5$ ， $a - b = 1$ ，请求出 $a b$ 的值．

查看试题解析
25. 周末上午8：00，小颖陪妈妈骑自行车去塞外天路踏青，沿途观赏了一个种植园，中午时分到达目的地塞外天路的一个农家院就餐，随后返回家中，如图是她们离农家院的距离 $s (k m)$ 与时间 $t$ （时）之间的关系．请根据图象回答下列问题：

(1)、农家院离家多远？并说出 $A B$ 和 $C D$ 段的实际意义（什么时间段内干了什么事情）；

(2)、求去时她们骑自行车的平均速度（停车观赏种植园除外）；

(3)、她们何时与家相距 $10 k m$ ？

查看试题解析
26. 已知 $A B / / C D$ ， $∠ M P N = 60 °$ ．

(1)、如图1，若点 $P$ 落在 $C D$ 上，且 $P N ⊥ C D$ ，则 $∠ A M P$ 的度数为；

(2)、如图2，点 $P$ 落在 $A B$ 与 $C D$ 之间，且两边分别与 $A B$ ， $C D$ 相交．
①若 $∠ B N P = 20 °$ ，则 $∠ D M P$ 的度数为 ▲ ，你能发现 $∠ B N P$ 与 $∠ D M P$ 之间的关系吗？直接写出结果；
②若改变 $∠ B N P$ 的度数，①中的结论是否还成立？如果成立，请推理说明；如果不成立，请说明理由．
③如图3，作 $∠ B N P$ 与 $∠ D M P$ 的平分线交于点 $P_{1}$ ，再作 $∠ B N P_{1}$ 与 $∠ D M P_{1}$ 的平分线交于点 $P_{2}$ ， …，以此类推，作 $2021$ 次，请直接写出 $∠ P_{2021}$ 的度数．

查看试题解析

$t (m i n)$	$0$	$2$	$4$	$6$	$8$	$10$	$12$	$14$	…
$T (℃)$	$30$	$44$	$58$	$72$	$86$	$100$	$100$	$100$	…