河北省保定市2020-2021学年七年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 计算:m6•m2的结果为( )A、m12 B、m8 C、m4 D、m32. 三角形的重心是( )A、三角形三条边上中线的交点 B、三角形三条边上高线的交点 C、三角形三条边垂直平分线的交点 D、三角形三条内角平行线的交点3. 如图,小华同学的家在点处,他想尽快到达公路边去接从外地回来的外婆,他选择路线时所用到的数学知识是( )
 A、两点确定一条直线 B、两点之间直线最短 C、两点之间线段最短 D、垂线段最短4. 将9.52变形正确的是( )
A、两点确定一条直线 B、两点之间直线最短 C、两点之间线段最短 D、垂线段最短4. 将9.52变形正确的是( )
A、9.52=92+0.52 B、9.52=(10+0.5)(10﹣0.5) C、9.52=102﹣2×10×0.5+0.52 D、9.52=92+9×0.5+0.525. 把写成( , 为整数)的形式,则为( )A、5 B、 C、2 D、6. 等腰三角形的周长为13cm,其中一边长为3cm,则该等腰三角形的底边长为( )A、7cm B、3cm C、7cm或3cm D、5cm7. 下列符合题意说法的个数是( )①同位角相等;②等角的补角相等;③两直线平行,同旁内角相等;④在同一平面内,过一点有且只有一条直线与已知直线垂直.
A、1 B、2 C、3 D、48. 下列四个图形中,线段BE是△ABC的高的是( )A、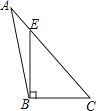 B、
B、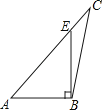 C、
C、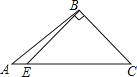 D、
D、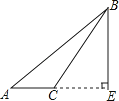 9. 如图,下列判断中不正确的是( )
9. 如图,下列判断中不正确的是( ) A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以10. 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( )
A、因为 , 所以 B、因为 , 所以 C、因为 , 所以 D、因为 , 所以10. 如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC.将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线.此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则说明这两个三角形全等的依据是( ) A、SAS B、ASA C、AAS D、SSS11. 有足够多的如图所示的正方形和长方形卡片,如果要拼成一个长为 , 宽为的长方形,则需要、、类卡片的张数分别为( )
A、SAS B、ASA C、AAS D、SSS11. 有足够多的如图所示的正方形和长方形卡片,如果要拼成一个长为 , 宽为的长方形,则需要、、类卡片的张数分别为( ) A、1、2、3 B、2、1、3 C、1、3、2 D、2、3、112. 若要使4x2+mx+成为一个两数差的完全平方式,则m的值应为( )A、± B、- C、± D、-13. 下列各式中,计算结果正确的是( )A、 B、 C、 D、14. 如图,三条直线相交于点 . 若 , , 则的补角等于( )
A、1、2、3 B、2、1、3 C、1、3、2 D、2、3、112. 若要使4x2+mx+成为一个两数差的完全平方式,则m的值应为( )A、± B、- C、± D、-13. 下列各式中,计算结果正确的是( )A、 B、 C、 D、14. 如图,三条直线相交于点 . 若 , , 则的补角等于( ) A、150° B、34° C、56° D、146°15. 如图,小辉从家(点O)出发,沿着等腰三角形AOB的边OA-AB-BO的路径去匀速散步,其中OA=OB.设小辉距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )
A、150° B、34° C、56° D、146°15. 如图,小辉从家(点O)出发,沿着等腰三角形AOB的边OA-AB-BO的路径去匀速散步,其中OA=OB.设小辉距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、 16. 如图,一艘轮船在处看见巡逻艇在其北偏东的方向上,此时一艘客船在处看见巡逻艇在其北偏东的方向上,则此时从巡逻艇上看这两艘船的视角( )
16. 如图,一艘轮船在处看见巡逻艇在其北偏东的方向上,此时一艘客船在处看见巡逻艇在其北偏东的方向上,则此时从巡逻艇上看这两艘船的视角( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 若 , , 则 .18. 正方形边长3,若边长增加x,则面积增加y,y与x的函数关系式为 .19. 如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数 .

三、解答题
-
20. 计算:(1)、(2)、(3)、(4)、(5)、先化简,再求值 , 其中 , .21. 如图,点、分别在、上,小华想知道和是否互补,但是他没有带量角器,只带了一副三角板,于是他想了这样一个办法:首先连接 , 再找出的中点 , 连接并延长和直线相交于点 , 经过测量他发现 , 因他得出结论:和互补,而且他还发现小华是这样想的:

∵和相交于
∴;( ▲ )
又∵是的中点,
∴ , ( ▲ )
又∵
∴≌ . ( ▲ )
∴ . ( ▲ )
. ( ▲ )
∴( ▲ )
∴( ▲ )
请把理由填在括号里
22. 乘法公式的探究及应用. (1)、如图 1,可以求出阴影部分的面积是(写成两数平方差的形式);(2)、如图 2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 , 长是 , 面积是(写成多项式乘法的形式)(3)、比较图 1,图 2 的阴影部分面积,可以得到乘法公式(用式子表达)(4)、应用所得的公式计算:(1﹣ )(1﹣ )(1﹣ )…(1﹣ )(1﹣ )23. 巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)、如图 1,可以求出阴影部分的面积是(写成两数平方差的形式);(2)、如图 2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 , 长是 , 面积是(写成多项式乘法的形式)(3)、比较图 1,图 2 的阴影部分面积,可以得到乘法公式(用式子表达)(4)、应用所得的公式计算:(1﹣ )(1﹣ )(1﹣ )…(1﹣ )(1﹣ )23. 巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题: (1)、在上述变化过程中,自变量是 , 因变量是;(2)、朱老师的速度为米/秒,小明的速度为米/秒;(3)、当小明第一次追上朱老师时,求小明距起点的距离是多少米?24. 两个边长分别为a和b的正方形如图放置(图①),其未叠合部分(阴影)面积为;若再在图①中大正方形的右下角摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为 .
(1)、在上述变化过程中,自变量是 , 因变量是;(2)、朱老师的速度为米/秒,小明的速度为米/秒;(3)、当小明第一次追上朱老师时,求小明距起点的距离是多少米?24. 两个边长分别为a和b的正方形如图放置(图①),其未叠合部分(阴影)面积为;若再在图①中大正方形的右下角摆放一个边长为b的小正方形(如图②),两个小正方形叠合部分(阴影)面积为 . (1)、用含a、b的代数式分别表示、;(2)、若 , , 求的值;(3)、用a、b的代数式表示;并当时,求出图③中阴影部分的面积 .25. 问题背景
(1)、用含a、b的代数式分别表示、;(2)、若 , , 求的值;(3)、用a、b的代数式表示;并当时,求出图③中阴影部分的面积 .25. 问题背景如图1,已知 , 写出、与之间的数量关系,并说明理由.


 (1)、知识迁移
(1)、知识迁移如图2, , , 则 .
(2)、方法应用如图3,一条公路修到湖边时,需拐弯绕湖而过,在 , , 三处经过三次拐弯此时道路恰好和第一次拐弯之前的道路平行(即),若 , , 则的度数是 .