山东省淄博市高青县2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 已知三点M、N、G,画直线MN、画射线MG、连结NG,按照上述语句画图正确的是( )A、
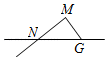 B、
B、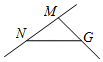 C、
C、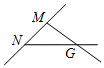 D、
D、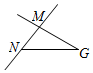 2. 等于( )A、-8 B、8 C、0.125 D、-0.1253. 若 , , 则等于( )A、 B、6 C、21 D、204. 如图,C是线段的中点,D为线段上一点,下列等式:(1);(2);(3) , 其中正确的有( )
2. 等于( )A、-8 B、8 C、0.125 D、-0.1253. 若 , , 则等于( )A、 B、6 C、21 D、204. 如图,C是线段的中点,D为线段上一点,下列等式:(1);(2);(3) , 其中正确的有( )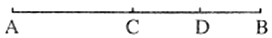 A、0个 B、1个 C、2个 D、3个5. 已知 ,则 的值为( )A、5 B、10 C、32 D、646. 已知 , 则的大小关系为( )A、 B、 C、 D、7. 关于比较38°15'和38.15°,下列说法正确的是( )A、38°15'>38.15° B、38°15'<38.15° C、38°15'=38.15° D、无法比较8. 若展开后不含x的一次项,则p与q的关系是( )A、 B、 C、 D、9. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,再将剩下的阴影部分剪开,拼成下边的长方形.根据图形的变化过程可以验证下列哪一个等式成立( ).
A、0个 B、1个 C、2个 D、3个5. 已知 ,则 的值为( )A、5 B、10 C、32 D、646. 已知 , 则的大小关系为( )A、 B、 C、 D、7. 关于比较38°15'和38.15°,下列说法正确的是( )A、38°15'>38.15° B、38°15'<38.15° C、38°15'=38.15° D、无法比较8. 若展开后不含x的一次项,则p与q的关系是( )A、 B、 C、 D、9. 如图,从边长为a的大正方形中剪掉一个边长为b的小正方形,再将剩下的阴影部分剪开,拼成下边的长方形.根据图形的变化过程可以验证下列哪一个等式成立( ). A、 B、 C、 D、10. 已知∠AOB=70°,以O端点作射线OC,使∠AOC=28°,则∠BOC的度数为( )A、42° B、98° C、42°或98° D、82°11. 已知x=3y+5,且x2﹣7xy+9y2=24,则x2y﹣3xy2的值为( )A、0 B、1 C、5 D、1212. 4张长为a、宽为 的长方形纸片,按如图的方式拼成一个边长为 的正方形,图中空白部分的面积为 ,阴影部分的面积为 .若 ,则a、b满足( )
A、 B、 C、 D、10. 已知∠AOB=70°,以O端点作射线OC,使∠AOC=28°,则∠BOC的度数为( )A、42° B、98° C、42°或98° D、82°11. 已知x=3y+5,且x2﹣7xy+9y2=24,则x2y﹣3xy2的值为( )A、0 B、1 C、5 D、1212. 4张长为a、宽为 的长方形纸片,按如图的方式拼成一个边长为 的正方形,图中空白部分的面积为 ,阴影部分的面积为 .若 ,则a、b满足( )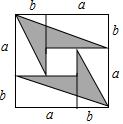 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
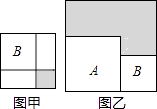
13. 计算:2020×2018﹣20192= .14. 一个 n 边形过一个顶点有 5 条对角线,则 n= .15. (3a5−2a4)÷(−a)3= .16. 若x﹣y=a , xy=a+3,且x2+y2=5,则a的值为 .17. 有两个正方形A,B,现将B放在A的内部得图甲,将A,B并列放置后构造新的正方形得图乙.若图甲和图乙中阴影部分的面积分别为1和12,则正方形A,B的面积之和为 .
三、解答题
-
18. 计算:(1)、(-3x2y)3•(6xy3)÷(9x3y4)(2)、(-)-2-8×(-2)-2+(-1)2019-(0.5)-119. 如图,点C ,E是线段AB上两点,点D为线段AB的中点,AB=6,CD=1.
 (1)、求 BC 的长;(2)、若 AE: EC 1:3 ,求 EC 的长.20. 先化简,再求值[(2x+y)(2x-y)-(2x-3y)2]÷2y,其中 x=2,y=121.(1)、已知am=2,an=3,求am+n的值;(2)、已知3x+1=81,求x.22. 甲、乙两个长方形的边长如图所示(m 为正整数),其面积分别为 S1 , S2 .
(1)、求 BC 的长;(2)、若 AE: EC 1:3 ,求 EC 的长.20. 先化简,再求值[(2x+y)(2x-y)-(2x-3y)2]÷2y,其中 x=2,y=121.(1)、已知am=2,an=3,求am+n的值;(2)、已知3x+1=81,求x.22. 甲、乙两个长方形的边长如图所示(m 为正整数),其面积分别为 S1 , S2 .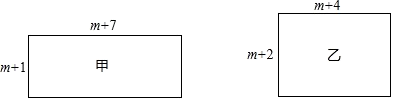 (1)、填空:S1-S2=(用含 m 的代数式表示);(2)、若一个正方形的周长等于甲、乙两个长方形的周长之和.
(1)、填空:S1-S2=(用含 m 的代数式表示);(2)、若一个正方形的周长等于甲、乙两个长方形的周长之和.①设该正方形的边长为 x,求 x 的值(用含 m 的代数式表示);
②设该正方形的面积为 S3 , 试探究:S3 与 2(S1+S2)的差是否是常数?若是常数,求出这个常数,若不是常数,请说明理由,
23. 如图(1), 点 为直线 上一点,过点 作射线 , 将一直角的直角顶点放在点 处,即 反向延长射线 ,得到射线 .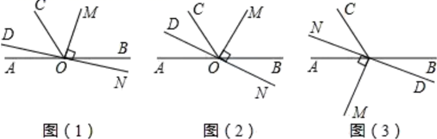 (1)、当 的位置如图(1)所示时,使 ,若 ,求 的度数.(2)、当 的位置如图(2)所示时,使一边 在 的内部,且恰好平分 ,
(1)、当 的位置如图(1)所示时,使 ,若 ,求 的度数.(2)、当 的位置如图(2)所示时,使一边 在 的内部,且恰好平分 ,问:射线 的反向延长线 是否平分 请说明理由:注意:不能用问题 中的条件
(3)、当 的位置如图 所示时,射线 在 的内部,若 .试探究 与 之间的数量关系,不需要证明,直接写出结论.24. 完全平方公式是同学们熟悉的公式,小玲同学在学习过完全平方公式后,通过类比学习得到(a+b)n(n 为非负整数)的计算结果,如果将(a+b)n(n 为非负整数)的每一项按字母 a 的次数由大到小排列,就可以得到下面的等式:(a+b)0=1,它只有一项,系数为 1;
(a+b)1=a+b,它有两项,系数分别为 1、1;
(a+b)2=a2+2ab+b2 , 它有三项,系数分别为 1、2、1;
(a+b)3=a3+3a2b+3ab2+b3 它有四项,系数分别为 1、3、3、1;
如果将上述每个式子的各项系数排成如图的表格,我们可以发现一些规律,聪明的你一定也发现了,请你根据规律解答下列问题:
(1)、尝试写出(a+b)4 的结果,并验证;(2)、请直接写出(a+b)5 共有项,各项系数的和等于;(3)、(a+b)n(n 为非负整数)共有项,各项系数的和等于;(a-b)n(n 为正整数)各项系数的和等于 .