山东省枣庄市市中区2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 下面给出的6个式子:①;②;③:④:⑤;⑥;其中不等式有( )A、2个 B、3个 C、4个 D、5个2. 如图,把线段AB经过平移得到线段CD,其中A,B的对应点分别为C,D.已知A(﹣1,0),B(﹣2,3),C(2,1),则点D的坐标为( )
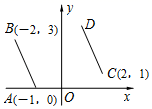 A、.(1,4) B、.(1,3) C、.(2,4) D、.(2,3)3. 已知等边三角形的边长为3,P为等边三角形内任意一点,则点P到三边的距离之和为( )A、 B、 C、 D、不能确定4.
A、.(1,4) B、.(1,3) C、.(2,4) D、.(2,3)3. 已知等边三角形的边长为3,P为等边三角形内任意一点,则点P到三边的距离之和为( )A、 B、 C、 D、不能确定4.在方格纸中,选择标有序号①②③④中的一个小正方形涂黑,与图中阴影部分构成中心对称图形.该小正方形的序号是( )
 A、① B、② C、③ D、④5. 如图, , , , 若 , 则为( )
A、① B、② C、③ D、④5. 如图, , , , 若 , 则为( )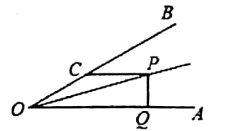 A、1 B、2 C、3 D、46. 如图,在方格纸上建立的平面直角坐标系中,将绕点O按顺时针方向旋转90°,得到 , 则点的坐标为( ).
A、1 B、2 C、3 D、46. 如图,在方格纸上建立的平面直角坐标系中,将绕点O按顺时针方向旋转90°,得到 , 则点的坐标为( ).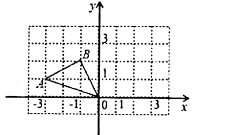 A、 B、 C、 D、7. 小明和爸爸、妈妈三人玩跷跷板.三人的体重一共为150千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端.这时爸爸那端仍然着地,那么小明的体重应小于( )A、49千克 B、50千克 C、24千克 D、25千克8. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
A、 B、 C、 D、7. 小明和爸爸、妈妈三人玩跷跷板.三人的体重一共为150千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端.这时爸爸那端仍然着地,那么小明的体重应小于( )A、49千克 B、50千克 C、24千克 D、25千克8. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB,AC于点M和N,再分别以M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
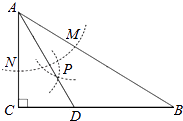 A、1 B、2 C、3 D、49. 如图,直线 经过点 ,则不等式 的解集为( )
A、1 B、2 C、3 D、49. 如图,直线 经过点 ,则不等式 的解集为( )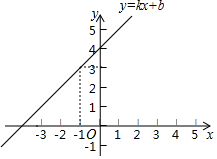 A、 B、 C、 D、10. 如图,P是正三角形内的一点,且 , , . 若将绕点A逆时针旋转后,得到 , 则等于( ).
A、 B、 C、 D、10. 如图,P是正三角形内的一点,且 , , . 若将绕点A逆时针旋转后,得到 , 则等于( ).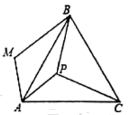 A、120° B、135° C、150° D、160°11. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )
A、120° B、135° C、150° D、160°11. 如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是( )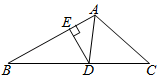 A、3 B、4 C、5 D、612. 若关于x的不等式组有且只有三个整数解,则实数a的取值范围是( ).A、 B、 C、 D、
A、3 B、4 C、5 D、612. 若关于x的不等式组有且只有三个整数解,则实数a的取值范围是( ).A、 B、 C、 D、二、填空题
-
13. 为了迎接“母亲节”的到来,枣庄市购物中心超市准备开展打折促销活动,现在有某件商品进价200元,标价320元出售,商场规定打折销售后利润率不能少于20%,那么这种商品最多打折.14. 随着人们生活水平的不断提高,汽车逐步进入到千家万户,小红的爸爸想在本镇的三条相互交叉的公路(如图所示),建一个加油站,要求它到三条公路的距离相等,这样可供选择的地址有处.
 15. 如果点P在第二象限,则关于x的不等式的解集是 .16. 如图,在△ABC中,∠B=90°,∠A=60°,BC=5,将△ABC沿直角边BC所在的直线向右平移2个单位长度,到达△DEF,AC与DE交于点G,则EG的长为 .
15. 如果点P在第二象限,则关于x的不等式的解集是 .16. 如图,在△ABC中,∠B=90°,∠A=60°,BC=5,将△ABC沿直角边BC所在的直线向右平移2个单位长度,到达△DEF,AC与DE交于点G,则EG的长为 .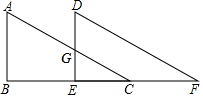 17. 若不等式组的解集为-1<x<1,那么(a-3)(b+3)的值等于 .18. 在平面直角坐标系中,的位置如图所示,将绕点O顺时针旋转90°得;再将绕点O顺时针旋转90°得;再将绕点O顺时针旋转90°得;……依此类推,第2021次旋转得到 , 则顶点A的对应点的坐标是 .
17. 若不等式组的解集为-1<x<1,那么(a-3)(b+3)的值等于 .18. 在平面直角坐标系中,的位置如图所示,将绕点O顺时针旋转90°得;再将绕点O顺时针旋转90°得;再将绕点O顺时针旋转90°得;……依此类推,第2021次旋转得到 , 则顶点A的对应点的坐标是 .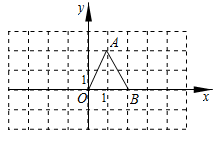
三、解答题
-
19. 对任意实数x、y,定义新运算 , 若 , 求x的取值范围并把它的解集在数轴上表示出来.20. 解不等式组: , 把它的解集在数轴上表示出来,并写出它的所有整数解.21. 如图所示∠A=∠D=90°,AB=DC,点E,F在BC上且BE=CF.
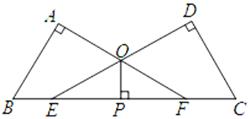 (1)、求证:AF=DE.(2)、若PO⊥EF,求证:OP平分∠EOF.22. 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).
(1)、求证:AF=DE.(2)、若PO⊥EF,求证:OP平分∠EOF.22. 如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(-2,2),B(0,5),C(0,2).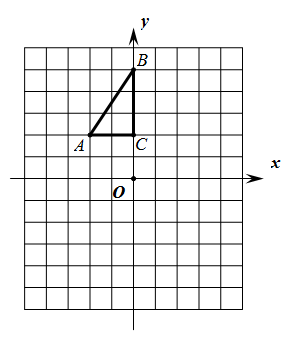
⑴将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
⑵平移△ABC,使点A的对应点A2坐标为(-2,-6),请画出平移后对应的△A2B2C2的图形.
⑶若将△A1B1C绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标.
23. 为了提倡低碳经济,某公司为了更好得节约能源,决定购买节省能源的10台新机器.现有甲、乙两种型号的设备供选择,其中每台的价格、工作量如下表:甲型
乙型
价格(万元/台)
12
10
产量(吨/月)
240
180
(1)、经预算:该公司购买的节能设备的资金不超过110万元,请列式解答有几种购买方案可供选择;(2)、在(1)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你设计一种最省钱的购买方案.24. 如图,在直角三角形中, , , , 点P从A开始沿边向点B以的速度移动,点Q从点B开始沿边向点C以的速度移动.P,Q分别从A,B同时出发,当一个动点到达终点则另一动点也随之停止运动.设运动时间为 , 则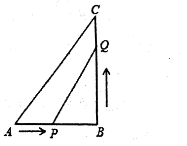 (1)、求t为何值时,为等腰三角形?(2)、是否存在某一时刻t,使点Q在线段的垂直平分线上?
(1)、求t为何值时,为等腰三角形?(2)、是否存在某一时刻t,使点Q在线段的垂直平分线上?