山东省烟台市招远市2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{\frac{1}{3}}$ 、 $\sqrt{12}$ 、 $\sqrt{30}$ 、 $\sqrt{5 x^{2}}$ 、 $\sqrt{x^{2} + y^{2}}$ 中，最简二次根式有（）个．

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 将方程x²+8x+9＝0配方后，原方程可变形为（）

A、(x+4)²＝7 B、(x+4)²＝25 C、(x+4)²＝﹣9 D、(x+8)²＝7

查看试题解析
3. 如图，下列条件不能判定四边形ABCD是矩形的是（　　）

A、∠DAB＝∠ABC＝∠BCD＝90° B、AB∥CD，AB＝CD，AB⊥AD C、AO＝BO，CO＝DO D、AO＝BO＝CO＝DO

查看试题解析
4. 若 $\sqrt{\frac{x + 1}{2 - x}} = \frac{\sqrt{x + 1}}{\sqrt{2 - x}}$ 成立，则x的值可以是（）

A、-2 B、0 C、2 D、3

查看试题解析
5. 已知m是方程x²﹣3x﹣2＝0的根，则代数式1＋6m﹣2m²的值为（）

A、5 B、－5 C、3 D、－3

查看试题解析
6. 如图，是一张平行四边形纸片ABCD，要求利用所学知识将它变成一个菱形，甲、乙两位同学的作法分别如下：

对于甲、乙两人的作法，可判断（）

A、甲正确，乙错误 B、甲错误，乙正确 C、甲、乙均正确 D、甲、乙均错误

查看试题解析
7. 计算 $4 \sqrt{\frac{1}{2}} - 6 \sqrt{\frac{1}{3}} + \sqrt{12}$ 的结果是（）

A、3 $\sqrt{2} - 2 \sqrt{3}$ B、5－ $\sqrt{2}$ C、5－ $\sqrt{3}$ D、2 $\sqrt{2}$

查看试题解析
8. 在▱ABCD中，E、F分别是AB、CD的中点，连接AF、CE．连接AC，当CA＝CB时，判断四边形AECF是（）

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
9. 已知实数a在数轴上的位置如图所示，则化简 $| a - 1 | + \sqrt{a^{2}}$ 的结果是（）

A、-1 B、1 C、1-2a D、2a-1

查看试题解析
10. 如图：将一个长方形纸片ABCD，沿着BE折叠，使C、D点分别落在点C₁ ， D₁处．若∠C₁BA＝56°，则∠ABE的度数为（　　）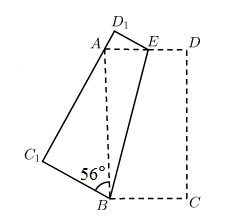

A、15° B、16° C、17° D、20°

查看试题解析
11. 若关于x的方程x²－4x＋k＝0的一个根为2－ $\sqrt{3}$ ，则k的值为（　　）

A、1 B、－1 C、2 D、－2

查看试题解析
12. 如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD上，下列结论：①CE＝CF；②∠AEB＝75°；③BE＋DF＝EF；④S_正方形ABCD＝2＋ $\sqrt{3}$ ，其中正确的序号是（）

A、①②③ B、②③④ C、①③④ D、①②④

查看试题解析

二、填空题

13. 若最简二次根式 $\sqrt{a + 3}$ 与 $\sqrt{8}$ 能合并成一项，则a＝．

查看试题解析
14. 关于x的方程 $(a - 5) x^{2} - 4 x - 1 = 0$ 有实数根，则a的取值范围是．

查看试题解析
15. 如图，在菱形ABCD中，∠B＝40°，点E在CD上，AE＝AC ，则∠BAE＝°．

查看试题解析
16. 化简 $(\sqrt{3} - 2)^{2021} \cdot (\sqrt{3} + 2)^{2020}$ 的结果为．

查看试题解析
17. 如图，小明同学将边长为5cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起，其中直角三角板的直角顶点落在点A处，两条直角边分别与CD交于点F，与CB延长线交于点E，则四边形AECF的面积是．

查看试题解析
18. 如图，在Rt△ABC中，AC＝3，BC＝4，D为斜边AB上一动点，DE⊥BC，DF⊥AC，垂足分别为E、F．则线段EF的最小值为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{18} - \sqrt{50} + 3 \sqrt{\frac{1}{2}}$

(2)、 $(\sqrt{5} + 1) (3 - \sqrt{5}) - \sqrt{20}$

查看试题解析
20. 按要求解下列方程：

(1)、x²﹣4x﹣1＝0（配方法）；

(2)、5x²﹣4x﹣1＝0（公式法）．

查看试题解析
21. 关于 $x$ 的一元二次方程 $x^{2} - 3 x + k = 0$ 有实数根．

(1)、求 $k$ 的取值范围；

(2)、如果 $k$ 是符合条件的最大整数，且一元二次方程 $(m - 1) x^{2} + x + m - 3 = 0$ 与方程 $x^{2} - 3 x + k = 0$ 有一个相同的根，求此时 $m$ 的值．

查看试题解析
22. 已知：如图，在菱形ABCD中， BE⊥AD于点E ，延长AD至F ，使DF=AE ，连接CF ．

(1)、判断四边形EBCF的形状，并证明；

(2)、若AF=9，CF=3，求CD的长．

查看试题解析
23. 小明在解决问题：已知a＝ $\frac{1}{2 + \sqrt{3}}$ ，求2a²﹣8a＋1的值时，他是这样分析与解的：
∵a＝ $\frac{1}{2 + \sqrt{3}}$ ＝ $\frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})}$ ＝2﹣ $\sqrt{3}$ ，
∴a﹣2＝﹣ $\sqrt{3}$ ，
∴（a﹣2）²＝3，a²﹣4a＋4＝3，
∴a²﹣4a＝﹣1，
∴2a²﹣8a＋1＝2（a²﹣4a）＋1＝2×（﹣1）＋1＝﹣1．
请你根据小明的分析过程，解决如下问题：

(1)、化简 $\frac{2}{3 - \sqrt{7}}$

(2)、化简 $\frac{1}{\sqrt{2} + 1}$ ＋ $\frac{1}{\sqrt{3} + \sqrt{2}}$ ＋ $\frac{1}{\sqrt{4} + \sqrt{3}}$ ＋…＋ $\frac{1}{\sqrt{100} + \sqrt{99}}$ ；

(3)、若a＝ $\frac{1}{\sqrt{2} - 1}$ ，求4a²﹣8a＋1的值．

查看试题解析
24. 如图1，在矩形纸片ABCD中，AB＝5cm，AD＝13cm，折叠纸片使C点落在边AD上的E处，折痕为MN，过点E作EF∥CD交MN于F，连接CF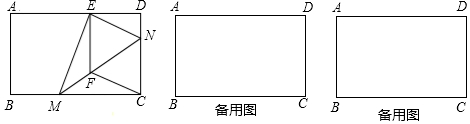

(1)、求证：四边形CFEN为菱形；

(2)、当点E在AD边上移动时，折痕的端点M、N也随之移动，若限定M、N分别在边BC、CD上移动，求出点E在边AD上移动的最大距离．

查看试题解析
25. 在菱形ABCD中，∠ABC＝60°，点P是射线BD上一动点，以AP为边向右侧作等边△APE，点E的位置随着点P的位置变化而变化．

(1)、如图1，点E在菱形ABCD内部或边上时，连接CE，BP与CE的数量关系， CE与AD的位置关系．

(2)、当点E在菱形ABCD外部时，（1）中的结论是否还成立？若成立，请予以证明；若不成立，请说明理由（选择图2，图3中的一种情况予以证明或说明）．

查看试题解析