山东省烟台市莱阳市2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，不是一元二次方程的是（）

A、 $x^{2} = - 3$ B、 $4 x^{2} + 2 x = 0$ C、 $3 x^{2} - 2 x + 1 = 0$ D、 $x^{2} + 6 x = (x + 2) (x - 2)$

查看试题解析
2. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{18}$ B、 $\sqrt{\frac{8}{5}}$ C、 $\sqrt{a^{2} + 1}$ D、 $\sqrt{x^{3} y}$

查看试题解析
3. 下列方程没有实数解的是（）

A、 $- x^{2} = 0$ B、 $1 + x^{2} = 0$ C、 $x^{2} + x - 1 = 0$ D、 $x^{2} - 2 x + 1 = 0$

查看试题解析
4. 在下列各组根式中，是同类二次根式的是（）．

A、 $\sqrt{2}$ 和 $\sqrt{12}$ B、 $\sqrt{2}$ 和 $\sqrt{\frac{1}{8}}$ C、 $\sqrt{a^{2} b}$ 和 $\sqrt{a b^{2}}$ D、 $\sqrt{a + 1}$ 和 $\sqrt{a - 1}$

查看试题解析
5. 如图，在正方形 $A B C D$ 中， $D E$ 是 $∠ B D C$ 的平分线，若正方形的边长是1，则 $C E$ 的长是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2} - 1$ C、 $\sqrt{2} - 1$ D、 $2 \sqrt{2} - 1$

查看试题解析
6. 用配方法解方程 $x^{2} - 2 x - 3 = 0$ ，下列变形正确的是（）

A、(x-2) ²=4 B、(x-1) ²=3 C、(x-1) ²=4 D、(x+1) ²=4

查看试题解析
7. 使 $\frac{x - 2}{\sqrt{x + 1}}$ 有意义的x的取值范围是（）

A、 $x > - 1$ 且 $x \neq 2$ B、 $x \geq - 1$ C、 $x < - 1$ D、 $x > - 1$

查看试题解析
8. 已知 $a \neq 0$ 且 $a < b$ ，化简二次根式 $\sqrt{- a^{3} b}$ 的正确结果是（）

A、 $a \sqrt{a b}$ B、 $- a \sqrt{a b}$ C、 $a \sqrt{- a b}$ D、 $- a \sqrt{- a b}$

查看试题解析
9. 如图，在长为 $62$ 米、宽为 $42$ 米的矩形草地上修同样宽的路，余下部分种植草坪，要使草坪的面积为 $2400$ 平方米，设道路的宽为x米．则可列方程为（）

A、 $(62 - x) (42 - x) = 2400$ B、 $(62 - x) (42 - x) + x^{2} = 2400$ C、 $62 \times 42 - 62 x - 42 x = 2400$ D、 $62 x + 42 x = 2400$

查看试题解析
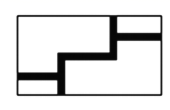10. 如图，在矩形ABCD中，边AB的长为3，点E，F分别在AD，BC上，连接BE，DF，EF，BD．若四边形BEDF是菱形，且EF=AE+FC，则边BC的长为（）

A、 $\sqrt{3}$ B、2 $\sqrt{3}$ C、3 $\sqrt{3}$ D、6 $\sqrt{3}$

查看试题解析
11. 如图，菱形ABCD的边长为4，过点A、C作对角线AC的垂线，分别交CB和AD的延长线于点E、F，AE=3，则四边形AECF的周长为（）．

A、22 B、18 C、14 D、11

查看试题解析
12. 如图，将矩形 $A B C D$ 沿 $E F$ 折叠，使点D落在点B处，点C落在点 $C^{'}$ 处，P为折痕 $E F$ 上的任意一点，过点P作 $P G ⊥ B E$ ， $P H ⊥ B C$ ，垂足分别为G，H，若 $A D = 16$ ， $C F = 6$ ，则 $P G + P H$ 的值为（）

A、6 B、8 C、10 D、16

查看试题解析

二、填空题

13. 计算： $(\frac{3 + \sqrt{3}}{\sqrt{3}}) (\sqrt{3} - 1) =$ ．

查看试题解析
14. 关于x的一元二次方程 $k x^{2} + 2 x - 1 = 0$ 有两个不相等的实数根，则k的最小整数是．

查看试题解析
15. 二次根式：已知 $a = 3 + 2 \sqrt{2}$ ， $b = 3 - 2 \sqrt{2}$ ，求 $a^{2} b - a b^{2} =$ ．

查看试题解析
16. 若 $x = \frac{1}{2}$ 是方程 $x^{2} - x + k = 0$ 的一个根，则 $k =$ ．

查看试题解析
17. 如图，四边形 $A B C D$ 是菱形，点O是对角线的交点，三条直线都经过点O，图中阴影面积为 $24 c m^{2}$ ，其中一条对角线长为 $6 c m$ ，则另一条对角线长为 $c m$ ．

查看试题解析
18. 如图，边长为6的正方形 $A B C D$ 绕点B按顺时针方向旋转30°后得到正方形 $B E F G$ ， $E F$ 交 $C D$ 于点H，则 $E H$ 的长为（结果保留根号）．

查看试题解析

三、解答题

19. 解方程：

(1)、 ${(5 x + 3)}^{2} - 4 = 0$

(2)、 $2 x^{2} - 3 x - 1 = 0$

(3)、 $2 {(x + 1)}^{2} = x (x + 1)$

查看试题解析
20. 计算：

(1)、 $(2 \sqrt{2} + \sqrt{6}) (3 \sqrt{2} - 2 \sqrt{6})$

(2)、 $\sqrt{\frac{1}{3}} \cdot (\sqrt{3} \cdot \sqrt{\frac{1}{3}}) + \sqrt{3}$

查看试题解析
21. 已知 $x = \sqrt{7} + \sqrt{5}$ ， $y = \sqrt{7} - \sqrt{5}$ ，求下列各式的值

(1)、 $x^{2} - x y + y^{2}$

(2)、 $\frac{x}{y} - \frac{y}{x}$ ．

查看试题解析
22. 阅读下面解方程的过程：
解方程 ${(^{} - 1)}^{2} - 5 (x^{2} - 1) + 4 = 0$ ．
设 $x^{2} - 1 = y$ ，则原方程可化为 $y^{2} - 5 y + 4 = 0$ ①，解得 $y_{1} = 1$ ， $y_{2} = 4$ ．
当 $y = 1$ 时， $x^{2} - 1 = 1$ ，解得 $x = \pm \sqrt{2}$ ；当 $y = 4$ 时， $x^{2} - 1 = 4$ ，解得 $x = \pm \sqrt{5}$ ．
故原方程的解为 $x_{1} = \sqrt{2}$ ， $x_{2} = - \sqrt{2}$ ， $x_{3} = \sqrt{5}$ ， $x_{4} = - \sqrt{5}$ ．
由方程得到①的过程，利用换元法达到简化方程的目的，体现了转化的数学思想．
解答下列问题：

(1)、利用换元法解方程： ${(x^{2} + x)}^{2} + 2 (x^{2} + x) - 8 = 0$ ；

(2)、 $R t Δ A B C$ 三边是a，b，c，若两直角边a，b满足 $(a + b) (a + b - 7) + 10 = 0$ ，斜边 $c = 4$ ，求 $R t Δ A B C$ 的面积．

查看试题解析
23. 已知：如图，在正方形 $A B C D$ 中，点E、F分别在 $B C$ 和 $C D$ 上， $A E = A F$ ．

(1)、求证： $B E = D F$ ；

(2)、连接 $A C$ 交 $E F$ 于点O，延长 $O C$ 至点G，使 $O G = O A$ ，连接 $E G$ 、 $F G$ ．判断四边形 $A E G F$ 是什么特殊四边形？并证明你的结论．

查看试题解析
24. 如图，在菱形 $A B C D$ 中， $A C$ 与 $B D$ 相交于点O，点E在边 $A B$ 上， $E F ⊥ B O$ ， $E G ⊥ A O$ ，垂足分别为点F，点G．

(1)、求证：四边形 $E F O G$ 是矩形；

(2)、若点E在边 $A B$ 上（不与两端点重合）移动，连接 $F G$ ，已知 $A C = 8$ ， $B D = 6$ ，求 $F G$ 的最小值．

查看试题解析
25. 如图，P是矩形 $A B C D$ 内一点， $A P ⊥ B P$ ， $C E ⊥ B P$ ，垂足为点E， $A P = B E$ ．

(1)、求证：矩形 $A B C D$ 是正方形；

(2)、延长 $E C$ 到点F，使 $C F = B E$ ，连接 $B F$ ， $D F$ ， $P D$ ．若正方形 $A B C D$ 的边长为3，求四边形 $P B F D$ 的面积．

查看试题解析