山东省烟台市福山区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

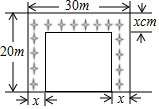
1. 若二次根式 $\sqrt{2 a - 4}$ 与 $\sqrt{2}$ 是同类二次根式，则a的值有可能是（）

A、 $6$ B、 $5$ C、 $4$ D、 $1$

查看试题解析
2. 使 $\frac{\sqrt{5 - x}}{x - 1}$ 有意义的实数x的取值范围是（）

A、 $x \leq 5$ B、 $x \leq 5$ 且 $x \neq 0$ C、 $x < 5$ 且 $x \neq 1$ D、 $x \leq 5$ 且 $x \neq 1$

查看试题解析
3. 下列计算正确的是（）

A、 $4 \sqrt{2} - 3 \sqrt{2} = 1$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{(1 - \sqrt{2})^{2}} = 1 - \sqrt{2}$ D、 $a \sqrt{x} - b \sqrt{x} = (a - b) \sqrt{x}$

查看试题解析
4. 下列结论：①若 $x^{2} = 16$ ，则 $x = 4$ ；②方程 $x (2 x - 1) = (2 x - 1)$ 的解为 $x = 1$ ；③若分式 $\frac{x^{2} - 3 x + 2}{x - 1}$ 的值为0，则 $x = 1$ 或 $x = 2$ ．正确的有（）

A、 $0$ 个 B、 $1$ 个 C、 $2$ 个 D、 $3$ 个

查看试题解析
5. 已知四边形 $A B C D$ 是平行四边形， $A C$ ， $B D$ 相交于点O，下列结论不正确的是（）

A、 $O A = O C$ ， $O B = O D$ B、当 $A B = C D$ 时，四边形 $A B C D$ 是菱形 C、当 $∠ A B C = 90 °$ 时，四边形 $A B C D$ 是矩形 D、当 $A C = B D$ 且 $A C ⊥ B D$ 时，四边形 $A B C D$ 是正方形

查看试题解析
6. 若x为实数，在 $(\sqrt{3} + 1) □ x$ 的“ $□$ ”中添上一种运算符号（在＋，－，×，÷中选择）后，其运算的结果是有理数，则x不可能的是（）

A、 $\sqrt{3} + 1$ B、 $\sqrt{3} - 1$ C、 $2 \sqrt{3}$ D、 $1 - \sqrt{3}$

查看试题解析
7. 某果园今年栽种果树 $300$ 棵，现计划扩大种植面积，使今后两年的栽种量都比前一年增长一个相同的百分数，这样三年（包括今年）的总栽种量为 $2100$ 棵.若这个百分数为 $x$ ，则由题意可列方程为（）

A、 $300 {(1 + x)}^{2} = 2100$ B、 $300 + 300 {(1 + x)}^{2} = 2100$ C、 $300 (1 + x) + 300 {(1 + x)}^{2} - 2100$ D、 $300 + 300 (1 + x) + 300 {(1 + x)}^{2} = 2100$

查看试题解析
8. 若方程 $(m + 3) x^{m^{2} - 7} + m x - 2 = 0$ 是关于x的一元二次方程，则m等于（）

A、 $\pm \sqrt{7}$ B、 $3$ C、 $- 3$ D、 $\pm 3$

查看试题解析
9. 已知x₁ ， x₂是一元二次方程x²﹣3x+1＝0的两实数根，则 $\frac{1}{1 - 3 x_{1}} + \frac{1}{1 - 3 x_{2}}$ 的值是（　　）

A、﹣7 B、﹣1 C、1 D、7

查看试题解析
10. 扬帆中学有一块长 $30 m$ ，宽 $20 m$ 的矩形空地，计划在这块空地上划出四分之一的区域种花，小禹同学设计方案如图所示，求花带的宽度．设花带的宽度为 $x m$ ，则可列方程为（）

A、 $(30 - x) (20 - x) = \frac{3}{4} \times 20 \times 30$ B、 $(30 - 2 x) (20 - x) = \frac{1}{4} \times 20 \times 30$ C、 $30 x + 2 \times 20 x = \frac{1}{4} \times 20 \times 30$ D、 $(30 - 2 x) (20 - x) = \frac{3}{4} \times 20 \times 30$

查看试题解析
11. 如图，点E在正方形 $A B C D$ 的边 $C D$ 上，将 $△ A D E$ 绕点A顺时针旋转 $90 °$ 到 $△ A B F$ 的位置，连接 $E F$ ，过点A作 $E F$ 的垂线，垂足为点H，与 $B C$ 交于点G.若 $B G = 3$ ， $C G = 2$ ，则 $C E$ 的长为（）

A、 $\frac{5}{4}$ B、 $\frac{15}{4}$ C、4 D、 $\frac{9}{2}$

查看试题解析
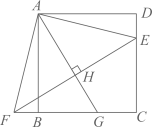12. 对于任意的正数m，n定义运算※为：m※n＝ ${\begin{matrix} \sqrt{m} - \sqrt{n} (m \geq n) \\ \sqrt{m} + \sqrt{n} (m < n) \end{matrix}$ 计算(3※2)×(8※12)的结果为（）

A、2－4 $\sqrt{6}$ B、2 C、2 $\sqrt{5}$ D、20

查看试题解析

二、填空题

13. 式子 $\sqrt{- x} + \frac{1}{\sqrt{x y}}$ 有意义，则点 $P (x ， y)$ 在第象限．

查看试题解析
14. 若关于x的一元二次方程 $k x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，则实数k的取值范围是．

查看试题解析
15. 对于实数m、n，定义算“♫”如下： $m$ ♫ $n = (m + n)^{2} - (m - n)^{2}$ ，若 $(a + 1)$ ♫ $(a - 2) = 16$ ，则 $a =$ ．

查看试题解析
16. 如图，矩形 $A B C D$ 中，点E，F分别是 $A B$ ， $C D$ 的中点，连接 $D E$ 和 $B F$ ，分别取 $D E$ ， $B F$ 的中点M，N．连接 $A M$ ， $C N$ ， $M N$ ．若 $A B = 2 \sqrt{2}$ ， $B C = 2 \sqrt{6}$ ，则图中阴影部分的面积为．

查看试题解析
17. 如图，在矩形 $A B C D$ 中， $A B = \sqrt{3}$ ．将 $∠ A$ 向内翻折，点A落在 $B C$ 上，记为 $A^{'}$ ，折痕为 $D E$ ．若将 $∠ B$ 沿 $E A^{'}$ 向内翻折，点B恰好落在 $D E$ 上，记为 $B^{'}$ ，则 $A D =$ ．

查看试题解析
18. 如图，菱形 $O A_{1} B_{1} C_{1}$ 中， $∠ A_{1} O C_{1} = 60 °$ ， $B_{1}$ 坐标为 $(2 ， 0)$ ，再以 $B_{1}$ 为对称中心作菱形 $O A_{2} B_{2} C_{2}$ ，再以 $B_{2}$ 为对称中心作菱形 $O A_{3} B_{3} C_{3}$ ，按此规律继续作下去，得到菱形 $O A_{n} B_{n} C_{n}$ ，则 $A_{n}$ 的坐标为．

查看试题解析

三、解答题

19. 计算

(1)、 $\sqrt{32} + 3 \sqrt{\frac{1}{2}} - 2 \sqrt{\frac{1}{8}}$

(2)、 $\sqrt{45} \div \sqrt{5} - \sqrt{\frac{1}{2}} \times \sqrt{8} + \sqrt{48}$

(3)、 $(\sqrt{5} - 3)^{2} + (\sqrt{11} + 3) (\sqrt{11} - 3)$

查看试题解析
20. 解方程：

(1)、2（x﹣1）²＝18；

(2)、x²﹣2x＝2x+1.

查看试题解析
21. 已知关于x的方程 $x^{2} - 4 x + k + 2 = 0$ 有两不相等的实数根．

(1)、求k的取值范围：

(2)、设方程两实数根分别为 $x_{1}$ ， $x_{2}$ ．且 $\frac{3}{x_{1}} + \frac{3}{x_{2}} = x_{1} x_{2} - 4$ ，求实数k的值．

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} - (m + 1) x + 3 m - 6 = 0$ ．

(1)、求证：方程总有两个实数根；

(2)、若方程有一个根是负数，求m的取值范围．

查看试题解析
23. 如图，在四边形 $A B C D$ 中， $A D / / B C$ ，点O是对角线 $A C$ 的中点，过点O作 $A C$ 的垂线，分别交 $A D$ 、 $B C$ 于点E、F．连接 $A F$ ， $C E$ ．试判断四边形 $A E C F$ 的形状，并证明．

查看试题解析
24. 某电子商店在销售某型号电话手表时，以高出进价的 $50 %$ 标价．已知按标价九折销售该型号电话手表8块与将标价直降100元销售7块获利相同．

(1)、求该型号电话手表每块进价和标价分别是多少元？

(2)、若该型号电话手表的进价不变，按（1）中的标价出售，该店平均每月可售出 $51$ 块，若每块电话手表每降价20元，每月可多售出3块．若希望尽量减少库存，每月获利要想达到 $26400$ 元．该型号电话手表每块应降价多少元？

查看试题解析
25. 小明在解决问题：已知a＝ $\frac{1}{2 + \sqrt{3}}$ ，求2a²－8a＋1的值，他是这样分析与解答的：
因为a＝ $\frac{1}{2 + \sqrt{3}}$ ＝ $\frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})}$ ＝2－ $\sqrt{3}$ ，

所以a－2＝－ $\sqrt{3}$ .

所以(a－2)²＝3，即a²－4a＋4＝3.

所以a²－4a＝－1.

所以2a²－8a＋1＝2(a²－4a)＋1＝2×(－1)＋1＝－1.

请你根据小明的分析过程，解决如下问题：

(1)、计算： $\frac{1}{\sqrt{2} + 1}$ = － .

(2)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}}$ ＋…＋ $\frac{1}{\sqrt{100} + \sqrt{99}}$ ；

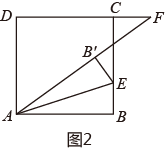
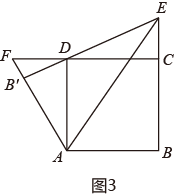
(3)、若a＝ $\frac{1}{\sqrt{2} - 1}$ ，求4a²－8a＋1的值.

查看试题解析
26. 如图，四边形 $A B C D$ 是正方形，点E在直线 $B C$ 上，连接 $A E$ 将 $△ A B E$ 沿 $A E$ 所在直线折叠，点B的对应点是点 $B^{'}$ ，连接 $A B^{'}$ 并延长直线 $D C$ 于点F．

(1)、当点F与点C重合时，如图1，试证明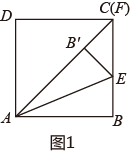： $D F + B E = A F$ ；

(2)、当点F在 $D C$ 的延长线上时，如图2，当点F在 $C D$ 的延长线上时，如图3，线段 $D F$ 、 $B E$ 、 $A F$ 有怎样的数量关系？请直接写出你的猜想，并选择一种情况给予证明．

查看试题解析