山东省威海市乳山市2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 下列二次根式中,与 是同类二次根式的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 若关于 的方程 没有实数根,则 的取值范围是( )A、 B、 C、 D、4. 若式子 有意义,则实数m的取值范围是( )A、m>﹣2 B、m>﹣2且m≠1 C、m≥﹣2 D、m≥﹣2且m≠15. 如图,正方形 的面积为 ,菱形 的面积为 ,则 , 两点间的距离为( )
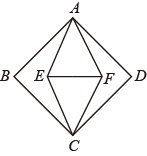 A、 B、 C、 D、6. 若 , 则( )A、1 B、 C、-7 D、或7. 对于方程 , 列表如下:
A、 B、 C、 D、6. 若 , 则( )A、1 B、 C、-7 D、或7. 对于方程 , 列表如下:……
……
则t的取值范围是( )
A、或 B、或 C、或 D、或8. 如果a,b是一元二次方程的两个实数根,那么( )A、 B、 C、 D、9. 将矩形纸片按图所示的方法进行折叠,得到等腰 , 若 , 则( ) A、 B、 C、 D、10. 如图,点O为矩形的对称中心,点E从点A出发沿向点B运动,到达点B处停止,延长交于点F,则四边形的形状变化依次为( )
A、 B、 C、 D、10. 如图,点O为矩形的对称中心,点E从点A出发沿向点B运动,到达点B处停止,延长交于点F,则四边形的形状变化依次为( ) A、平行四边形→菱形→平行四边形→菱形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→矩形→菱形→平行四边形 D、平行四边形→菱形→矩形→平行四边形
A、平行四边形→菱形→平行四边形→菱形 B、平行四边形→菱形→平行四边形→矩形 C、平行四边形→矩形→菱形→平行四边形 D、平行四边形→菱形→矩形→平行四边形二、多选题
-
11. 如图,不能判定为菱形的是( )
 A、 B、 C、 D、12. 如图,在正方形中, , 点E在边上,且 . 将沿对折至 , 点D落在正方形内部点F处,延长交边于点G,连接 , . 下列结论正确的是( )
A、 B、 C、 D、12. 如图,在正方形中, , 点E在边上,且 . 将沿对折至 , 点D落在正方形内部点F处,延长交边于点G,连接 , . 下列结论正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、三、填空题
-
13. 计算: .14. 如图,在矩形中,对角线与交于点O,过点A作 , 垂足为点E,若 , 则°.
 15. 若方程的两个实数根为a,b,则 .16. 如图在菱形 中, 是对角线 上一动点过点 作 于 . 于点 .若菱形 的周长为 ,面积为 ,则 的值为 .
15. 若方程的两个实数根为a,b,则 .16. 如图在菱形 中, 是对角线 上一动点过点 作 于 . 于点 .若菱形 的周长为 ,面积为 ,则 的值为 .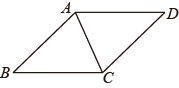 17. 如图,P是正方形内一点, , , , 则°.正方形的面积是 .
17. 如图,P是正方形内一点, , , , 则°.正方形的面积是 . 18. 已知 , 则 =
18. 已知 , 则 =四、解答题
-
19. 解方程: . (用十字相乘法求解)20. 计算: .21. 已知:四边形是平行四边形,以对角线为斜边作 , 连接 , , .

求证:四边形是矩形.
22. 关于x的方程的两个实数根是 , .(1)、求k的取值范围;(2)、若k为整数,且满足 , 求k的值.23. 已知: , 点E是上的一点,过点作 , 分别与 , , 交于点F,G,H. , . 将四边形放在平行线中,使其四个顶点分别落在直线 , , , 上.(1)、如图1,若四边形是正方形,且点D与G重合,则正方形的面积为; (2)、如图2,若四边形是菱形,且点A与点E重合,的延长线过点H,求菱形的面积.
(2)、如图2,若四边形是菱形,且点A与点E重合,的延长线过点H,求菱形的面积. 24. 【材料阅读】
24. 【材料阅读】材料一:在进行二次根式化简与运算时,有时会遇到形如的式子,可以通过分母有理化进行化简或计算.如化简: . 具体方法如下:
方法一: .
方法二: .
材料二:我们在学习分式时知道,对于公式可以逆用.即: .
【问题解决】
(1)、化简:;(2)、计算:;(3)、计算: .25. 【源模:模型建立】白日登山望峰火,黄昏饮马傍交河.——《古从军行》唐 李欣
诗中隐含着一个有趣的数学问题,我们称之为“将军饮马”问题.关键是利用轴对称变换,把直线同侧两点的折线问题转化为直线两侧的线段问题,从而解决距高和最短的一类问题.“将军饮马”问题的数学模型如图所示:

【新模1:模型应用】
如图1,正方形的边长为 , 点E在边上,且 , F为对角线上一动点,欲使周长最小.
 (1)、在图中确定点F的位置(要有必要的画图痕迹,不用写画法);(2)、周长的最小值为 .(3)、【新模2:模型变式】
(1)、在图中确定点F的位置(要有必要的画图痕迹,不用写画法);(2)、周长的最小值为 .(3)、【新模2:模型变式】如图2,在矩形中, , , 在矩形内部有一动点P,满足 , 则点P到A,B两点的距离和的最小值为 .
 (4)、【超模:模型拓广】
(4)、【超模:模型拓广】如图3, , , . 请构造合理的数学模型,并借助模型求的最小值.
