山东省青岛市崂山区2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 若m<n,则下列不等式不一定正确的是( )A、2m<2n B、m﹣n<0 C、m﹣3<m﹣2 D、m2<n22. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、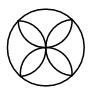 C、
C、 D、
D、 3. 下列各式从左到右是分解因式的是( )A、10x3y4=2xy•5x2y3 B、x2+3x﹣5=(x﹣1)(x+4)﹣1 C、(a﹣b)(a+b)=a2﹣b2 D、4a2﹣4ab+b2=(b﹣2a)24.
3. 下列各式从左到右是分解因式的是( )A、10x3y4=2xy•5x2y3 B、x2+3x﹣5=(x﹣1)(x+4)﹣1 C、(a﹣b)(a+b)=a2﹣b2 D、4a2﹣4ab+b2=(b﹣2a)24.已知,如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为( )
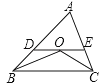 A、5 B、6 C、7 D、85. 不等式组 的解集是 ,那么m的取值范围( )A、 B、 C、 D、6. 已知:如图,点D,E分别在△ABC的边AC和BC上,与相交于点 , 给出下面四个条件:①∠1=∠2;②AD=BE;③④DF=EF,从这四个条件中选取两个,不能判定是等腰三角形的是( )
A、5 B、6 C、7 D、85. 不等式组 的解集是 ,那么m的取值范围( )A、 B、 C、 D、6. 已知:如图,点D,E分别在△ABC的边AC和BC上,与相交于点 , 给出下面四个条件:①∠1=∠2;②AD=BE;③④DF=EF,从这四个条件中选取两个,不能判定是等腰三角形的是( )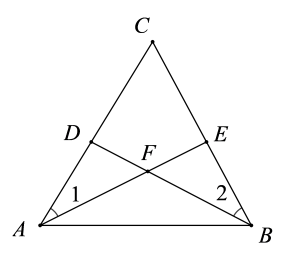 A、①② B、①④ C、②③ D、③④7. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( )
A、①② B、①④ C、②③ D、③④7. 如图,在△ABC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为( ) A、30° B、40° C、50° D、65°8. 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是点A(-3,0)、点B(-1,2)、点C(3,2).则到△ABC三个顶点距离相等的点的坐标是( )
A、30° B、40° C、50° D、65°8. 如图,在平面直角坐标系中,△ABC三个顶点的坐标分别是点A(-3,0)、点B(-1,2)、点C(3,2).则到△ABC三个顶点距离相等的点的坐标是( )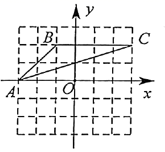 A、(0,-1) B、(0,0) C、(1,-1) D、(1,-2)
A、(0,-1) B、(0,0) C、(1,-1) D、(1,-2)二、填空题
-
9. 命题“等腰三角形两底角相等”的逆命题是。10. 关于x的不等式﹣2x+a≤2的解集如图所示,则a的值是 .
 11. 如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=
11. 如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=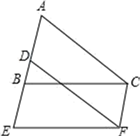 12. 如图,直线 : 与直线 : 相交于点 ,则关于x的不等式 的解集为.
12. 如图,直线 : 与直线 : 相交于点 ,则关于x的不等式 的解集为.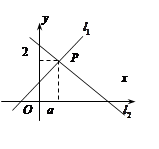 13. 如图,Rt△OCB的斜边在y轴上,OC= , 直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则坐标是 .
13. 如图,Rt△OCB的斜边在y轴上,OC= , 直角顶点C在第二象限,将Rt△OCB绕原点顺时针旋转120°后得到△OC′B′,则坐标是 .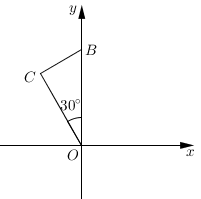 14. 如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置……,则正方形铁片连续旋转2020次后,点P的坐标为.
14. 如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置……,则正方形铁片连续旋转2020次后,点P的坐标为.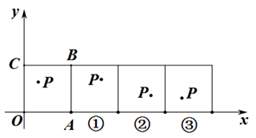 15. 崂山区某自行车店,新进单价为1200元的自行车,标价为每辆1680元.五一期间,进行打折促销活动,但是要保证利润率不低于5%,则最多可以打折.
15. 崂山区某自行车店,新进单价为1200元的自行车,标价为每辆1680元.五一期间,进行打折促销活动,但是要保证利润率不低于5%,则最多可以打折.三、解答题
-
16. 尺规作图:用直尺和圆规作图,不写作法,保留痕迹,线段a,h.求作:△ABC,使 , 且∠BAC=∠α,高AD=h.
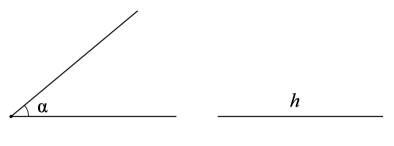 17. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(﹣3,2),B(﹣1,4),C(0,2).
17. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(﹣3,2),B(﹣1,4),C(0,2).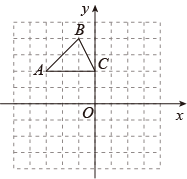
( 1 )将△ABC以顶点C为旋转中心旋转180°,画出旋转后对应的△A1B1C1;
( 2 )平移△ABC,若A的对应点A2的坐标为(5,﹣2),画出平移后的△A2B2C2;
( 3 )若将△A2B2C2绕某一点旋转可以得到△A1B1C1 , 请直接写出旋转中心的坐标.
18.(1)、因式分解x2(x﹣1)+4(1﹣x);(2)、因式分解(x+1)(x+2)+;(3)、解不等式组 , 并写出它的所有非负整数解.19. 如图,△ABC中,AB=AC,AD⊥AC交BC于点D,且∠CDA=60°,BD=2,求BC的长.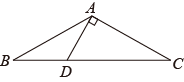 20. 如图,△ABC中,DE⊥BC于点E,交∠BAC的平分线AD于点D,过点D作DM⊥AB于点M,作DN⊥AC于点N,且BM=CN.求证:点E是BC的中点.
20. 如图,△ABC中,DE⊥BC于点E,交∠BAC的平分线AD于点D,过点D作DM⊥AB于点M,作DN⊥AC于点N,且BM=CN.求证:点E是BC的中点.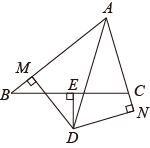 21. 某商场计划购进A,B两种新型节能台灯共120盏,这两种台灯的进价、售价如表所示:
21. 某商场计划购进A,B两种新型节能台灯共120盏,这两种台灯的进价、售价如表所示:类型
价格
进价(元/盏)
售价(元/盏)
A型
30
45
B型
50
70
(1)、若商场预计进货款为5200元,则这两种台灯各购进多少盏?(2)、若商场规定B型台灯的进货数量不超过A型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?22. 如图,△ACB与△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上的一点,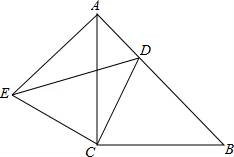 (1)、求证:△ACE≌△BCD;(2)、若DE=13,BD=12,求线段AB的长.23. 阅读理解并解答:(1)、我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式在运用完全平方公式行因式分解时,关键是判断这个多项式是不是一个完全平方式,同样地,把一个多项式进行部分因式分解可以解决代数式的值的最大(或最小)值问题.
(1)、求证:△ACE≌△BCD;(2)、若DE=13,BD=12,求线段AB的长.23. 阅读理解并解答:(1)、我们把多项式a2+2ab+b2及a2﹣2ab+b2叫做完全平方式在运用完全平方公式行因式分解时,关键是判断这个多项式是不是一个完全平方式,同样地,把一个多项式进行部分因式分解可以解决代数式的值的最大(或最小)值问题.例如:①x2+2x+3=(x2+2x+1)+2=(x+1)2+2,
∵(x+1)2是非负数,即(x+1)2≥0,
∴(x+1)2+2≥2.则这个代数式x2+2x+3的最小值是 , 这时相应的x的值是 .
②3x2﹣12x+5=3(x2﹣4x)+5=3(x2﹣4x+4﹣4)+5=3(x﹣2)2﹣12+5=3(x﹣2)2﹣7,
∵(x﹣2)2是非负数,即(x﹣2)2≥0,
∴3(x﹣2)2﹣7≥﹣7.
则这个代数式3x2﹣12x+5的最小值是 , 这时相应的x的值是 .
(2)、仿照上述方法求代数式﹣x2﹣14x+10的最大或最小值,并写出相应的x的值;(3)、实践应用:如图,工人师傅要在等腰直角△AEF的内部作一个矩形ABCD(矩形对边相等),其中AB和AD分别在两直角边上, ,∠DCB=90°.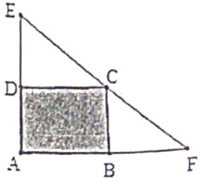
①如果设矩形的一边AB=xcm,那么AD边的长度为 cm;
②请用含x的代数式表示矩形ABCD的面积,求出当x取何值时,矩形ABCD的面积最大,最大值是多少?
24. 如图,△ABC是边长为6的等边三角形,P是AC边上一动点(与A,C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),连接PQ交AB于D.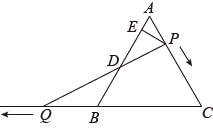 (1)、设AP的长为x,则PC= , QC=;(2)、当∠BQD=30°时,求AP的长;(3)、过点Q作QF⊥AB交AB延长线于点F,过点P作PE⊥AB交AB延长线于点E,则EP,QF有怎样的关系?说明理由;(4)、在运动过程中,线段ED的长是否发生变化?如果不变,求出线段ED的长
(1)、设AP的长为x,则PC= , QC=;(2)、当∠BQD=30°时,求AP的长;(3)、过点Q作QF⊥AB交AB延长线于点F,过点P作PE⊥AB交AB延长线于点E,则EP,QF有怎样的关系?说明理由;(4)、在运动过程中,线段ED的长是否发生变化?如果不变,求出线段ED的长