山东省临沂市沂南县2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

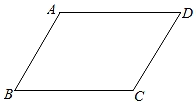
1. 使式子 $\sqrt{a - 2}$ 有意义的a的取值范围是（）

A、 $a > 2$ B、 $a \geq 2$ C、 $a \neq 2$ D、 $a \leq 2$

查看试题解析
2. 如图，在平行四边形ABCD中，∠B+∠D＝100°，则∠A等于（　　）

A、50° B、65° C、100° D、130°

查看试题解析
3. 下列根式是最简二次根式的是（）

A、 $\sqrt{0.6}$ B、 $\sqrt{6}$ C、 $\sqrt{60}$ D、 $\sqrt{\frac{1}{6}}$

查看试题解析
4. 以下列线段为边，不能组成直角三角形的是（）

A、1cm，1cm，2cm B、1cm，2cm， $\sqrt{3}$ cm C、3cm，4cm， $\sqrt{7}$ cm D、5cm，12cm，13cm

查看试题解析
5. 下列运算正确的是（）

A、 $\sqrt{3}$ ＋ $\sqrt{2}$ ＝ $\sqrt{5}$ B、 $\sqrt{3}$ × $\sqrt{2}$ ＝ $\sqrt{5}$ C、 $\frac{\sqrt{3}}{\sqrt{2}}$ ＝1 D、 $\sqrt{14}$ × $\sqrt{7}$ ＝7 $\sqrt{2}$

查看试题解析
6. 如图，在四边形ABCD中，对角线AC、BD相交于点O，下列选项不能判定四边形ABCD是平行四边形的是（）

A、AB＝DC，AD＝BC B、AB∥DC，AD＝BC C、AO＝CO，OB＝OD D、∠ABC＝∠ADC，∠DAB＝∠DCB

查看试题解析
7. 如图，在△ABC中，点D，E分别是AB，BC的中点，若△DBE的周长是7，则 $△ A B C$ 的周长（）

A、8 B、10 C、12 D、14

查看试题解析
8. 如图，正方形ABCD的边长为3，点P为对角线AC上任意一点，PQ⊥AB，垂足分别是E，Q，则BP的最小值为（）

A、3 $\sqrt{2}$ B、3 C、 $\frac{3 \sqrt{2}}{2}$ D、 $\frac{3}{2}$

查看试题解析
9. 如图，在▱ABCD中，连接AC，∠ABC=∠CAD=45°，AB＝1，则▱ABCD的周长是（）

A、2 $\sqrt{2}$ ＋2 B、2 $\sqrt{2}$ C、2 $\sqrt{3}$ ＋2 D、 $\sqrt{2}$ ＋2

查看试题解析
10. 如图，在▱ABCD中，AB＞AD，小于AD的长为半径画弧，分别交AB，F；再分别以点E，F为圆心 $\frac{1}{2}$ EF的长为半径画弧，两弧交于点G，则下列结论中不正确的是（）

A、AG平分∠DAB B、AD＝DH C、DH＝BC D、CH＝DH

查看试题解析
11. 如图，在2×2的方格中，小正方形的边长是1，则AC边上的高为（）

A、 $\frac{3 \sqrt{5}}{5}$ B、 $\frac{3}{2} \sqrt{2}$ C、 $\sqrt{5}$ D、 $\frac{3}{2}$

查看试题解析
12. 如图，在矩形ABCD中，O为AC中点， $E F ⊥ A C$ 交AB于E，点G是AE中点且∠AOG＝30°，下列结论：（1）DC＝3OG；（2）OG＝ $\frac{1}{2}$ BC；（3） $△ O G E$ 等边三角形；（4）S_△AOE＝ $\frac{1}{6}$ S_矩形ABCD ，正确的有（）

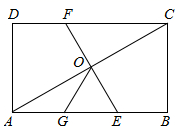A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 计算 $\sqrt{9 π}$ ＋ $\sqrt{25 π}$ 的结果为．

查看试题解析
14. 比较大小：2 $\sqrt{5}$ 3 $\sqrt{2}$ ．（填“＞”“＜”或“＝”）

查看试题解析
15. 如图，△ABC中，AD是高，E、F分别是AB、AC的中点，AB=10，AC＝6，则四边形AEDF的周长为．

查看试题解析
16. 如图，在平行四边形ABCD中，E、F分别是边AD、BC上一点，DE=BF，连接AC、EF、AF、CE，若AC=5，AE＝AF，EF＝8，则四边形AECF的面积为．

查看试题解析
17. 《九章算术》中有一个“折竹抵地”问题：“今有竹高九尺，末折抵地，去本三尺，折后竹尖抵地与竹子底部的距离为3尺，问折处高几尺？即：如图，BC＝3尺，则AC＝尺．

查看试题解析
18. 如图，在Rt△ABC中，∠BAC＝90°，∠ACB＝45°，AB＝2 $\sqrt{2}$ ，点P为BC上任意一点，以PA，PC为邻边作平行四边形PAQC，则PQ的最小值为．

查看试题解析

三、解答题

19. 计算：

(1)、2 $\sqrt{18}$ ﹣2 $\sqrt{\frac{1}{2}}$ ＋ $\sqrt{2}$ ．

(2)、（3 $\sqrt{48} - \sqrt{6}$ ）÷ $\sqrt{27}$ ．

查看试题解析
20. 已知如图，四边形ABCD中，∠B＝90°，AB= BC= $5 \sqrt{2}$ ， CD＝6，AD＝8，求四边形的面积

查看试题解析
21. 如图，在▱ABCD中，AE⊥BD，CF⊥BD，垂足分别为E、F，求证：AE＝CF．

查看试题解析
22. 笔直的河流一侧有一旅游地C，河边有两个漂流点A、B，其中AB=AC，由于某种原因，由C到A的路现在已经不通，为方便游客，决定在河边新建一个漂流点H(A，H，B在一条直线上)，并新修一条路CH，测得BC=5千米，CH=4千米，BH=3千米，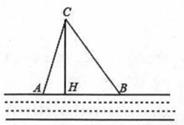

(1)、问CH是否为从旅游地C到河的最近的路线？请通过计算加以说明；

(2)、求原来路线AC的长。

查看试题解析
23. 如图，菱形ABCD的对角线AC、BD相交于点O ， E是AD的中点，点F、G在CD边上，EF⊥CD ， OG∥EF ．

(1)、求证：四边形OEFG是矩形；

(2)、若AD＝10，EF＝4，求CG的长．

查看试题解析
24. 在进行二次根式运算时，我们有时会碰上如 $\frac{2}{\sqrt{3} + 1}$ 这样的式子，我们还可以将其进一步化简： $\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 \times (\sqrt{3} - 1)}{2} = \sqrt{3} - 1$ 以上这种化简过程叫做分母有理化. $\frac{2}{\sqrt{3} + 1}$ 还可以尝试用以下方法化简：
$\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{{(\sqrt{3})}^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$

(1)、请用两种不同的方法化简； $\frac{2}{\sqrt{11} + 3}$

(2)、请任选一种方法化简： $\frac{3}{\sqrt{11} - 2 \sqrt{2}} - \frac{4}{\sqrt{15} - \sqrt{11}}$

查看试题解析
25. 如图1，已知在四边形ABCD中，AD∥BC，AB∥CD，BE平分∠ABC，交AD于点E，交BC于点F，O是BE的中点，连接OF，OC，OD．

(1)、求证：四边形ABFE是菱形；

(2)、若∠ABC＝90°，如图2所示：
①求证：∠ADO＝∠BCO；
②若∠EOD＝15°，AE＝1，求OC的长．

查看试题解析