山东省临沂市平邑县2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（　　）

A、 $\sqrt{20} = 2 \sqrt{10}$ B、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{12} \div 2 = 2 \sqrt{3}$

查看试题解析
2. 下列命题的逆命题是真命题的是（）

A、如果两个角是直角，那么它们相等 B、如果两个实数相等，那么它们的平方相等 C、如果一个四边形是菱形，那么它的四条边都相等 D、如果一个四边形是矩形，那么它的对角线相等

查看试题解析
3. 如图，在下列给出的条件中，能判定四边形ABCD为平行四边形的是（　　）

A、 $A B / / C D$ ， $A D ＝ B C$ B、 $∠ B A D ＝ ∠ A B C ， ∠ B C D ＝ ∠ A D C$ C、 $A B / / C D ， A B ＝ C D$ D、 $A B ＝ A D ， C B ＝ C D$

查看试题解析
4. 下列各组数中，以a，b，c为边的三角形不是直角三角形的是（）

A、a=1.5，b=2，c=3 B、a=7，b=24，c=25 C、a=6，b=8，c=10 D、a=5，b=12，c=13

查看试题解析
5. 如图，在 $R t Δ A B C$ 中， $∠ C ＝ 90 °$ ， $∠ A ＝ 3 0^{∘}$ ， E是 $A B$ 边的中点， $D E ⊥ A C$ 于点D，交 $A B$ 于点E，若 $A B ＝ 16$ ，则 $D E$ 的长是（　　）

A、 $8$ B、 $6$ C、 $4$ D、 $2$

查看试题解析
6. 如图2，在菱形ABCD中，对角线AC=4，∠BAD=120°，则菱形ABCD的周长为（）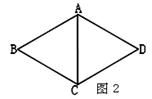

A、20 B、18 C、16 D、15

查看试题解析
7. 如图，在正方形ABCD的边BC的延长线上取一点E，使CE=AC连接AE交CD于点F，则∠AFC等于（）

A、112.5° B、120° C、135° D、145°

查看试题解析
8. 如图， $E ， F$ 分别是 $▱ A B C D$ 的边 $A D 、 B C$ 上的点， $E F ＝ 6$ ， $∠ D E F ＝ 60 °$ ，将四边形 $E F C D$ 沿 $E F$ 翻折，得到 $E F C^{'} D^{'}$ ， $E D^{'}$ 交 $B C$ 于点G，则 $Δ G E F$ 的周长为（　　）

A、 $6$ B、 $12$ C、 $18$ D、 $24$

查看试题解析
9. 如图(图在第二页)所示是一株美丽的勾股树，其中所有的四边形都是正方形，所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3，则最大正方形E的面积是（）

A、13 B、26 C、47 D、94

查看试题解析
10. 如图，在四边形 $A B C D$ 中， $∠ B ＝ 9 0^{∘}$ ， $A B ＝ B C ＝ 1$ ， $C D ＝ 6$ ， $A D ＝ 2$ ，若 $∠ D ＝ a$ ，则 $∠ B C D$ 的大小为（　　）

A、 $2 a$ B、 $90 ° + a$ C、 $135 ° ﹣ a$ D、 $180 ° ﹣ a$

查看试题解析
11. 如图，▱ABCD中，点O为对角线AC、BD的交点，点E为CD边的中点，连接OE，如果AB=4，OE=3，则▱ABCD的周长为（）

A、7 B、10 C、14 D、20

查看试题解析
12. 如图，在等腰直角 $Δ A B C$ 中， $∠ A C B ＝ 9 0^{∘}$ ， O是斜边 $A B$ 的中点，点 $D ， E$ 分别在直角边 $A C ， B C$ 上，且 $∠ D O E ＝ 90 °$ ， $Δ D O E$ 绕点O旋转， $D E$ 交 $O C$ 于点P，则下列结论：
① $A D + B E ＝ A C$ ；
② $A D^{2} + B E^{2} ＝ D E^{2}$ ；
③ $A B C$ 的面积等于四边形 $C D O E$ 面积的2倍；
④ $O D ＝ O E$ ．
其中正确的结论有（　　）

A、①④ B、②③ C、①②③ D、①②③④

查看试题解析

二、填空题

13. 若式子 $\frac{\sqrt{3 - x}}{3 x + 1}$ 有意义，则x的取值范围是．

查看试题解析
14. 矩形的两条对角线的夹角为 $60 °$ ，较短的边长为 $12 m$ ，则对角线长为cm．

查看试题解析
15. 如图，数轴上点A表示的实数是．

查看试题解析
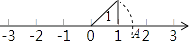16. 如图，边长分别为 $4$ 和 $8$ 的两个正方形 $A B C D$ 和 $C E F G$ 并排放在一起，连接 $B D$ 并延长交 $E G$ 于点T，交 $F G$ 于点P，则GT的长为．

查看试题解析
17. 如图，在菱形ABCD中，点E、F、G、H分别是AB、BC、CD、AD的中点，EF＝2EH，则AB与EH的数量关系是AB＝EH.

查看试题解析
18. 如图，在 $Δ A B C$ 中， $∠ B A C ＝ 4 5^{∘}$ ， $A B ＝ A C ＝ 8$ ， P为 $A B$ 边上一动点，以 $P A 、 P C$ 为边作平行四边形 $P A Q C$ ，则对角线 $P Q$ 的最小值为．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{32} + 2 \sqrt{\frac{1}{2}} - \sqrt{50}$ ；

(2)、 $(3 \sqrt{12} - 2 \sqrt{\frac{1}{3}} + \sqrt{48}) \div 2 \sqrt{3}$ ．

查看试题解析
20. 如图是一块四边形木板，其中 $A B = 16 cm$ ， $B C = 24 cm$ ， $C D = 9 cm$ ， $A D = 25 cm$ ， $∠ B = ∠ C = 90 °$ ．李师傅找到 $B C$ 边的中点 $P$ ，连接 $A P$ ， $D P$ ，发现 $△ A P D$ 是直角三角形．请你通过计算说明理由．

查看试题解析
21. 在△ABC中，AB＝15，BC＝14，AC＝13，求△ABC的面积．某学习小组经过合作交流，给出了下面的解题思路，请你按照他们的解题思路完成解答过程．作AD⊥BC于D，设BD＝x，用含x的代数式表示CD→根据勾股定理，利用AD作为“桥梁”，建立方程模型求出x→利用勾股定理求出AD的长，再计算三角形的面积．

查看试题解析
22. 如图，在 $Δ A B C$ 中， $∠ B A C ＝ 90 °$ ， $A D$ 是中线，E是 $A D$ 的中点，过点A作AF∥BC交BE的延长线于F，连接CF．

(1)、求证： $A D ＝ A F$ ；

(2)、如果 $A B ＝ A C$ ．试判断四边形 $A D C F$ 的形状，并证明你的结论．

查看试题解析
23. 如图，已知四边形 $A B C D$ 是平行四边形， $∠ B C D$ 的平分线 $C F$ 交边 $A B$ 于F， $∠ A D C$ 的平分线 $D G$ 交边 $A B$ 于C，且 $D G$ 与 $C F$ 交于点E．

(1)、求证： $A F ＝ B G$ ；

(2)、求证： $Δ E F G$ 是直角三角形；

(3)、在 $A B C D$ 中，添上一个什么条件使 $Δ E F G$ 是等腰直角三角形．（直接写出要添加的条件，不需要证明）

查看试题解析
24. 已知，在 $Δ A B C$ 中， $∠ B A C ＝ 90 °$ ， $∠ A B C ＝ 45 °$ ，点D为直线 $B C$ 上一动点（点D不与点 $B ， C$ 重合）．以 $A D$ 为边作正方形 $A D E F$ ，连接 $C F$ ．

(1)、如图 $1$ ，当点D在线段 $B C$ 上时．求证： $C F + C D ＝ B C$ ；

(2)、如图 $2$ ，当点D在线段 $B C$ 的延长线上时，其他条件不变，请直接写出 $C F ， B C ， C D$ 三条线段之间的关系；

(3)、如图3，当点D在线段 $B C$ 的反向延长线上时，且点 $A ， F$ 分别在直线 $B C$ 的两侧，其他条件不变；
①请直接写出 $C F ， B C ， C D$ 三条线段之间的关系；
②若正方形 $A D E F$ 的边长为 $2$ ，对角线 $A E ， D F$ 相交于点O，连接 $O C$ ．直接写出 $O C$ 的长度．

查看试题解析