山东省聊城市阳谷县2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 已知平行四边形ABCD中，∠A＋∠C＝110°，则∠B的度数为（）

A、125° B、135° C、145° D、155°

查看试题解析
2. 如图， $▱ A B C D$ 的对角线 $A C$ ， $B D$ 交于点O，若 $A C = 6$ ， $B D = 8$ ，则 $A B$ 的长可能是（）

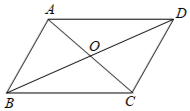A、10 B、8 C、7 D、6

查看试题解析
3. 如图，在四边形ABCD中，已知AB∥CD，添加一个条件，可使四边形ABCD是平行四边形．下列不正确的是（）

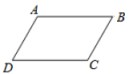A、BC∥AD B、BC=AD C、AB=CD D、∠A+∠B=180°

查看试题解析
4. 如图，在菱形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点O，若 $S_{菱形 A B C D} = 24$ ， $B D = 6$ ，则菱形 $A B C D$ 的周长是（）

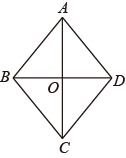A、5 B、10 C、20 D、40

查看试题解析
5. 若一个正方形的面积是12，则它的边长是（）

A、 $2 \sqrt{3}$ B、3 C、 $3 \sqrt{2}$ D、4

查看试题解析
6. 下列各数：－2，0， $\frac{1}{3}$ ， 0.020020002…（相邻两个2之间依次多一个0）， $π$ ，其中无理数的个数是（）

A、4 B、3 C、2 D、1

查看试题解析
7. 下列说法中正确的是（）．

A、0.09的平方根是0.3 B、 $\sqrt{16} = \pm 4$ C、0的立方根是0 D、1的立方根是 $\pm 1$

查看试题解析
8. 用不等式表示图中的不等式的解集，其中正确的是（）

A、 $x > - 2$ B、 $x < - 2$ C、 $- 2 < x < 2$ D、 $x > 2$

查看试题解析
9. 若x+2021>y+2021，则（）

A、x+2<y+2 B、x－2<y－2 C、2x<2y D、－2x<－2y

查看试题解析
10. 如果不等式3x﹣m≤0的正整数解为1，2，3，则m的取值范围是（）

A、9≤m＜12 B、9＜m＜12 C、m＜12 D、m≥9

查看试题解析
11. 在平面直角坐标系中，若点 $A (x + 3 ， \frac{2 x}{3} - 4)$ 在第四象限，则 $x$ 的取值范围是（）

A、 $- 3 < x < 6$ B、 $x < - 3$ C、 $x > 6$ D、 $3 < x < 6$

查看试题解析
12. 如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案．现有五种正方形纸片，面积分别是1，2，3，4，5，选取其中三块（可重复选取）按图的方式组成图案，使所围成的三角形是面积最大的直角三角形，则选取的三块纸片的面积分别是（）

A、1，4，5 B、2，3，5 C、3，4，5 D、2，2，4

查看试题解析

二、填空题

13. 已知矩形的对角线AC与BD相交于点O，若AO=1，那么BD= ．

查看试题解析
14. 如图，△ABC中，∠A＝73°，∠B＝45°，点D是AC的中点，点E是AB边上一点，且AE＝ $\frac{1}{2}$ AB，则∠ADE＝°．

查看试题解析
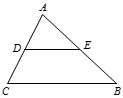15. 按一定规律排成的一列数依次为： $\frac{1}{2}$ ， $\frac{\sqrt{2}}{5}$ ， $\frac{\sqrt{3}}{10}$ ， $\frac{2}{17}$ ， $\frac{\sqrt{5}}{26}$ ， ……按此规律排下去，这列数中的第10个数是．

查看试题解析
16. 不等式组 ${\begin{array}{l} \frac{2 x - 1}{3} > 1 \\ x + 1 \geq 0 \end{array}$ 的最小整数解是．

查看试题解析
17. 设“●”、“▲”表示两种不同的物体，现用天平称（如图），若用x、y分别表示“●”、“▲”的重量，写出正确的不等式是．

查看试题解析
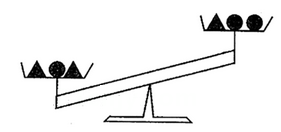18. 如图，△ABC的边BC在数轴上，点B对应的数字是1，点C对应的数字是2，∠ACB＝90°，AC＝2，以点B为圆心，AB为半径的圆弧交数轴于点D，则点D所表示的数为．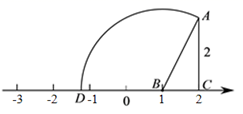

查看试题解析

三、解答题

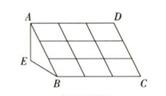
19. 已知一个正数m的两个不同的平方根是 $a - 1$ 与 $5 - 2 a$ ，求a和m的值．

查看试题解析
20. 如图，一菜农要修建蔬菜大棚，棚宽BE=2m，棚高AE=1.5m，长BC=18m.AE所在的墙面与地面垂直，现要在棚顶覆盖一种农用塑料薄膜，请你为他计算一下，共需多少这种塑料薄膜？

查看试题解析
21. 已知代数式2m-1与4m+5的积为正，和为负.

(1)、判断2m-1与4m+5的正负；

(2)、求m的取值范围.

查看试题解析
22. 如图，在▱ABCD 中，对角线 AC，BD 相交于点 O，过点 O 的一条直线分别交 AD，BC 于点 E，F．求证：AE=CF．

查看试题解析
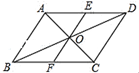23. 如图，在正方形ABCD中，点E，F在AC上，且AF=CE.求证：四边形BEDF是菱形.

查看试题解析
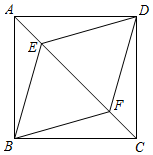24. 已知：如图，点D是△ABC中BC边上的中点，DE⊥AC ， DF⊥AB ，垂足分别是点EF ，且BF＝CE ．

(1)、求证：Rt△BDF≌Rt△CDE

(2)、问：△ABC满足什么条件时，四边形AEDF是正方形，并说明理由．

查看试题解析
25. 为了节能减排，我区某校准备购买某种品牌的节能灯，已知4只A型节能灯和5只B型节能灯共需55元，2只A型节能灯和1只B型节能灯共需17元.

(1)、求1只A型节能灯和1只B型节能灯的售价各是多少元？

(2)、学校准备购买这两种型号的节能灯共300只，要求A型节能灯的数量不超过B型节能灯的数量的2倍，请设计出最省钱的购买方案，并说明理由.

查看试题解析
26. 已知实数a，b，c在数轴上所对应的点分别为A，B，C，其中b是最小的正整数，且a，b，c满足 ${(c - 5)}^{2} + | a + 2 b | = 0$ ．两点之间的距离可用这两点对应的字母表示，如：点A与点B之间的距离可表示为AB．

(1)、 $a =$ ， $b =$ ， $c =$ ；

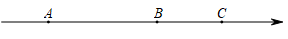(2)、点A，B，C开始在数轴上运动，若点A以每秒1个单位长度的速度向左运动，同时，点B以每秒2个单位长度的速度向右运动，点C以每秒5个单位长度的速度向右运动，假设运动时间为t秒，则 $A B =$ ， $B C =$ ；（结果用含t的代数式表示）这种情况下， $B C - A B$ 的值是否随着时间t的变化而改变？若变化，请说明理由；若不变，请求其值；

(3)、若A，C两点的运动和（2）中保持不变，点B 变为以每秒n（ $n > 0$ ）个单位长度的速度向右运动，当 $t = 3$ 时， $A C = 2 B C$ ，求n的值．

查看试题解析