山东省德州市陵城区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式中是二次根式的为（）

A、 $\sqrt{7}$ B、 $\sqrt{a}$ C、 $\sqrt[3]{8}$ D、 $\sqrt{- 3}$

查看试题解析
2. 下列运算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、3 $\sqrt{2} - \sqrt{2} = 3$ C、 $\sqrt{2} \times \sqrt{3} = \sqrt{6}$ D、 $\sqrt{6} \div \sqrt{3} = 2$

查看试题解析
3. 如图，在四边形ABCD中，下列条件不能判定四边形ABCD是平行四边形的是（）

A、AB∥DC， AD∥BC B、AB＝DC，AD＝BC C、AD∥BC，AB＝DC D、AB∥DC，AB＝DC

查看试题解析
4. 下列满足条件的三角形中，不是直角三角形的是（）

A、三内角之比为1∶2∶3 B、三边长的平方之比为1∶2∶3 C、三边长之比为3∶4∶5 D、三内角之比为3∶4∶5

查看试题解析
5. 已知实数 $a$ 在数轴上的对应点位置如图所示，则化简 $| a - 1 | - \sqrt{{(a - 2)}^{2}}$ 的结果是（）

A、 $3 - 2 a$ B、 $- 1$ C、1 D、 $2 a - 3$

查看试题解析
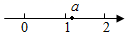6. 如图，正方形ABCD的面积是（）

A、5 B、25 C、7 D、1

查看试题解析
7. 如图，矩形ABCD的两条对角线相交于点O，∠AOB＝60°，AO＝4，则AB的长是（）

A、4 B、5 C、6 D、8

查看试题解析
8. 如图，网格中每个小正方形的边长均为1，点A，B，C都在格点上，以A为圆心，AB为半径画弧，交最上方的网格线于点D，则CD的长为（）

A、 $\sqrt{5}$ B、0.8 C、 $3 - \sqrt{5}$ D、 $\sqrt{13}$

查看试题解析
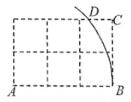9. 如图，已知E是正方形ABCD对角线AC上一点，且AB=AE，则∠DBE度数是（）

A、15° B、32.5° C、22.5° D、30°

查看试题解析
10. 如图，在矩形 $O A B C$ 中，点B的坐标是 $(1 ， 3)$ ，则 $A C$ 的长是（）

A、3 B、 $2 \sqrt{2}$ C、 $\sqrt{10}$ D、4

查看试题解析
11. 如图，▱ABCD的对角线相交于点O，且 $A B \neq A D$ ，过点O作 $O E ⊥ B D$ 交BC于点E，若 $△ C D E$ 的周长为10，则▱ABCD的周长为 $($ $)$

A、14 B、16 C、20 D、18

查看试题解析
12. 如图，正方形ABCD的面积为144，菱形BCEF面积为108，则△ABF面积为（）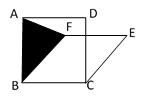

A、18 B、36 C、18 $\sqrt{7}$ D、36 $\sqrt{7}$

查看试题解析

二、填空题

13. 已知 $\sqrt{a + 9}$ 是最简二次根式，且它与 $\sqrt{32}$ 是同类二次根式，则a = ．

查看试题解析
14. 已知y＝ $\sqrt{2 x - 1} - \sqrt{1 - 2 x}$ +8x，则 $\sqrt{4 x + 5 y - 6}$ 的算术平方根为．

查看试题解析
15. 如图，为了检查平行四边形书架ABCD的侧边是否与上、下边都垂直，工人师傅用一根绳子比较了其对角线AC，BD的长度，若二者长度相等，则该书架的侧边与上、下边都垂直，请你说出其中的数学原理．

查看试题解析
16. 如图，要为一段高5m，长13m的楼梯铺上红地毯，至少需要红地毯m.

查看试题解析
17. 如图所示的网格是正方形网格，△ $A B C$ 和△ $C D E$ 的顶点都是网格线交点，那么∠ $B A C +$ ∠ $C D E =$ °．

查看试题解析
18. 如图，在等边三角形ABC中，BC＝6cm，射线AG∥BC，点E从点A出发沿射线AG以1cm/s的速度运动，点F从点B出发沿射线BC以2cm/s的速度运动．如果点E、F同时出发，设运动时间为t(s)当t＝s时，以A、C、E、F为顶点四边形是平行四边形．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{2} + \sqrt{4} - \sqrt{8}$ ；

(2)、 $(\sqrt{12} - \sqrt{\frac{1}{3}}) \times \sqrt{6}$ ．

查看试题解析
20. 已知a＝ $\sqrt{2}$ ＋1，b＝ $\sqrt{2}$ ﹣1，求下列各式的值．

(1)、a²＋2ab＋b²；

(2)、a²﹣b²

查看试题解析
21. 如图1，已知在△ABC中，CD⊥AB于D．BC＝20，AC＝15，AD＝9

(1)、求CD的长．

(2)、求AB的长．

查看试题解析
22. 阅读下面的材料，然后解答问题：
我们新定义一种三角形，两边的平方和等于第三边平方的2倍的三角形叫做奇异三角形．

(1)、理解并填空：
①根据奇异三角形的定义，请你判断：等边三角形一定是奇异三角形吗？（填“是”或“不是”）
②若某三角形的三边长分别为1、 $\sqrt{7}$ 、2，则该三角形（填“是”或“不是”）奇异三角形．

(2)、探究：在 $R t Δ A B C$ 中，两边长分别是 $a ， c$ ，且 $a^{2} = 50$ ， $c^{2} = 100$ ，则这个三角形是否是奇异三角形？请说明理由．

查看试题解析
23. 如图，在 $▱ A B C D$ 中，过点 $D$ 作 $D E ⊥ A B$ 于点 $E$ ，点 $F$ 在边 $C D$ 上， $C F = A E$ ，连接 $A F$ ， $B F$ ．

(1)、求证：四边形 $B F D E$ 是矩形；

(2)、已知 $∠ D A B = 60 °$ ， $A F$ 是 $∠ D A B$ 的平分线，若 $A D = 3$ ，求 $D C$ 的长度．

查看试题解析
24. 如图，▱ABCD中，AB=2cm，AC=5cm，S▱_ABCD=8cm² ， E点从B点出发，以1cm每秒的速度，在AB延长线上向右运动，同时，点F从D点出发，以同样的速度在CD延长线上向左运动，运动时间为t秒．

(1)、在运动过程中，四边形AECF的形状是；

(2)、t＝时，四边形AECF是矩形；

(3)、求当t等于多少时，四边形AECF是菱形．

查看试题解析
25. 如图1，已知在四边形ABCD中，AD∥BC，AB∥CD，BE平分∠ABC，交AD于点E，交BC于点F，O是BE的中点，连接OF，OC，OD．

(1)、求证：四边形ABFE是菱形；

(2)、若∠ABC＝90°，如图2所示：
①求证：∠ADO＝∠BCO；
②若∠EOD＝15°，AE＝1，求OC的长．

查看试题解析