山东省滨州市滨城区2020-2021学年八年级下学期期中数学试题

试卷更新日期：2022-03-21 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式是二次根式的是（　　）

A、 $\sqrt{- 3}$ B、 $\sqrt{2}$ C、 $\sqrt[3]{3}$ D、 $\sqrt{3 - π}$

查看试题解析
2. 下列计算正确的是（）

A、 $\sqrt{2} \times \sqrt{5} = \sqrt{10}$ B、 ${(\sqrt{2})}^{2} = 4$ C、 $\sqrt{{(- 4)}^{2}} = 2$ D、 $\sqrt{6} \div \sqrt{2} = 3$

查看试题解析
3. 在直角三角形中，若两条边的长分别是1cm、2cm，则第三边的长为（）

A、3cm B、 $\sqrt{5}$ cm C、2cm或 $\sqrt{5}$ cm D、 $\sqrt{3}$ cm或 $\sqrt{5}$ cm

查看试题解析
4. 如图，在 $Δ A B C$ 中， $∠ A C B = 90 °$ ， D是 $A B$ 的中点， $D E ⊥ B C$ ， E为垂足， $A C = \frac{1}{2} A B$ ，图中为 $60 °$ 的角有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
5. 在下列给出的条件中，能判定四边形ABCD为平行四边形的是（）

A、AB＝BC ， CD＝DA B、AB//CD ， AD＝BC C、AB//CD ， ∠A＝∠C D、∠A＝∠B ， ∠C＝∠D

查看试题解析
6. 若最简二次根式 $\sqrt{7 a + b}$ 与 $\sqrt[b + 3]{6 a - b}$ 可合并则 $a b$ 的值为（）

A、2 B、-2 C、-1 D、1

查看试题解析
7. 在下列四组线段中，能组成直角三角形的是（）

A、 $a = 3^{2} ， b = 4^{2} ， c = 5^{2}$ B、 $a = 11 ， b = 12 ， c = 13$ C、 $a ： b ： c = 1 ： 1 ： 2$ D、 $a = 5 ， b = 12 ， c = 13$

查看试题解析
8. 下列说法正确的是（）

A、对角线相等且相互平分的四边形是矩形 B、对角线相等且相互垂直的四边形是菱形 C、四条边相等的四边形是正方形 D、对角线相互垂直的四边形是平行四边形

查看试题解析
9. 如图，▱ABCD的对角线相交于点O，且AB≠AD，过点O作OE⊥BD交BC于点E．若△CDE的周长为8cm，则▱ABCD的周长为（）

A、8cm B、12cm C、16cm D、24cm

查看试题解析
10. 如图，将一个边长和宽分别为8，4的长方形纸片ABCD折叠，使C点与A点重合，则折痕BE的长是（　　　　）

A、3 B、4 C、5 D、6

查看试题解析
11. 如图，菱形ABCD的对角线相交于点O ， AC＝12，BD＝16，点P为边BC上一点，且点P不与点B、C重合．过点P作PE⊥AC于点E ， PF⊥BD于点F ，连结EF ，则EF的最小值为（）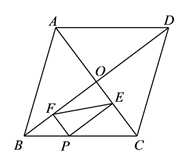

A、4 B、4.8 C、5 D、6

查看试题解析
12. 如图，正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，下列结论：①BE＝DF，②∠DAF＝15°，③AC垂直平分EF，④BE+DF＝EF，⑤S_△CEF＝S_△ABE+S_△ADF，其中正确的结论有（　　）个．

A、5 B、4 C、3 D、2

查看试题解析

二、填空题

13. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
14. 如图，在 $▱ A B C D$ 中， $∠ B = 50 °$ ，则 $∠ D =$ ．

查看试题解析
15. 如图，为估计池塘两岸边A，B两点间的距离，在池塘的一侧选取点O，分别去OA、OB的中点M，N，测的MN=32 m，则A，B两点间的距离是m.

查看试题解析
16. 如图：已知 $▱ A B C D$ 的对角线 $A C 、 B D$ 相交于点O， $A C = 24$ cm， $B D = 38$ cm， $A D = 14$ cm，那么 $△ O B C$ 的周长为cm．

查看试题解析
17. 如图，在菱形ABCD中，对角线AC与BD相交于点O，AC＝8，BD＝6，OE⊥AD于点E，交BC于点F，则EF的长为．

查看试题解析
18. 如图，在四边形 $A B C D$ 中，点E、F分别是线段AD、BC的中点，G、H分别是线段BD、AC的中点，当四边形 $A B C D$ 的边满足时，四边形 $E G F H$ 是菱形.

查看试题解析
19. 观察下列各式： $\frac{1}{\sqrt{2} + 1} = \sqrt{2} - 1$ ， $\frac{1}{\sqrt{3} + \sqrt{2}} = \sqrt{3} - \sqrt{2}$ ， $\frac{1}{\sqrt{4} - \sqrt{3}} = \sqrt{4} - \sqrt{3}$ ， …，从计算结果中找出规律，并利用这一规律计算： $(\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ \frac{1}{\sqrt{2021} + \sqrt{2020}}) (\sqrt{2021} + 1) =$ ．

查看试题解析
20. 如图，在矩形 $A B C D$ 中，O为 $A C$ 中点， $E F$ 过O点且 $E F ⊥ A C$ 分别交 $D C$ 于F，交 $A B$ 于E，点G是 $A E$ 中点且 $∠ A O G = 30 °$ ，则下列结论正确的是．
（1） $D C = 3 O G$ ；（2） $O G = \frac{\sqrt{3}}{3} B C$ ；（3） $Δ O G E$ 是等边三角形；（4） $S_{Δ A O E} = \frac{1}{6} S_{矩形 A B C D}$ ．

查看试题解析

三、解答题

21.

(1)、 $(4 \sqrt{2} - 3 \sqrt{6}) \div 2 \sqrt{2} + {(\sqrt{2021})}^{0} + | \sqrt{3} - 1 |$

(2)、 $(\sqrt{3} + 1) (\sqrt{3} - 1) + {(\sqrt{6} - 1)}^{2}$

查看试题解析
22.

(1)、已知a＝3+2 $\sqrt{2}$ ，b＝3﹣2 $\sqrt{2}$ ，求代数式a²b﹣ab²的值.

(2)、化简求值： $(\frac{x^{2} + 4}{x^{2} - 4} - \frac{2}{x - 2}) \div \frac{x}{2}$ ，其中x＝ $\sqrt{2}$ ﹣2.

查看试题解析
23. 如图，等边△ABC的边长是2，D，E分别为AB，AC的中点，延长BC至点F，使CF＝ $\frac{1}{2}$ BC，连结CD和EF.

(1)、求证：四边形CDEF是平行四边形；

(2)、求四边形BDEF的周长.

查看试题解析
24. 观察、思考与验证

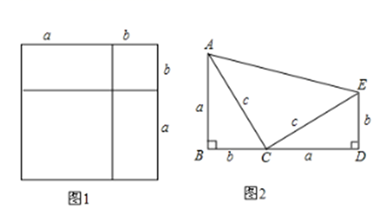(1)、如图1是一个重要公式的几何解释，请你写出这个公式 .

(2)、如图2所示，∠B=∠D=90°，且B，C，D在同一直线上.试说明：∠ACE=90°.

(3)、伽菲尔德（1881年任美国第20届总统）利用（1）中的公式和图2证明了勾股定理（发表在1876年4月1日的<新英格兰教育日志》上），请你写出验证过程.

查看试题解析
25. 如图，BD是△ABC的角平分线，过点作DE $//$ BC交AB于点E ， DF $//$ AB交BC于点F ．

(1)、求证：四边形BEDF是菱形；

(2)、若∠ABC＝60°，∠ACB＝45°，CD＝6，求菱形BEDF的边长．

查看试题解析
26. 如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 5$ ， $B C = 3$ ，点P从点A出发，以每秒2个单位长度的速度沿折线 $A - C - B - A$ 运动．设点P的运动时间为t秒 $(t > 0)$ ．

(1)、求AC的长及斜边AB上的高．

(2)、当点P在CB上时，
①CP的长为（用含t的代数式表示）．

②若点P在 $∠ B A C$ 的角平分线上，则t的值为．

(3)、在整个运动过程中，直接写出 $△ B C P$ 是等腰三角形时t的值．

查看试题解析