江西省宜春市高安市2020-2021学年八年级下学期期中数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 下列各组数中是勾股数的是( )A、1, , B、 , , C、 , , D、 , ,2. 若是二次根式,则x的值不可能是( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 四边形的对角线 , 交于点O,下列条件中,能判定四边形为正方形的是( )A、 , B、 , , C、 , D、 , ,5. 如图,▱ABCD的对角线AC与BD相交于点O,且∠OCD=90°.若E是BC边的中点,BD=10,AC=6,则OE的长为( )
 A、1.5 B、2 C、2.5 D、36. 如图,由10根完全相同的小棒拼接而成,请你再添2根与前面完全相同的小棒,拼接后的图形恰好有3个菱形的方法共有( )
A、1.5 B、2 C、2.5 D、36. 如图,由10根完全相同的小棒拼接而成,请你再添2根与前面完全相同的小棒,拼接后的图形恰好有3个菱形的方法共有( ) A、3种 B、4种 C、5种 D、6种
A、3种 B、4种 C、5种 D、6种二、填空题
-
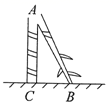
7. 若一直角三角形的两边长为4、5,则第三边的长为8. 已知 , 则的值为 .9. 《九章算术》中有一个“折竹抵地”问题:“今有竹高九尺,末折抵地,去本三尺,问折者高几何?”意思是:现有竹子高9尺,折后竹尖抵地与竹子底部的距离为3尺,问折处高几尺?即:如图,AB+AC=9尺,BC=3尺,则AC=尺.
 10. 如图,在菱形 中, ,点E在 上,若 ,则 .
10. 如图,在菱形 中, ,点E在 上,若 ,则 .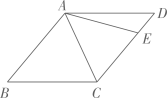 11. 如图,在正方形中, , 点E为边的中点,P为对角线上一动点,则的最小值为 .
11. 如图,在正方形中, , 点E为边的中点,P为对角线上一动点,则的最小值为 . 12. 矩形中, , , E为射线上一动点,连接 , 将沿折叠,当点D的对应点落在矩形的对称轴上时,线段的长为 .
12. 矩形中, , , E为射线上一动点,连接 , 将沿折叠,当点D的对应点落在矩形的对称轴上时,线段的长为 .三、解答题
-
13.(1)、计算:(2)、如图,在中,E,F是对角线上的两点,且 , 求证: .
 14. 如图,在 中, , ,点 是 边上一点, , .
14. 如图,在 中, , ,点 是 边上一点, , .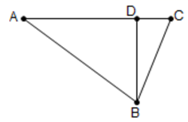 (1)、求证: ;(2)、若点 是 边上的动点,连接 ,求线段 的最小值.15. 有一道题:已知 , 求式子的值.
(1)、求证: ;(2)、若点 是 边上的动点,连接 ,求线段 的最小值.15. 有一道题:已知 , 求式子的值.小明同学的解答如图:
解:
第①步
第②步
第③步
第④步
第⑤步
(1)、小明同学的解答从第步开始出现不正确的,不正确的原因是;(2)、请你写出符合题意解答过程.16. 已知矩形中,点F在边上,四边形是平行四边形,请仅用无刻度的直尺分别按下列要求画图(保留画图痕迹,不写画法).(1)、在图1中作出线段的中点P; (2)、在图2中画出的中线 .
(2)、在图2中画出的中线 . 17. 在学习了《勾股定理》和《二次根式》后,数学学习小组进行了以“已知三角形三边的长度,求三形面积”为主题的探究活动,遇到了一道题:已知中, , , , 求的面积.
17. 在学习了《勾股定理》和《二次根式》后,数学学习小组进行了以“已知三角形三边的长度,求三形面积”为主题的探究活动,遇到了一道题:已知中, , , , 求的面积. (1)、小明同学想到了利用正方形网格构造三角形来求面积.如图是的正方形网格,每个小正方形顶点称为格点,边长均为 . 请你帮小明在网格中画出这个 , 要求三个顶点都在格点上,并直接写出的面积: .(2)、小华同学想到了课本第16页“阅读与思考”介绍了的求三角形面积公式,其中a、b、c为三角形的三边,:①(海伦公式);②(秦九韶公式).请你选用其中一个公式求出这个的面积.18. 仔细观察图形,认真分析各式,然后解答问题:
(1)、小明同学想到了利用正方形网格构造三角形来求面积.如图是的正方形网格,每个小正方形顶点称为格点,边长均为 . 请你帮小明在网格中画出这个 , 要求三个顶点都在格点上,并直接写出的面积: .(2)、小华同学想到了课本第16页“阅读与思考”介绍了的求三角形面积公式,其中a、b、c为三角形的三边,:①(海伦公式);②(秦九韶公式).请你选用其中一个公式求出这个的面积.18. 仔细观察图形,认真分析各式,然后解答问题:
(Ⅰ) , , , , ……
(Ⅱ) , , , ……
(1)、按以上规律,推算出;(2)、若其中一个三角形的面积是 , 则它是第个三角形;(3)、按以上规律,用含n(n是正整数)的等式表示: , ;(4)、试求出的值.19. 如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.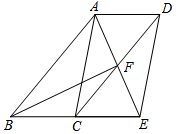 (1)、求证:BE=CD;(2)、若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.20. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”.
(1)、求证:BE=CD;(2)、若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.20. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“美丽三角形”. (1)、如图,在中, , , 求证:是“美丽三角形”;(2)、在中, , , 若是“美丽三角形”,求的长.21. 如图,中, , cm,cm,若动点P从点A出发,以每秒1cm的速度沿折线运动,设运动时间为t秒 .
(1)、如图,在中, , , 求证:是“美丽三角形”;(2)、在中, , , 若是“美丽三角形”,求的长.21. 如图,中, , cm,cm,若动点P从点A出发,以每秒1cm的速度沿折线运动,设运动时间为t秒 .
 (1)、当点P在边的垂直平分线上时,求t的值;(2)、当点P在的平分线上时,求t的值.22. 如图,矩形中,垂直平分对角线 , 分别交 , 于点E,F,垂足为O.
(1)、当点P在边的垂直平分线上时,求t的值;(2)、当点P在的平分线上时,求t的值.22. 如图,矩形中,垂直平分对角线 , 分别交 , 于点E,F,垂足为O. (1)、求证:四边形为菱形;(2)、若 , , 求四边形的面积;(3)、在(2)的条件下,求线段的长.23.(1)、【知识感知】如图1,我们把对角线互相垂直的四边形叫做垂美四边形,在我们学过的:①平行四边形②矩形③菱形④正方形中,能称为垂美四边形是;(只填序号)
(1)、求证:四边形为菱形;(2)、若 , , 求四边形的面积;(3)、在(2)的条件下,求线段的长.23.(1)、【知识感知】如图1,我们把对角线互相垂直的四边形叫做垂美四边形,在我们学过的:①平行四边形②矩形③菱形④正方形中,能称为垂美四边形是;(只填序号) (2)、【概念理解】如图2,在四边形中, , , 问四边形是垂美四边形吗?请说明理由.
(2)、【概念理解】如图2,在四边形中, , , 问四边形是垂美四边形吗?请说明理由. (3)、【性质探究】如图1,垂美四边形的两对角线交于点O,试探究 , , , 之间有怎样的数量关系?写出你的猜想,并给出证明;
(3)、【性质探究】如图1,垂美四边形的两对角线交于点O,试探究 , , , 之间有怎样的数量关系?写出你的猜想,并给出证明; (4)、【性质应用】如图3,分别以的直角边和斜边为边向外作正方形和正方形 , 连接 , , , 已知 , , 求长.
(4)、【性质应用】如图3,分别以的直角边和斜边为边向外作正方形和正方形 , 连接 , , , 已知 , , 求长.