江西省南昌市十校2020-2021学年第二学期期中联考八年级数学试题
试卷更新日期:2022-03-21 类型:期中考试
一、单选题
-
1. 由下列长度组成的各组线段中,不能组成直角三角形的是( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 若 <0,则 的结果是( ).A、0 B、-2 C、0或-2 D、24. 下列命题中正确的是( )A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且平分的四边形是正方形5. 如图,若将四根木条钉成的矩形木框变形为平行四边形 的形状,并使得其面积变为原矩形面积的一半,则平行四边形 的内角 的大小为( )
 A、100° B、120° C、135° D、150°6. 如图,已知圆柱底面的周长为 ,圆柱的高为 ,在圆柱的侧面上,过点 和点 嵌有一圈金属丝,则这圈金属丝的周长最小为( )
A、100° B、120° C、135° D、150°6. 如图,已知圆柱底面的周长为 ,圆柱的高为 ,在圆柱的侧面上,过点 和点 嵌有一圈金属丝,则这圈金属丝的周长最小为( )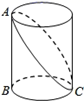 A、 B、 C、 D、7. 如图,在由10个完全相同的正三角形构成的网格图中,连接 .有下列结论:① ;② 是直角三角形;③ .其中,正确结论的个数为( )
A、 B、 C、 D、7. 如图,在由10个完全相同的正三角形构成的网格图中,连接 .有下列结论:① ;② 是直角三角形;③ .其中,正确结论的个数为( ) A、0 B、1 C、2 D、38. 如图,已知四边形中,分别为上的点(不与端点重合).下列说法不正确的是( )
A、0 B、1 C、2 D、38. 如图,已知四边形中,分别为上的点(不与端点重合).下列说法不正确的是( )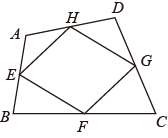 A、若分别为各边的中点,则四边形是平行四边形: B、若四边形是任意矩形,则存在无数个四边形是菱形 C、若四边形是任意菱形,则存在无数个四边形是矩形 D、若四边形是任意矩形,则至少存在一个四边形是正方形
A、若分别为各边的中点,则四边形是平行四边形: B、若四边形是任意矩形,则存在无数个四边形是菱形 C、若四边形是任意菱形,则存在无数个四边形是矩形 D、若四边形是任意矩形,则至少存在一个四边形是正方形二、填空题
-
9. 若 , 则 .10. 如图,数轴上点A表示的实数是 .
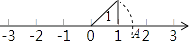 11. 如图,已知在中, , 分别以为直径作半圆,面积分别记为则等于 .
11. 如图,已知在中, , 分别以为直径作半圆,面积分别记为则等于 .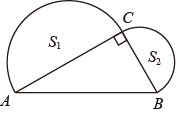 12. 如图,菱形的边长为 , 点E为边的中点,点P为对角线上一动点,则的最小值为 .
12. 如图,菱形的边长为 , 点E为边的中点,点P为对角线上一动点,则的最小值为 . 13. 如图,和都是等腰直角三角形,的顶点A在的斜边上,若 , 则的长为 .
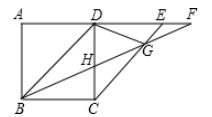
13. 如图,和都是等腰直角三角形,的顶点A在的斜边上,若 , 则的长为 . 14. 如图,正方形中,在的延长线上取点使 , 连接分别交于 , 下列结论:
14. 如图,正方形中,在的延长线上取点使 , 连接分别交于 , 下列结论:①;②;③;④图中有8个等腰三角形.
其中正确的有 (填序号),
三、解答题
-
15. 计算:16. 已知 , 求代数式的值.17. 如图,中, , 求的长.
 18. 如图,矩形纸片中,现把矩形纸片沿对角线折叠,点C与重合,求的长.
18. 如图,矩形纸片中,现把矩形纸片沿对角线折叠,点C与重合,求的长. 19. 在图①②中,点E在矩形ABCD的边BC上,且BE=AB,现要求仅用无刻度的直尺分别按下列要求画图.[保留画(作)图痕迹,不写画(作)法]
19. 在图①②中,点E在矩形ABCD的边BC上,且BE=AB,现要求仅用无刻度的直尺分别按下列要求画图.[保留画(作)图痕迹,不写画(作)法]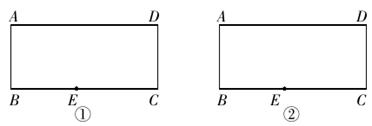 (1)、在图①中,画∠BAD的平分线;(2)、在图②中,画∠BCD的平分线.20. 已知 满足 .(1)、求 的值;(2)、判断以 为边的三角形的形状.21. 如图,中,点分别为的中点,连接并延长到点E,使 .
(1)、在图①中,画∠BAD的平分线;(2)、在图②中,画∠BCD的平分线.20. 已知 满足 .(1)、求 的值;(2)、判断以 为边的三角形的形状.21. 如图,中,点分别为的中点,连接并延长到点E,使 . (1)、求证:四边形AEBD是矩形;(2)、当满足什么条件时,矩形是正方形?证明你的结论.22. 如图,在中,分别在和的延长线上, , 求的长.
(1)、求证:四边形AEBD是矩形;(2)、当满足什么条件时,矩形是正方形?证明你的结论.22. 如图,在中,分别在和的延长线上, , 求的长.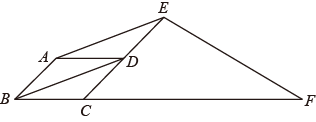 23. 如图1,四边形是正方形,点分别在上,点G在的延长线上,且 .
23. 如图1,四边形是正方形,点分别在上,点G在的延长线上,且 . (1)、求证:
(1)、求证:①;
②;
(2)、以线段为边作出正方形 , 连接猜想并写出四边形是怎样的特殊四边形,并证明你的猜想.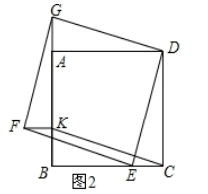 24. 如图,菱形中, , 点E从点D出发,以的速度沿射线运动,同时点F从点A出发,以的速度沿射线运动,连接和设运动时间为 .(1)、当时,如图①所示,则;
24. 如图,菱形中, , 点E从点D出发,以的速度沿射线运动,同时点F从点A出发,以的速度沿射线运动,连接和设运动时间为 .(1)、当时,如图①所示,则; (2)、当分别在线段和上时,如图②所示,求证:是等边三角形;
(2)、当分别在线段和上时,如图②所示,求证:是等边三角形; (3)、在(2)的条件下,连接交于点若求的长和此时t的值.25. 【探索发现】
(3)、在(2)的条件下,连接交于点若求的长和此时t的值.25. 【探索发现】如图①,将沿中位线折叠,使点A的对称点D落在边上,再将和分别沿折叠,使点均落在点D处,折痕形成一个四边形 . 小刚在探索这个问题时发现四边形是矩形.

小刚是这样想的:
 (1)、请参考小刚的思路写出证明过程;(2)、连接 , 当时,直接写出线段的数量关系;(3)、[理解运用]
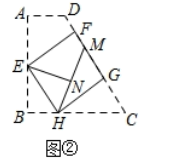
(1)、请参考小刚的思路写出证明过程;(2)、连接 , 当时,直接写出线段的数量关系;(3)、[理解运用]如图②,在四边形中, , 点E为的中点,把四边形折叠成如图②所示的正方形 , 顶点落在点M处,顶点落在点N处,求的长;
 (4)、[拓展迁移]
(4)、[拓展迁移]如图③,在四边形中, , 点分别为边的中点,将四边形沿直线折叠,使点A与B重合,点D落在处,将沿折叠,点C落在点处.判断四边形的形状,并求四边形的面积.
