2022年高考物理压轴题预测之动量守恒和能量守恒压轴题

试卷更新日期：2022-03-21 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 如图所示，在光滑水平面上放置一个质量为 $M$ 的滑块，滑块的一侧是一个 $\frac{1}{4}$ 弧形凹槽 $O A B$ ，凹槽半径为 $R$ ， A点切线水平。另有一个质量为 $m$ 的小球以速度 $v_{0}$ 从A点冲上凹槽，重力加速度大小为 $g$ ，不计摩擦。下列说法中正确的是（）

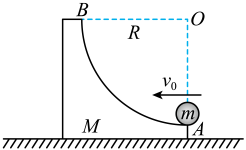A、当 $v_{0} = \sqrt{2 g R}$ 时，小球能到达 $B$ 点 B、如果小球的初速度足够大，球将从滑块的左侧离开滑块后落到水平面上 C、当 $v_{0} = \sqrt{2 g R}$ 时，小球在弧形凹槽上运动的过程中，滑块的动能一直增大 D、若小球能到达 $B$ 点，当到达 $B$ 点时滑块速度大小为 $\frac{m v_{0}}{M}$

查看试题解析
2. 动能回收系统能够提高电动车的续航能力，在电动车刹车瞬间，电源与电动车的电动机断开，同时启动动能回收系统，车轮带动电机转动向蓄电池充电，实现动能的回收，下列说法正确的是（）

A、动能回收技术应用了电磁感应的原理 B、动能回收技术应用了磁场对电流的驱动原理 C、如果关闭此系统，刹车时汽车的机械能守恒 D、随着技术的进步，动能回收的效率可以达到100%

查看试题解析

二、多选题

3. 如图所示，A、 $B$ 两物体的质量比 $m_{A} ： m_{B} = 4 ： 3$ ，它们原来静止在足够长的平板车C上，A、 $B$ 间有一根被压缩了的弹簧，地面光滑。当弹簧突然释放后，且已知A、 $B$ 组成的系统动量守恒。则有（）

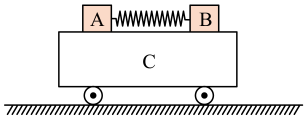A、A与C的动摩擦因数小于 $B$ 与C的动摩擦因数 B、任意时刻A、 $B$ 速率之比为 $3 ： 4$ C、最终稳定时小车向右运动 D、A、 $B$ 、C系统动量守恒

查看试题解析
4. 如图所示， $B C D$ 为竖直面内的光滑绝缘轨道，其中 $B C$ 段水平， $C D$ 段为半圆形轨道，轨道连接处均光滑，整个轨道处于竖直向上的匀强电场中，场强大小为 $E = \frac{2 m g}{q}$ ，一质量为 $M$ 的光滑绝缘斜面静止在水平面上，其底端与平面由微小圆弧连接。一带电量为 $- q$ 的金属小球甲，从距离地面高为 $H$ 的 $A$ 点由静止开始沿斜面滑下，与静止在 $C$ 点的不带电金属小球乙发生弹性碰撞。已知甲、乙两小球材质大小均相同，质量均为 $m$ ，且 $M = 2 m$ ，水平轨道足够长，不考虑两球之间的静电力，小球与轨道间无电荷转移， $g$ 取 $10 m / s^{2}$ ，则（）

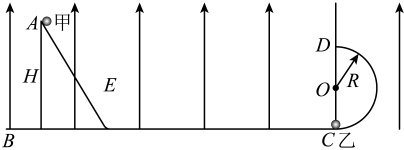A、甲球滑到斜面底端时斜面的速度大小为 $\sqrt{g H}$ B、甲、乙两球碰撞后甲的速度大小 $\sqrt{g H}$ C、甲、乙两球碰撞后乙的速度大小 $\sqrt{2 g H}$ D、若乙球恰能过 $D$ 点，半圆形轨道半径为 $\frac{2}{5} H$

查看试题解析
5. 如图所示，固定斜面足够长，斜面与水平面的夹角 $α = 37 °$ ，一质量为 $3 m$ 的L形工件沿斜面以速度 $v_{0} = 1 m / s$ 匀速向下运动。工件上表面光滑，下端为挡板，现将一质量为m的小木块轻轻放在工件上的A点，当木块运动到工件下端时（与挡板碰前的瞬间），工件速度刚好减为零，而后木块与挡板第一次相碰，以后木块将与挡板发生多次碰撞．已知木块与挡板都是弹性碰撞且碰撞时间极短，木块始终在工件上运动，重力加速度g取 $10 m / s^{2}$ ，下列说法正确的是（）

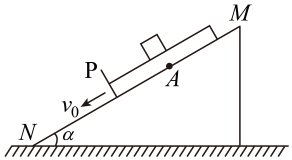A、下滑过程中，工件和木块系统沿斜面方向上动量不守恒 B、下滑过程中，工件的加速度大小为 $2 m / s^{2}$ C、木块与挡板第1次碰撞后瞬间，工件的速度大小为 $1.5 m / s$ D、木块与挡板第1次碰撞至第2次碰撞的时间间隔为 $0.75 s$

查看试题解析

三、综合题

6. 如图所示，半径 $R = 0.4 m$ 的光滑四分之一圆轨道放在光滑水平地面，其左侧紧靠竖直墙壁，底端切线水平长木板 $Q$ 的左端紧靠圆轨道（但不栓连），且上表面与圆轨道末端相切，长木板上放一个轻弹簧，轻弹簧右端被固定在木板的右端，长木板最左端放一物块 $P$ 。现从高于圆轨道顶端 $H = 2.8 m$ 的位置无初速释放一个质量 $m_{0} = 1.0 k g$ 的小球，小球无碰撞进入圆轨道，经过圆轨道后与物块 $P$ 发生碰撞，碰后小球返回到圆轨道的最高点时被锁定，小球被锁定的位置和圆轨道圆心的连线与竖直方向夹角 $θ = 60 °$ 。物块 $P$ 被碰后，沿长木板上表面向右滑动，随后开始压缩弹簧，已知最后物块 $P$ 刚好返回到长木板 $Q$ 的最左端。小球和物块 $P$ 都可以视作质点，物块 $P$ 与木板 $Q$ 的质量分别为 $m_{P}$ 和 $m_{Q}$ ， $m_{P} = m_{Q} = 2 k g$ ，取 $g = 10 m / s^{2}$ ，试求：

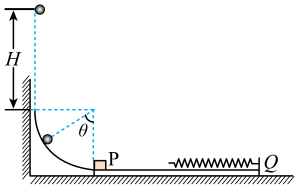(1)、小球在圆轨道上下滑的整个运动过程中，对轨道的水平冲量 $I$ 的大小；

(2)、小球与物块 $P$ 发生的碰撞中损失的机械能；

(3)、整个过程中轻弹簧的最大弹性势能。

查看试题解析
7. 如图，光滑水平面上有一矩形长木板A和静止的滑块C，滑块B置于A的最左端（滑块B、C均可视为质点）。若木板A和滑块B一起以 $v_{0} = 5 m / s$ 的速度向右运动，A与C发生时间极短的碰撞后粘在一起。已知木板A与滑块B间的动摩擦因数 $μ = 0.1$ ，且 $m_{A} = 2 k g$ ， $m_{B} = 1 k g$ ， $m_{C} = 2 k g$ ， g取 $10 m / s^{2}$ ，求：

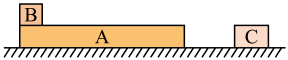(1)、长木板A与滑块C碰撞后瞬间，滑块C的速度大小；

(2)、B最终与A相对静止时速度的大小；

(3)、要使滑块B不从木板A上滑下，木板A至少多长。

查看试题解析
8. 如图所示，一条带有圆轨道的长轨道水平固定，圆轨道竖直，底端分别与两侧的直轨道相切，半径 $R = 0.5 m$ ，物块A以 $v_{0} = 6 m / s$ 的速度滑入圆轨道，滑过最高点Q，再沿圆轨道滑出后，与直轨上P处静止的物块B碰撞，碰后粘在一起运动。P点左侧轨道光滑，右侧轨道呈粗糙段、光滑段交替排列，每段长度都为 $L = 0.1 m$ 。物块与各粗糙段间的动摩擦因数都为 $μ = 0.1$ ， A，B的质量均为 $m = 1 k g$ （重力加速度g取 $10 m / s^{2}$ ；A，B视为质点，碰撞时间极短）。

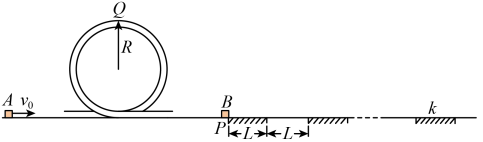(1)、求A滑过Q点时的速度大小v和受到的弹力大小F；

(2)、若碰后AB最终停止在第k个粗糙段上，求k的数值；

查看试题解析
9. 如图所示，在竖直平面内，粗糙水平面PQ左侧与四分之一光滑圆弧轨道在P点相切，右侧与水平面成θ = 30°的足够长传送带在Q点平滑连接。水平面PQ长L = 1.0m，圆弧半径R = 0.95m，皮带轮逆时针转动速率v = 3.0m/s。物块B停在Q点，现从光滑圆弧最高点将物块A由静止释放，经过P点运动到Q点，与B发生弹性碰撞。之后，A、B又发生多次弹性碰撞，最终A停在某一位置。A与B的碰撞时间忽略不计，两物块都可视为质点，其质量m_A = m_B = 1.0kg，物块A与PQ间动摩擦因数μ₁ = 0.15，物块B与传送带间的动摩擦因数 $μ_{2} = \frac{\sqrt{3}}{3}$ ，取g = 10m/s²。求：

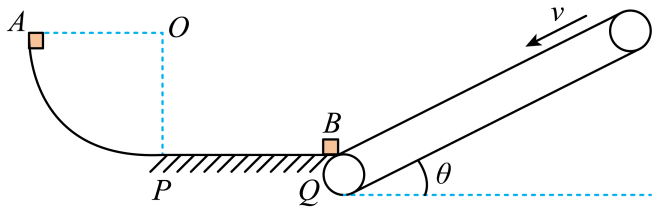(1)、物块A对P点压力的最大值F_N；

(2)、从物块A、B第一次碰撞后到第二次碰撞前，物块B在传送带上的运行时间t；

(3)、物块A在PQ上运动的总路程S；

(4)、物块B和传送带之间摩擦产生的总热量Q。

查看试题解析
10. 如图所示，是某种轨道玩具的结构示意图，弹射装置可以将小滑块以不同初速度弹出，经光滑水平轨道 $A B$ 、光滑圆弧轨道 $B C B'$ 、粗糙水平轨道 $B' D$ 、冲上光滑斜面轨道 $D E$ ，并从 $E$ 点沿水平方向飞出，最终落在水平轨道上。已知弹射器的最大弹性势能 $E_{p m a x} = 0.8 J$ ，圆弧轨道半径 $R = 10 c m$ ，水平轨道 $B' D$ 长 $L = 20 c m$ ，斜面轨道 $E$ 点距离水平轨道的高度 $h = 5 c m$ ，若小滑块可视为质点，其质量 $m = 0.1 k g$ ，与水平轨道 $B' D$ 的摩擦因数 $μ = 0.3$ ，其它阻力均不计，轨道各部分平滑连接，小滑块从 $E$ 点飞离前始终未脱离轨道， $g$ 取 $10 m / s^{2}$ 。

(1)、求小滑块被弹出的最大速度 $v_{m a x}$ ；

(2)、某次游戏中小滑块被弹出后，恰能够通过圆弧轨道最高点，求此次弹射弹射器的弹性势能 $E_{p}$ ；

(3)、将小滑块以不同初速度弹出，若均能沿轨道从 $E$ 点水平飞出，求小滑块最终在水平轨道上的落点到 $E$ 点的水平距离 $x$ 与弹射时弹射器的弹性势能满足的关系。

查看试题解析
11. 如图所示，足够长的平行光滑金属导轨竖直固定放置，导轨间距 $L = 0.5 m$ 。两金属棒 $a b$ 、 $c d$ 均垂直于导轨放置且与导轨接触良好，其长度恰好等于导轨间距，两棒的质量均为 $m = 0.2 k g$ ，金属棒 $a b$ 电阻 $R_{1} = 0.2 Ω$ ，金属棒 $c d$ 电阻 $R_{2} = 0.3 Ω$ ，回路中其余电阻忽略不计。 $c d$ 棒放置在水平绝缘平台上，整个装置处在垂直于导轨平面向里的匀强磁场中，磁感应强度 $B = 1 T$ 。棒 $a b$ 在恒力 $F$ 作用下由静止开始向上运动。当棒 $a b$ 上升距离为 $x = 2 m$ 时，它达到最大速度 $v_{m}$ ，此时 $c d$ 棒对绝缘平台的压力恰好为零。 $g$ 取 $10 m / s^{2}$ ，求：

(1)、恒力 $F$ 的大小；

(2)、 $a b$ 棒达到的最大速度 $v_{m}$ ；

(3)、在此过程中通过 $a b$ 棒的电荷量 $q$ ；

(4)、在此过程中 $c d$ 棒产生的焦耳热。

查看试题解析
12. 空间飞行器的交汇对接是载人航天中的一项基础技术。北京时间2021年9月20日，天舟三号货运飞船采用自主交会对接模式成功的和天和核心舱完成对接。成功对接后组合体沿圆形轨道运行，经过时间t，组合体绕地球转过的弧度为θ。地球半径为R，地球表面重力加速度为g，引力常量为G，不考虑地球自转。求：

(1)、组合体运动的周期T；

(2)、组合体所在圆轨道离地高度H；

(3)、已知天舟三号飞船在对接过程中的某一时刻质量为m，发动机喷气孔打开，在极短的时间内向后喷射出质量为Δm的燃气，喷出的燃气相对喷气后飞船的速度为v，求喷气后火箭增加的速度Δv。

查看试题解析
13. 如图所示光滑的轨道ABCD竖直放置，其圆形轨道部分半径R，轨道左侧A处放有弹射装置，被弹出的滑块可平滑进入轨道，轨道右端出口D恰好水平，且与圆心0等高，出口D的右侧接水平直轨道，轨道星光滑段、粗糙段交替排列，每段长度均为L。在第一个光滑段与粗糙段的结合处E位置放一质量m的滑块乙，质量为m的滑块甲通过弹射装置获得初动能。两滑块与各粗糙段间的动摩擦因数均为μ，弹簧的弹性势能与压缩量的平方成正比，当弹射器中的弹簧压缩量为d时，滑块甲恰好到达圆轨道内侧与圆心O等高处的C点，逐渐增大弹簧的压缩量，滑块甲与滑块乙会在E处发生碰撞（碰撞时间极短），碰后粘在一起运动，空气阻力忽略不计。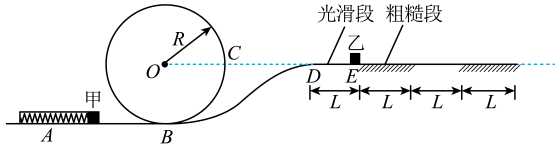

(1)、当弹射器中的弹簧压缩量为d时，求滑块甲经过B点时对管道的压力大小F_N；

(2)、当弹射器中的弹簧压缩量为2d时，滑块甲与滑块乙碰后粘在一起运动，求碰撞前后的机械能损失∆E；

(3)、若发射器中的弹簧压缩量为kd，求两滑块一起滑行的距离s与k的关系式。

查看试题解析
14. 如图为某游戏装置的示意图，由固定的竖直光滑圆弧轨道A、静止在光滑水平面上的滑板B、固定竖直挡板C组成。轨道A的底端与滑板B的上表面水平相切，初始时轨道A与滑板B左端紧靠在一起，滑板B右端与竖直挡板C相距 $d = 5 m$ 。游客乘坐滑椅（可视为质点）从轨道A上P点由静止出发，冲上滑板B，滑板B足够长（滑椅不会从滑板表面滑出），滑板B与挡板碰撞无机械能损失。已知游客与滑椅的总质量 $m = 100 k g$ ，圆弧轨道的半径 $R = 6.4 m$ ， O点为圆弧轨道的圆心， $O P$ 与竖直方向夹角 $θ = 60 °$ ，滑板B的质量 $M = 300 k g$ ，滑椅与滑板B间的动摩擦因数 $μ = 0.2$ ，空气阻力可忽略。求：

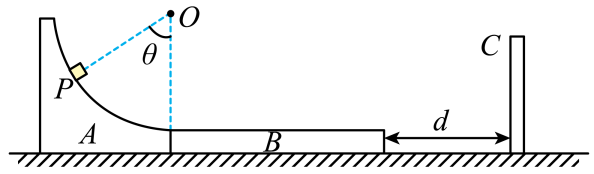(1)、游客与滑椅滑到圆弧轨道最低点时的动量大小；

(2)、滑板B与竖直挡板碰撞前，游客、滑椅和滑板B组成的系统产生的内能；

(3)、若滑板B右端与固定挡板C距离d可以改变，并要求滑板B只与挡板C碰撞两次，则d应满足的条件。

查看试题解析
15. 2022年2月4日将在北京举办第24届冬季奥运会，促生了许多室内冰雪项目。如图，与水中面成 $θ = 37 °$ 的光滑倾斜冰面，长L=75m、宽均为d=60m，两侧均安装有安全护网，底部有缓冲装置（未画出）。开始时，工作人员将载有一对父子的凹形滑板置于顶端正中间，由静止释放，瞬间父亲沿水中方向推出儿子，父子俩迅速分开，沿冰面滑下，若父亲及滑板总质量为M=70kg，儿子及滑板总质量为m=35kg，父子俩均视为质点，不计一切阻力，重力加速度g取10m/s² ， sin37°=0.6.假设运动中始终没有碰到护网。则：

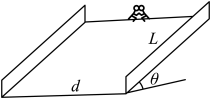(1)、若父子俩都能安全到达冰面底端，下滑过程支持力对父亲的冲量是多大；

(2)、父子俩都能安全到达冰面底端，父亲在推儿子时最多做功多少焦耳。

查看试题解析
16. 冰壶运动是北京冬奥会的主要项目之一。运动员把冰壶沿水平冰面投出让冰壶在冰面上自由滑行，在不与其他冰壶碰撞的情况下最终停在远处的某个位置。按比赛规则，投掷冰壶运动员的队友可以用毛刷在冰壶滑行前方来回摩擦冰面减小冰面的动摩擦因数以调节冰壶的运动。已知标准冰壶质量均为19.10kg，冰壶与冰面间的动摩擦因数均为μ=0.01，投掷线与0点间的距离为30m，取g=10m/s² ，整个过程中将冰壶视为质点。运动员在其滑行前方摩擦冰面后，冰壶和冰面的动摩擦因数变为原来的80%。（计算结果均保留到小数点后两位）

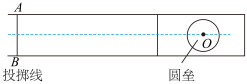(1)、若运动员以3.4m/s的速度将标准冰壶投出，其队友在冰壶自由滑行10m后开始在其滑行前方摩擦冰面，若前进中不与其他冰壶相碰，该冰壶还能滑行多远？

(2)、若运动员以3.0m/s的速度将标准冰壶从投掷线投出，这次投出后在滑行前方摩擦了6m长的冰面，该冰壶与对方置于圆垒中心处的蓝色冰壶发生正碰，碰撞可认为是弹性碰撞。碰后标准冰壶本应立即停下。但实际情况是通过电子测速设备发现该冰壶的速度为0.01m/s。经分析，由于制造工艺上的不足实际比赛中两冰壶质量是有偏差的，根据比赛的观测计算出蓝冰壶的质量。

查看试题解析
17. 如图所示，质量为 $m = 6 k g$ 的小物块B（可视为质点）放在质量为 $M = 2 k g$ 的木板A的最左端，A和B一起以 $v_{0} = 2 m / s$ 的速度在光滑水平面上向右运动，一段时间后A与右侧一竖直固定挡板P发生弹性碰撞。AB之间动摩擦因数 $μ = 0.1$ ，取重力加速度 $g = 10 m / s^{2}$ ，求：

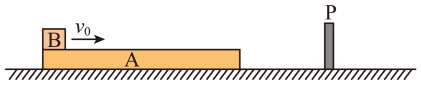(1)、木板A与挡板P第一次碰撞后木板A向左运动的最远距离 $s_{A}$ ；

(2)、木板A与挡板P第一次碰撞后到第二次碰撞前A、B的相对位移 $Δ s_{1}$ ；

(3)、木板A与挡板P第n次碰撞后到第 $n + 1$ 次碰撞前的时间间隔 $Δ T_{n}$ ；

(4)、要保证小物块B始终未从木板A上滑下，求木板A长度的最小值。

查看试题解析
18. 如图所示，物块A、B的质量分别为 $m_{A} = 1 k g ， m_{B} = 0.6 k g$ ， A静止在水平面上，与左侧固定挡板的距离为 $l$ 。物块B向左运动，当B与A的距离为s时，B的速度为 $v_{0} = 9 m / s$ ，经过 $1 s$ 与A相碰．A、B与地面的动摩擦因数分别为 $μ_{A} = 0.5$ ， $μ_{B} = 0.1$ 且A、B均可看作质点，所有碰撞时间极短且没有机械能损失，g取 $10 m / s^{2}$ 。求：

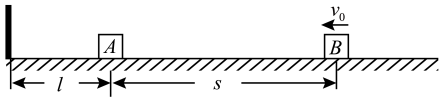(1)、物块B与A的距离s；

(2)、当 $l$ 取何值时，物块A和B会发生第二次碰撞。

查看试题解析
19. 如图，水平轻质弹簧的一端固定在墙壁上，处于自然状态时另一端在水平地面上的O点，O点左侧地面光滑，右侧粗糙。小物块P（与弹簧不拴接）在外力作用下将弹簧压缩至某一位置静止时，弹簧的弹性势能 $E_{p} = 45 J$ 。撤去外力，P被弹出后与静止在M点的小物块Q发生弹性正碰（碰撞时间极短）。已知P、Q的质量分别为 $m_{1} = 1 k g$ 、 $m_{2} = 5 k g$ ， P、Q与右侧地面间的动摩擦因数均为 $μ = 0.45$ ， O、M间的距离 $s = 1 m$ ，取重力加速度大小 $g = 10 m / s^{2}$ 。

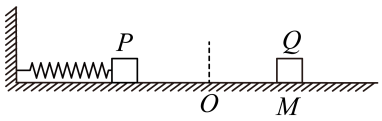(1)、求P第一次经过O点时的速度大小；

(2)、求P在M点与Q碰后瞬间的速度大小；

(3)、通过计算分析P、Q能否发生第二次碰撞。

查看试题解析