选择性必修二 5.3 导数在研究函数中的应用函数的极值

试卷更新日期：2022-03-20 类型：同步测试

进入出卷网下载

一、单选题

1. 若 $x = 1$ 是函数 $f (x) = (x^{2} + a x - 1) e^{x - 1}$ 的极值点，则 $f (x)$ 的极大值为（）

A、-1 B、 $- 2 e^{- 3}$ C、 $5 e^{- 3}$ D、1

查看试题解析
2. 已知函数 $f (x) = e^{- x} - e^{x} - x^{3} + 2 x - 1$ ，下列说法中正确的个数是（）
①函数 $f (x)$ 的图象关于点 $(0 ， - 1)$ 对称；

②函数 $f (x)$ 由三个零点；

③ $x = 0$ 是函数 $f (x)$ 的极值点；

④不等式 $f (m - 2) + f (m^{2}) > - 2$ 的解集是 $(- 2 ， 1)$ .

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 若a>0，b>0，且函数f(x)=4x³-ax²-2bx+2在x=1处有极值，则ab的最大值等于（）

A、2 B、3 C、6 D、9

查看试题解析
4. 在 $Δ A B C$ 中， $a ， b ， c$ 分别为 $∠ A ， ∠ B ， ∠ C$ 所对的边，若函数 $f (x) = \frac{1}{3} x^{3} + b x^{2} + (a^{2} + c^{2} - a c) x + 1$ 有极值点，则 $s i n (2 B - \frac{π}{3})$ 的最小值是

A、0 B、 $- \frac{\sqrt{3}}{2}$ C、 $\frac{\sqrt{3}}{2}$ D、-1

查看试题解析
5. 已知函数 $f (x) = a x^{2} - 2 x + \ln x$ 有两个不同的极值点 $x_{1}$ ， $x_{2}$ ，若不等式 $f (x_{1}) + f (x_{2}) < x_{1} + x_{2} + t$ 恒成立，则 $t$ 的取值范围是（）

A、 $[- 4 ， + \infty)$ B、 $[- 5 ， + \infty)$ C、 $[- 6 ， + \infty)$ D、 $[- 7 ， + \infty)$

查看试题解析
6. 已知函数 $f (x) = \cos (2 x + φ) (| φ | < \frac{π}{2})$ ， $F (x) = f (x) + \frac{\sqrt{3}}{2} f^{'} (x)$ 为奇函数，则下列叙述四个结论中正确的是（）

A、 $\tan φ = \sqrt{3}$ B、 $f (x)$ 在 $[- a ， a]$ 上存在零点，则a的最小值为 $\frac{5 π}{6}$ C、 $F (x)$ 在 $(\frac{π}{4} ， \frac{3 π}{4})$ 上单调递增 D、 $f (x)$ 在 $(0 ， \frac{π}{2})$ 有且仅有一个极大值点

查看试题解析
7. 函数 $f (x) = x^{3} + a x^{2} + b x + a^{2}$ 在 $x = 1$ 时有极值10，那么（）

A、 $a = - 3 ， b = 3$ B、 $a = 4 ， b = - 11$ C、 $a = - 3 ， b = 3$ 或 $a = 4 ， b = - 11$ D、以上均不正确

查看试题解析
8. 已知函数 $f (x) = x^{3} + a x^{2} - 3 x - 9$ 的两个极值点为 $x_{1} ， x_{2}$ ，则 $x_{1} x_{2} =$ （）

A、9 B、-9 C、1 D、-1

查看试题解析
9. 已知函数 $f (x) = \frac{1}{3} a x^{3} - x^{2} + b x$ ( $a > 0$ 且 $a \neq \frac{1}{2}$ ， $b > 0$ )的一个极值点为2，则 $\frac{1}{a} + \frac{1}{b}$ 的最小值为（）

A、 $\frac{7}{4}$ B、 $\frac{9}{4}$ C、 $\frac{8}{5}$ D、7

查看试题解析
10. 若函数 $f (x) = 2 x + \frac{1}{2} \sin 2 x - a \sin x$ 在 $(0 ， \frac{π}{2})$ 上恰有两个不同的极值点，则实数 $a$ 的取值范围是（）

A、 $(\sqrt{2} ， 3)$ B、 $(2 \sqrt{2} ， 3)$ C、 $(2 \sqrt{2} ， 4)$ D、 $(\sqrt{2} ， 6)$

查看试题解析
11. 已知函数 $f (x) = {\begin{array}{l} 3 \cdot {(\frac{1}{2})}^{x} ， x \leq 0 \\ \frac{2}{3} x^{3} - 3 x^{2} + 4 x + 3 ， x > 0 \end{array}$ ，则下列说法正确的是（）

A、函数 $f (x)$ 只有一个极值点 B、函数 $f (x)$ 的值域为 $[\frac{13}{3} ， + \infty)$ C、当 $x \in [a ， 1]$ ，且 $\log_{2} \frac{9}{13} \leq a \leq 0$ 时，函数 $f (x)$ 的取值范围是 $[3 ， \frac{14}{3}]$ D、若函数 $g (x) = {[f (x)]}^{2} - (a + 2) f (x) + 2 a$ 有4个不同的零点，则 $\frac{13}{3} < a \leq \frac{14}{3}$ .

查看试题解析

二、多选题

12. 已知函数 $f (x) = a {(x - a)}^{2} (x - b) （ a \neq 0)$ 的极大值点为 $x = a$ ，则（）

A、 $a^{2} < b^{2}$ B、 $a^{2} < a b$ C、若 $f^{'} (x_{1}) = f^{'} (x_{2}) = 0$ ，则 $x_{1} + x_{2} > 0$ D、若 $f^{'} (x_{1}) = f^{'} (x_{2}) = 0$ ，则 $x_{1} x_{2} > 0$

查看试题解析
13. 函数 $f (x) = s i n (ω x - \frac{π}{5}) (ω > 0)$ ，已知 $f (x)$ 在 $[0 ， 2 π]$ 有且仅有5个零点，下面结论正确的是（）

A、 $ω$ 的取值范围是 $[\frac{21}{10} ， \frac{13}{5})$ B、 $f (x)$ 在 $(0 ， \frac{π}{4})$ 单调递增 C、 $f (x)$ 在 $(0 ， 2 π)$ 有且仅有3个极大值点 D、 $f (x)$ 在 $(0 ， 2 π)$ 有且仅有2个极小值点

查看试题解析
14. 定义在R上的可导函数y=f(x)的导函数的图象如图所示，以下结论正确的是（）

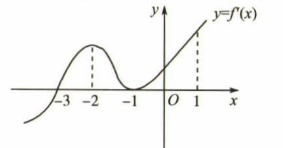A、-3是f(x)的一个极小值点 B、-2和-1都是f(x)的极大值点 C、f(x)的单调递增区间是(-3，+∞) D、f(x)的单调递减区间是(-∞，-3)

查看试题解析
15. 若函数y=f(x)的导函数的图象如图所示，则下述判断正确的是（）

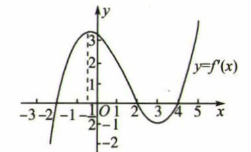A、函数y=f(x)在区间(-3，- $\frac{1}{2}$ )上单调递增 B、函数y=f(x)在区间(- $\frac{1}{2}$ ，3)上单调递减 C、函数y=f(x)在区间(4，5)内单调递增 D、当x=2时，函数y=f(x)有极大值

查看试题解析

三、填空题

16. 已知函数 $f (x) = x^{3} + 3 a x^{2} + 3 (a + 2) x + 1$ 既有极大值又有极小值，则实数 $a$ 的取值范围是.

查看试题解析
17. 已知函数 $f (x) = \frac{\ln^{2} x + 4 \ln x - 4}{x}$ ，则其极大值与极小值的和为．

查看试题解析
18. 函数 $f (x) = \frac{\cos x}{\cos 2 x}$ 的定义域为，极大值点的集合为.

查看试题解析
19. 若函数 $f (x) = x^{3} - 3 x^{2}$ 在区间 $(a - 2 ， a + 1)$ 内存在极大值，则a的取值范围是.

查看试题解析

选择性必修二 5.3 导数在研究函数中的应用 函数的极值

一、单选题

二、多选题

三、填空题

选择性必修二 5.3 导数在研究函数中的应用函数的极值