高中数学人教A版(2019)选择性必修二 5.3 导数在研究函数中的应用 函数的单调性
试卷更新日期:2022-03-20 类型:同步测试
一、单选题
-
1. 已知 , 满足 , 则( )A、 B、 C、 D、2. 设是函数的导函数,若 , 且对 , 且总有 , 则下列选项正确的是( )A、 B、 C、 D、3. 若仅存在一条直线与函数()和的图象均相切,则实数( )A、e B、 C、2e D、4. 已知函数 , 若不等式在区间上恒成立,则实数的取值范围为( )A、 B、 C、 D、5. 函数的单调递减区间为( )A、 B、 C、 D、6. 已知函数(m>0)的单调递减区间为 , 若 , 则m的最大值为( )A、1 B、2 C、3 D、67. 已知函数是定义在上的奇函数,是的导函数,且 , 当时 , 则使得成立的的取值范围是( )A、 B、 C、 D、8. 已知函数 ,若关于 的不等式 恒成立,则实数 的取值范围为( )A、 B、 C、 D、9. 已知定义在上的函数满足 , 且有 , 则的解集为( )A、 B、 C、 D、10. 函数fx)的导函数f'(x)的图象如图所示,那么f(x)的图象最有可能是( )
 A、
A、 B、
B、 C、
C、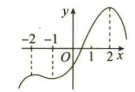 D、
D、 11. 若函数f(x)=x2- lnx+1在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围为( )A、[1,+∞) B、[1. ) C、[1,2) D、[ ,2)12. 若函数f(x)=2x3+ax2+1(a为常数)在区间(-∞,0)和(2,+∞)上单调递增,且在区间(0,2)上单调递减,则a的值为( )A、1 B、2 C、-6 D、-12
11. 若函数f(x)=x2- lnx+1在其定义域内的一个子区间(k-1,k+1)内不是单调函数,则实数k的取值范围为( )A、[1,+∞) B、[1. ) C、[1,2) D、[ ,2)12. 若函数f(x)=2x3+ax2+1(a为常数)在区间(-∞,0)和(2,+∞)上单调递增,且在区间(0,2)上单调递减,则a的值为( )A、1 B、2 C、-6 D、-12二、填空题
-
13. 若函数 在 上有两个不同的零点,则实数 的取值范围为.14. 已知函数在上是单调递增函数,则实数的取值范围是.15. 已知函数f(x)=x3-3ax2-bx,其中 a ,b为实数.若f(x)在区间[-1,2]上为减函数,且b=9a,则a的取值范围是.16. 函数f(x)=1+x+cosx在上的单调递增区间是.
三、解答题