浙教版初中数学八下第五章特殊平行四边形优生加练

试卷更新日期：2022-03-19 类型：复习试卷

进入出卷网下载

一、综合题

1. （一）问题情境：如图1，已知点E，F分别在正方形 $A B C D$ 的边 $A B$ ， $B C$ 上，且 $B E = B F$ ，点M为 $A F$ 的中点，连接 $C E$ ， $B M$ .

(1)、线段 $C E$ 与 $B M$ 之间的数量关系是，位置关系是.

(2)、（二）猜想证明：
如图2，将线段 $B E$ 和 $B F$ 绕点B逆时针旋转，旋转角均为 $α$ （ $0 ° < α < 90 °$ ）.点M为线段 $A F$ 的中点，连接 $B M$ ，请你判断（1）中的两个结论是否仍然成立.若成立，请证明；若不成立，请说明理由.

(3)、（三）探索发现：
将图1中的线段 $B E$ 和 $B F$ 绕点B逆时针旋转，旋转角为 $α = 90 °$ ，点M为线段 $A F$ 的中点，得到如图3所示的图形，请你判断线段 $C E$ 与 $B M$ 之间的数量关系是否发生变化，请说明理由.

查看试题解析
2. 如图，已知四边形ABCD是正方形，点E是AD边上的一点（不与点A，D重合），连接CE，以CE为一边作正方形CEFG，使点F，G与点A，B在CE的两侧，连接BE并延长，交GD延长线于点H．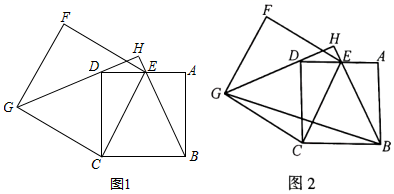
　

(1)、如图1，请判断线段BE与GD的数量关系和位置关系，并说明理由；

(2)、如图2，连接BG，若AB＝2，CE＝ $\sqrt{5}$ ，请你直接写出 $\sqrt{D E^{2} + B G^{2}}$ 的值．

查看试题解析
3. 如图， $B D$ 是正方形 $A B C D$ 的对角线， $B C = 2$ .边 $B C$ 在其所在的直线上平移，将通过平移得到的线段记为 $P Q$ ，连接 $P A$ 、 $Q D$ ，并过点 $Q$ 作 $Q O ⊥ B D$ ，垂足为 $O$ ，连接 $O A$ 、 $O P$ .

(1)、请直接写出线段 $B C$ 在平移过程中，四边形 $A P Q D$ 是什么四边形；

(2)、请判断 $O A$ 、 $O P$ 之间的数量关系和位置关系，并加以证明；

(3)、在平移变换过程中，设 $y = S_{Δ O P B}$ ， $B P = x (0 \leq x \leq 2)$ ，求 $y$ 与 $x$ 之间的函数关系式.

查看试题解析
4. 如图1所示将一块等腰三角板BMN放置与正方形ABCD的∠B重合，连接AN、CM，E是AN的中点，连接BE.

(1)、（观察猜想）
CM与BE的位置关系是；CM与BE的数量关系是；

(2)、（探究证明）
如图2所示，把三角板BMN绕点B逆时针旋转a（0<a<90），其他条件不变，线段CM与BE的关系是否仍然成立，并说明理由：

(3)、（拓展延伸）
若旋转角a=45°，且∠NBE=2∠ABE，求 $\frac{BC}{BN}$ 的值.

查看试题解析
5. 如图，菱形ABCD的对角线AC，BD相交于点O，过点D作DE//AC且DE=OC，连结CE.

(1)、求证：四边形OCED是矩形.

(2)、连结AE交OD于点F，若菱形ABCD的边长为6，∠ABC=60°，求AE的长.

查看试题解析
6. 如图，已知矩形ABCD，连接AC，EF垂直平分AC于点O，分别交AD、BC于点E、点F，连接FC.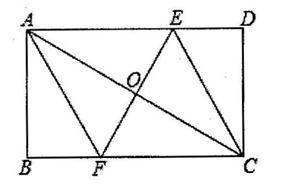

(1)、求证：四边形AECF是菱形；

(2)、若△CEF与△CED的面积比为3∶1，且AB=4，求四边形AECF的面积.

查看试题解析
7. （问题发现）数学小组成员小明做作业时遇到以下问题：

图1 图2 图3

(1)、若四边形 $A B C D$ 是菱形， $∠ A B C = 60 °$ ，点 $P$ 是射线 $B D$ 上一动点，以 $A P$ 为边向右侧作等边 $△ A P E$ ，如图1，当点E在菱形 $A B C D$ 内部或边上时，连接 $C E 、 C A$ ，则 $B P$ 与 $C E$ 有怎样的数量关系？请直接写出你的猜想；

(2)、（类比探究）数学小组对该问题进行进一步探究：
若四边形 $A B C D$ 是正方形，点P是射线 $B D$ 上一动点，以 $A P$ 为直角边在 $A P$ 边的右侧作等腰 $R t △ A P E$ ，其中 $∠ A P E = 90 ° ， A P = P E$ .

①如图2，当点 $P$ 在对角线 $B D$ 上时，小组发现点 $E$ 恰好在射线 $C D$ 上，求 $B P$ 与 $C E$ 之间的数量关系（过程只用说明点 $E$ 在线段 $C D$ 上的情况即可）；

②如图3，当P是对角线 $B D$ 的延长线上一动点时，小组发现点 $E$ 恰好在射线 $C D$ 上，连接 $B E$ ，若 $B E = 6 ， A B = 2$ ，求 $△ B P E$ 的面积．

查看试题解析
8. 【概念学习】若两个等腰三角形有公共底边，则称这两个等腰三角形的顶角的顶点关于这条公共底边互为顶针点，这条公共底边叫做这两个互为顶针点的顶针线段，如图（1），四边形ABCD ，BC是一条对角线，AB=AC，DB=DC，则点A与点D关于顶针线段BC互为顶针点.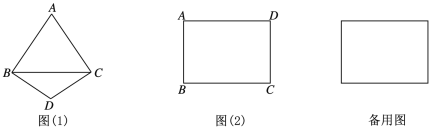

(1)、【实践操作】如图（2），在长方形ABCD中，AB<AD.若在AD边上存在点F，边AB 上存在点E，使得点E与点C关于顶针线段BF互为顶针点，请用直尺和圆规在图2中作出满足条件的点F、E.(要求不写作法，保留作图痕迹.

(2)、【思维探究】在上述的条件下，若AB=8，AD=10.请利用备用图求AE的长度.

查看试题解析
9. 如图，O为原点，长方形 $O A B C$ 与 $O D E F$ 的面积都为12，且能够完全重合，边 $O A$ 在数轴上， $O A = 3$ ．长方形 $O D E F$ 可以沿数轴水平移动，移动后的长方形 $O D E F$ 与 $O A B C$ 重叠部分的面积记为S．

(1)、如图1，求出数轴上点F表示的数．

(2)、当S恰好等于长方形 $O A B C$ 面积的一半时，求出数轴上点 $O$ 表示的数．

(3)、在移动过程中，设P为线段 $O^{^{'}} A$ 的中点，点 $F ， P$ 所表示的数能否互为相反数？若能，求点O移动的距离；若不能，请说明理由．

查看试题解析
10. 如图，在长方形 $A B C D$ 中， $A B = 4$ ， $B C = 6$ ．延长 $B C$ 到点 $E$ ，使 $C E = 3$ ，连接 $D E$ ．动点 $P$ 从点 $B$ 出发，沿着 $B E$ 以每秒1个单位的速度向终点 $E$ 运动，点 $P$ 运动的时间为 $t$ 秒．

(1)、 $D E$ 的长为；

(2)、连接 $A P$ ，求当 $t$ 为何值时， $△ A B P ≅ △ D C E$ ；

(3)、连接 $D P$ ，求当 $t$ 为何值时， $△ P D E$ 是直角三角形；

(4)、直接写出当 $t$ 为何值时， $△ P D E$ 是等腰三角形．

查看试题解析
11. 如图，在长方形ABCD中，AB＝CD＝6cm，BC＝10cm，点P从点B出发，以2cm/秒的速度沿BC向点C运动，设点P的运动时间为t秒：

(1)、PC＝cm.（用t的代数式表示）

(2)、当t为何值时，△ABP≌△DCP？

(3)、当点P从点B开始运动，同时，点Q从点C出发，以vcm/秒的速度沿CD向点D运动，是否存在这样v的值，使得△ABP与△PQC全等？若存在，请求出v的值；若不存在，请说明理由.

查看试题解析
12. 如图，在矩形ABCD中，AB=6 ， BC=8 ，将矩形ABCD绕点D按顺时针方向旋转，得到矩形EFGD ，直线DE ， FG分别与直线BC交于点P ， Q.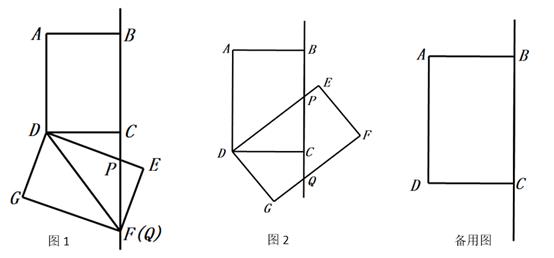

(1)、如图1，当矩形EFGD的顶点F落在线段BC的延长线上时，求DP的长．

(2)、如图2，在矩形旋转过程中，当P位于线段BC上时，求证：DP=PQ.

(3)、在旋转过程中，旋转角 $α$ 满足 $0^{\circ} < α \leq 90^{\circ}$ ，当 $B P = \frac{1}{2} B Q$ 时，求CP的长（直接写出答案）.

查看试题解析
13. 如图，C为线段BD上一动点，分别过点B，D作AB⊥BD，DE⊥BD，连结AC，CE.

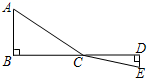(1)、已知AB=3，DE=2，BD=12，设CD=x.用含x的代数式表示AC+CE的长；

(2)、请问点C满足什么条件时，AC+CE的值最小？并求出它的最小值；

(3)、根据（2）中的规律和结论，请构图求出代数式 $\sqrt{x^{2} + 4} + \sqrt{{(8 - x)}^{2} + 16}$ 的最小值.

查看试题解析
14. 如图1，在平面直角坐标系xOy中，直线AB：y＝kx+b（b≠0）分别与y轴，x轴交于A，B两点，点E，点G分别为AB，OE中点，点A，B关于点G的对称点分别为C，D，则称四边形ABCD为直线AB的伴随四边形，直线CD为直线AB的伴随直线.

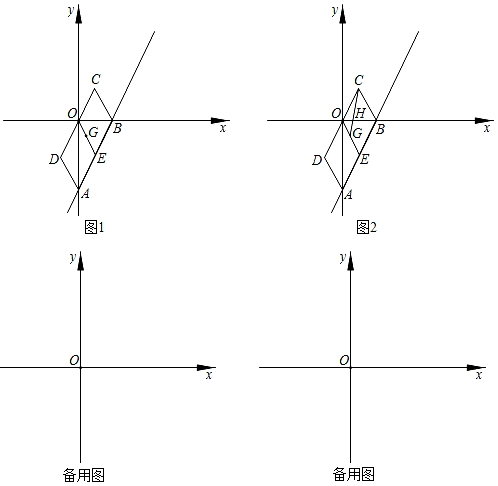(1)、若伴随四边形为矩形，则k＝；

(2)、已知伴随直线为y＝﹣4x，四边形ABCD的面积为25，求直线AB的解析式；

(3)、如图2，连结CG，与x轴交于点H，若△BHC为等腰三角形且k＞0，求k的值.

查看试题解析
15. 如图，在Rt△ABC中，∠C＝90°，∠ABC＝30°，D，E是斜边AB上的两个动点（不与点A，B重合），过E作EF⊥BC于点F，设BD＝m，EF＝n，且m＝12﹣4n，连结DF.

(1)、当m＝8时，
①求DE长；

②求△BDF的面积.

(2)、是否存在点P，使得以D，E，F，P四点为顶点的四边形是菱形，若存在，请求出n的值，若不存在，请说明理由；

(3)、当点B关于直线DF的对称点B'落在直线EF上时，请直接写出n的值.

查看试题解析
16. 如图，在菱形ABCD中，CE⊥AB于点E.

(1)、若CE＝4，AE＝2BE，求菱形ABCD的周长；

(2)、连结BD交CE于点F；
①若DF＝BF＋2EF，求证：AE＝BE.

②设四边形AEFD和△CDF的面积分别是S₁和S₂ ，若AE＝4，S₁﹣S₂＝2 $\sqrt{2}$ ，求线段BF的长.

查看试题解析
17. 如图，在菱形ABCD中，∠BAD=120°，线段AE与AB重合，以AE为边向右侧作正三角形AEF，△AEF绕点A按逆时针方向旋转，旋转角∠BAE=α(0°<α<60°)，射线BE，DF交于点G，连结CE，CG，CF。

(1)、求证：BE=CF；

(2)、求∠BGD的度数；

(3)、当△ECG为等腰三角形时，求 $\frac{B E}{F G}$ 的值。

查看试题解析
18. 如图，E、F、G、H分别是菱形ABCD四边上的点，且AH＝AE＝CF＝CG，连结EF、FG、GH、HE.

(1)、求证：四边形EFGH是矩形；

(2)、若∠D＝120°，S_矩形EFGH＝ $\frac{1}{3}$ S_菱形ABCD ，求 $\frac{D G}{G C}$ 的值.

查看试题解析
19. 如图，在正方形ABCD中，E是对角线AC上一点，FH⊥AC于点E，交AD，AB于点F，H.

(1)、求证：CF＝CH；

(2)、若AH＝ $\frac{1}{3}$ CH，AB＝4，求AH的长.

查看试题解析
20. 如图1，四边形ABCO为正方形，若点A坐标为（0，5）

(1)、如图1，直接写出点B的坐标

(2)、如图1，点D为线段OA上一点，连接BD，若点A到BD的距离为1，求点C到BD的距离.

(3)、如图2，若D为x轴上一点，且OD=2，M为y轴正半轴上一点，且∠DBM=45°，直接写出点M的坐标

查看试题解析
21. 如图

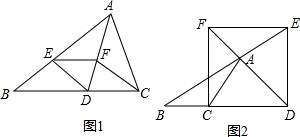(1)、如图1，△ABC中，AB＞AC，AD平分∠BAC交BC于点D，在AB上截取AE＝AC，过点E作EF∥BC交AD于点F.求证：①△ADE≌△ADC；②四边形CDEF是菱形；

(2)、如图2，△ABC中，AB＞AC，AD平分△ABC的外角∠EAC交BC的延长线于点D，在AB的反向延长线上截取AE＝AC，过点E作EF∥BC交AD的反向延长线于点F.四边形CDEF还是菱形吗？如果是，请给出证明；如果不是，请说明理由；

(3)、在（2）的条件下，四边形CDEF能是正方形吗？如果能，直接写出此时△ABC中∠BAC与∠B的关系；如果不能，请直接回答问题，不必说明理由.

查看试题解析
22. 如图，在正方形ABCD中，P是边BC上的一动点(不与点B，C重合)，点B关于直线AP的对称点为E，连接AE.连接DE并延长交射线AP于点F，连接BF，CF.

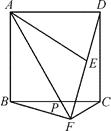(1)、若∠BAP＝α，直接写出∠ADF的大小(用含α的式子表示).

(2)、求证：BF⊥DF.

(3)、求证：AF 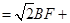CF.

查看试题解析

浙教版初中数学八下第五章 特殊平行四边形优生加练

一、综合题

浙教版初中数学八下第五章特殊平行四边形优生加练