陕西省咸阳市泾阳县2021-2022学年九年级下学期教学衔接质量检测数学试卷
试卷更新日期：2022-03-18 类型：月考试卷
一、选择题（共8小题，每小题3分，计24分每小题只有-个选项是符合题意的）
-
1. 计算sin 45°+cos45°的值为（ ）A、1 B、2 C、 D、22. 如图所示的几何体的左视图是（ ）
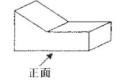A、
B、
C、
D、
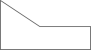3. 如图，五边形ABCDE是由五边形FGHMN经过位似变换得到的，点O是位似中心，F、G、H、M、N分别是OA、OB、OC、OD、OE的中点，则五边形ABCDE与五边形FGHMN的面积比是（ ）
A、2：1 B、4：1 C、5：1 D、6：14. 已知正比例函数y=kx与反比例函数y= 的图象交于A、B两点，若点A（m，4），则点B的坐标为（ ）A、（1，-4） B、（-1，4） C、（4，-1） D、（-4，1）5. 在一个不透明的盒子中有20个除颜色外均相同的小球，每次摸球前先将盒中的球摇匀，随机摸出一个球记下颜色后再放回盒中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.5，由此可估计袋中红球的个数为（ ）A、12个 B、10个 C、8个 D、6个6. 若关于x的一元二次方程x2+6x+c=0有实数根，则c应满足的条件是（ ）A、c>9 B、c≥9 C、c<9 D、c≤97. 如图，在矩形 中， 分别是 的中点， ，则 的长为（ ）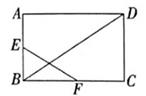
A、6 B、5 C、4 D、38. 当0≤x≤m时，函数y=-x2+4x-3的最小值为-3，最大值为1，则m的取值范围是（ ）A、-1≤m≤0 B、2≤m< C、2≤m≤4 D、 <m≤9. 若cosα=0.5，则锐角α为度．10. 如图，已知路灯离地面的高度AB为4.8m，身高为1.6 m的小明站在D处的影长DC为2 m，那么此时小明离路灯杆AB的距离BD为m
11. 疫情期间，某快递公司推出无接触配送服务，第一周的订单数是5万件，第三周的订单数为7.2万件，如果设平均每周订单数的增长率为x，根据题意列方程为12. 如图，在直角坐标系中，点A、B是反比例函数y= 图象上的两点，过A作AM⊥x轴，过B作BN⊥y轴，则图中阴影部分的面积为
13. 如图，正方形ABCD和正方形AEFG的边长分别为5 cm和3 cm，点E、G分别为AB、AD边上的点，H为CF的中点，连接HG，则HG的长为cm．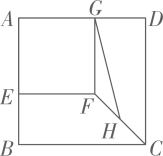
二、解答题（共13小题，计81分解答应写出过程）
-
14. 解方程：2（x+5）=3x（x+5）．15. 已知二次函数的表达式为y= x2+x+2．(1)、求该二次函数图象的开口方向、对称轴和顶点坐标；(2)、当x小于多少时，y随x的增大而增大？16. 如图，在△ABC中，∠C=90°，AB=10，sinB= 。求BC的长及∠A的正切值．
17. 已知反比例函数y= 的图象经过第二、四象限，求n的取值范围．18. 如图，在△ABC和OACD中，AD⊥CD于点D，AC⊥BC于点C．请再添加一个条件，使△ABC∽△CAD，并加以证明．
19. 某气球内充满了一定质量的气体，当温度不变时，气球内气体的气压p（kPa）是气体体积V（m）的反比例函数，其图象如图所示．
(1)、求这个函数的表达式；(2)、当气球的体积是1m3时，气球内的气压是多少千帕？20. 如图，AB表示一个窗户的高，AM和BN表示射人室内的光线，窗户的下端到地面的距离BC=1m．已知某一时刻BC在地面的影长CN=1.5m，AC在地面的影长CM=4.5m，求窗户的高度AB．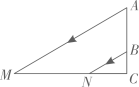
21. 如图，点E在菱形ABCD的边BC的延长线上，AE交CD于点F，FG∥CE交DE于点G．求证：FG=FC．
22. 某校举行歌唱比赛，歌曲有：《没有共产党就没有新中国》，《歌唱祖国》，《少年中国说》（分别用字母A，B，C依次表示这三首歌曲）．比赛时，将A，B，C这三个字母分别写在3张无差别不透明的卡片正面上，洗匀后正面向下放在桌面上，九（1）班班长先从中随机抽取一张卡片，放回后洗匀，再由九（2）班班长从中随机抽取一张卡片，进行歌唱比赛，(1)、九（1）班抽到歌曲《少年中国说》的概率是(2)、试用画树状图或列表的方法表示所有可能的结果，并求出九（1）班和九（2）班抽到不同歌曲的概率．23. 如图，在四边形ABCD中，对角线AC与BD相交于点E，且∠CAB=∠CBD，已知AB=4，AC=6，BC=5，BD=5.5．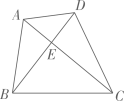
(1)、求DE的长；(2)、求 的值．24. 2022年杭州亚运会，即第19届亚洲运动会，将于2022年9月10日至25日，在中国杭州市举行某网络经销商购进了一批以亚运会为主题，且具有中国风范、杭州韵味的文化衫进行销售．文化衫的进价为每件30元，当销售单价定为70元时，每天可售出20件．为了扩大销售，增加盈利，决定采取适当的降价措施，经调查发现：销售单价每降低1元，则每天可多售出2件（销售单价不低于进价），若设这款文化衫的销售单价为x（元），销售这款文化衫每天所获得的利润为w（元）．(1)、求每天所获得的利润w（元）与销售单价x（元）之间的函数关系式；(2)、当销售单价定为多少元时，销售这款文化衫每天所获得的利润最大？并求出最大利润。25. 某一天，小明和小亮想利用所学过的测量知识来测量G棵古树的高度AB．他们带着测量工具来到这棵古树前，由于有围栏保护，他们无法到达古树的底部B，如图所示，于是他们先在古树周围的空地上选择一点D，通过测倾器测得树的顶端A的仰角为45°，再在BD的延长线上确定一点F，使DF=5米，并在F处通过测倾器测得树的顶端A的仰角为30°，测倾器的高度CD=EF=1米已知点FD、B在同一水平直线上，且EF、CD、AB均垂直于FB，则这棵古树的高度AB为多少米？（结果保留根号）
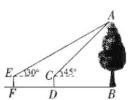26. 如图，二次函数y=ax2+bx-3的图象与x轴交于A（-3，0），B（1，0）两点，与y轴交于点C．
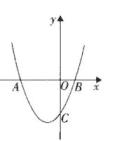(1)、求该二次函数的表达式；(2)、若点D在x轴的上方，以A、B、D为顶点的三角形与△ABC全等，平移该二次函数图象，使平移后的图象经过点B与点D，请你写出平移过程，并说明理由．