苏科版初中数学七年级下册 9.4 乘法公式同步训练（基础版）

试卷更新日期：2022-03-18 类型：同步测试

进入出卷网下载

一、单选题

1. 下列等式中，成立的是（）

A、 $(x + y)^{2} = x^{2} + y^{2}$ B、 $(x - y)^{2} = x^{2} - y^{2}$ C、 ${(x - y)}^{2} = x^{2} - 2 x y + y^{2}$ D、 $(- x + y) (x - y) = x^{2} - y^{2}$

查看试题解析
2. 下列各式中运算结果是 $9 a^{2} - 25 b^{2}$ 的是（）．

A、 $(- 5 b + 3 a) (- 5 b - 3 a)$ B、 $(5 b - 3 a) (- 5 b - 3 a)$ C、 $(5 b + 3 a) (5 b - 3 a)$ D、 $(5 b + 3 a) (- 5 b - 3 a)$

查看试题解析
3. 下列各式能用平方差公式计算的是 $($ 　　 $)$

A、 $(2 a + b) (2 b - a)$ B、 $(- \frac{1}{2} x + 1) (- \frac{1}{2} x - 1)$ C、 $(a + b) (a - 2 b)$ D、 $(2 x - 1) (- 2 x + 1)$

查看试题解析
4. 若 $a + b = - 4$ ， $a b = 3$ ，则 $a^{2} + b^{2} =$ （）

A、5 B、10 C、13 D、22

查看试题解析
5. 多项式x²+A+1是个完全平方式，那么代数式A不可能为（）

A、2x B、x C、﹣2x D、 $\frac{1}{4}$ x⁴

查看试题解析
6. 下列乘法公式的运用，错误的是（）

A、 $(2 x - 3) (2 x + 3) = 4 x^{2} - 9$ B、 ${(- 4 x - 1)}^{2} = 16 x^{2} - 8 x + 1$ C、 ${(3 - 2 a)}^{2} = 4 a^{2} + 9 - 12 a$ D、 $(- 2 x + 3 y) (3 y + 2 x) = 9 y^{2} - 4 x^{2}$

查看试题解析
7. 如图在边长为a的正方形中挖掉一个边长为b的小正方形(a＞b)．把余下的部分剪拼成一个长方形，通过计算阴影部分的面积，验证了一个等式，则这个等式是（）

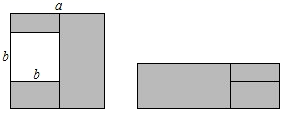A、a²﹣2ab+b²＝(a﹣b)² B、a²﹣ab＝a(a﹣b) C、a²﹣b²＝(a﹣b)² D、a²﹣b²＝(a+b)(a﹣b)

查看试题解析
8. 若（2021²﹣4）（2020²﹣4）＝2023×2019×2018m ，则m的值是（）

A、2020 B、2021 C、2022 D、2024

查看试题解析
9. 已知 $M = 2022^{2} ， N = 2021 \times 2023$ ，则 $M$ 与 $N$ 的大小关系是（）

A、 $M > N$ B、 $M < N$ C、 $M = N$ D、不能确定

查看试题解析
10. 对于任何实数m、n，多项式m²+n²-6m-10n+36的值总是（）

A、非负数 B、0 C、大于2 D、不小于2

查看试题解析

二、填空题

11. 计算 $(a - 2) (a + 2) =$ ．

查看试题解析
12. 计算 ${(a - 3)}^{2}$ 的结果为

查看试题解析
13. 一个正方形的面积为 $x^{2} + 4 x + 4 (x > 0)$ ，则它的边长为

查看试题解析
14. 已知 $4 m^{2} - 9 n^{2} = 26 ， 2 m + 3 n = 13$ ，则 $2 m - 3 n =$ .

查看试题解析
15. 若（a+b）²=9，（a-b）²=4，则a²+b²=.

查看试题解析
16. 已知 $a - \frac{1}{a} = 5$ ，则 $a^{2} + \frac{1}{a^{2}}$ 的值是．

查看试题解析
17. 若 $a + b = 4 ， a - b = 1$ ，则 ${(a + 1)}^{2} - {(b - 1)}^{2}$ 的值为.

查看试题解析
18. 如果（a+b+1）（a+b-1）=3，那么a+b的值为.

查看试题解析

三、解答题

19. 计算： $(x + 5) (x - 5) + (x - 3) (3 - x)$ ．

查看试题解析
20. 已知3x²＋2x﹣5＝0，求代数式（2x＋1）（2x﹣1）﹣x（x﹣2）的值．

查看试题解析
21. 计算： $（ x - 3 y + 2 c) (x + 3 y + 2 c)$ ．

查看试题解析
22. 当n为自然数时，(n+7)²-(n-5)²能被24整除吗？说明理由．

查看试题解析
23.

(1)、已知a+b＝1，ab＝﹣3，求a²﹣3ab+b²的值.

(2)、已知a﹣ $\frac{1}{a}$ ＝2，求a²+ $\frac{1}{a^{2}}$ 和a⁴+ $\frac{1}{a^{4}}$ 的值.

查看试题解析
24. 阅读材料：若x²－2xy＋2y²－8y＋16=0，求x、y的值.
解：∵x²－2xy＋2y²－8y＋16=0，∴(x²－2xy＋y²)＋(y²－8y＋16)=0，∴(x－y)²＋(y－4)²=0，∴(x－y)²=0，(y－4)²=0，∴y=4，x=4.

根据你的观察，探究下面的问题：

已知△ABC的三边长a、b、c都是正整数，且满足a²＋b²－4a－6b＋13=0.求△ABC的边c的值.

查看试题解析
25. 观察下列等式：
（x﹣1）（x+1）=x²﹣1
（x﹣1）（x²+x+1）=x³﹣1
（x﹣1）（x³+x²+x+1）=x⁴﹣1
（x﹣1）（x⁴+x³+x²+x+1）=x⁵﹣1…
运用上述规律，试求2⁶+2⁵+2⁴+2³+2²+2+1的值．

查看试题解析
26.

(1)、在下列横线上用含有a，b的代数式表示相应图形的面积.

①a²；②. ③b² ； ④.

(2)、请在图④画出拼图并通过拼图，你发现前三个图形的面积与第四个图形面积之间有什么关系？请用数学式子表达：.

(3)、利用（2）的结论计算10.23²+20.46×9.77+9.77²的值.

查看试题解析

苏科版初中数学七年级下册 9.4 乘法公式 同步训练（基础版）

一、单选题

二、填空题

三、解答题

苏科版初中数学七年级下册 9.4 乘法公式同步训练（基础版）