广西岑溪市2020-2021学年高一下学期数学期中考试试题试卷

试卷更新日期：2022-03-18 类型：期中考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x ∣ - 1 < x < 3}$ ， $B = {- 1 ， 1 ， 2}$ ，则 $A ∩ B =$ （）

A、 ${1 ， 2}$ B、 ${- 1 ， 1 ， 2}$ C、 ${0 ， 1 ， 2}$ D、 ${- 1 ， 0 ， 1 ， 2 ， 3}$

查看试题解析
2. 已知角 $α$ 的终边在第三象限，则点 $P (t a n α ， c o s α)$ 在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 一个人打靶时连续射击两次，事件“两次都没中靶”的相互对立事件是（）

A、至多有一次中靶 B、至少有一次中靶 C、两次都中靶 D、只有一次中靶

查看试题解析
4. “瓦当”是中国古建筑装饰檐头的附件，是中国特有的文化艺术遗产，为探究下面“瓦当”图案的面积，向半径为10的圆内投入1000粒芝麻，落入阴影部分的有400粒.则估计“瓦当”图案的面积是（）

A、40 B、40π C、4 D、4π

查看试题解析
5. 已知函数 $f (x) = 3^{x} - {(\frac{1}{3})}^{x}$ ，则 $f (x)$ （）

A、是奇函数，且在 $(- \infty ， + \infty)$ 上是减函数 B、是偶函数，且在 $(- \infty ， + \infty)$ 上是减函数 C、是奇函数，且在 $(- \infty ， + \infty)$ 上是增函数 D、是偶函数，且在 $(- \infty ， + \infty)$ 上是增函数

查看试题解析
6. 已知扇形AOB的周长为8，面积为4，则扇形AOB的半径是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 执行如图所示的程序框图，如果输入的 $m$ ， $n$ 分别为32，24，则输出的 $m$ 值是（）

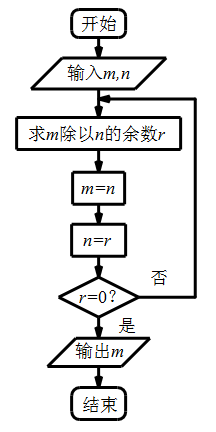A、0 B、4 C、8 D、12

查看试题解析
8. 设三棱柱的侧棱垂直于底面，所有棱长都为 $a$ ，顶点都在一个球面上，则该球的表面积为（）

A、 $π a^{2}$ B、 $\frac{7}{3} π a^{2}$ C、 $\frac{11}{3} π a^{2}$ D、 $5 π a^{2}$

查看试题解析
9. 已知直线 $k x - y + k + 1 = 0$ 过定点 $A$ ，则点 $A$ 关于 $x + y - 3 = 0$ 对称点的坐标为（）

A、 $(2 ， 4)$ B、 $(4 ， 2)$ C、 $(2 ， 2)$ D、 $(4 ， 4)$

查看试题解析
10. 某校举行演讲比赛，9位评委给选手 $A$ 打出的分数如茎叶图所示，统计员在去掉一个最高分和一个最低分后，算得平均分为91，复核员在复核时，发现有一个数字(茎叶图中的 $x$ )无法看清，若统计员计算无误，则数字 $x$ 应该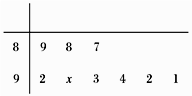是（）

A、5 B、4 C、3 D、2

查看试题解析
11. 设a=log₃2，b=log₅3，c= $\frac{2}{3}$ ，则（）

A、a<c<b B、a<b<c C、b<c<a D、c<a<b

查看试题解析
12. 已知⊙M： $x^{2} + y^{2} - 2 x - 2 y - 2 = 0$ ，直线 $l$ ： $2 x + y + 2 = 0$ ，P为l上的动点，过点P作⊙M的切线 $P A, P B$ ，切点为 $A, B$ ，当 $| P M | \cdot | A B |$ 最小时，直线 $A B$ 的方程为（）

A、 $2 x - y - 1 = 0$ B、 $2 x + y - 1 = 0$ C、 $2 x - y + 1 = 0$ D、 $2 x + y + 1 = 0$

查看试题解析

二、填空题

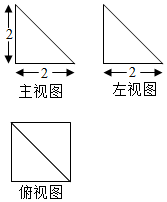
13. 某校高二（1）班共有48人，学号依次为1，2，3， $⋯$ ， 48，现用系统抽样的方法等距离抽取一个容量为6的样本．已知学号为3，11，19，35，43的同学在样本中，那么还有一名同学的学号为．

查看试题解析
14. 某四棱锥的三视图如图所示，则此四棱锥最长的棱长为．

查看试题解析
15. 直线 $l ： y = x + b$ 与曲线 $C ： y = \sqrt{1 - x^{2}}$ 有两个公共点，则 $b$ 的取值范围是.

查看试题解析
16. 已知函数 $f (x)$ 的定义域为R，图象恒过（0，1）点，对任意的 $x_{1} ， x_{2} \in R$ 当 $x_{1} \neq x_{2}$ 时，都有 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} > 1$ ，则不等式 $f [l n (e^{x} - 1)] < 1 + l n (e^{x} - 1)$ 的解集为．

查看试题解析

三、解答题

17. 设圆的方程为 $x^{2} + y^{2} - 4 x - 5 = 0$

(1)、求该圆的圆心坐标及半径.

(2)、若此圆的一条弦AB的中点为 $P (3, 1)$ ，求直线AB的方程.

查看试题解析
18. 如图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC，E是PC的中点．

(1)、证明：PA//平面EDB；

(2)、证明：DE⊥平面PBC．

查看试题解析
19. 如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 $x$ （吨）与相应的生产能耗 $y$ （吨）标准煤的几组对照数据：
$x$
3
4
5
6
$y$
2.5
3
4
4.5
（参考：用最小二乘法求线性回归方程系数公式 $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \cdot \bar{y}}{\sum_{i = 1}^{n} {x_{i}}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ）

(1)、请根据表中提供的数据，用最小二乘法求出 $y$ 关于 $x$ 的线性回归方程 $\hat{y} = \hat{b} x + \hat{a}$ ；

(2)、已知该厂技术改造前100吨甲产品能耗为90吨标准煤，试根据（1）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤？

查看试题解析
20. 如图①，圆O的直径AB＝2，圆上两点C，D在直线AB的两侧，且∠CAB＝45°；∠DAB＝60°，沿直线AB将半圆ACB折起，使两个半圆所在的平面互相垂直（如图②）．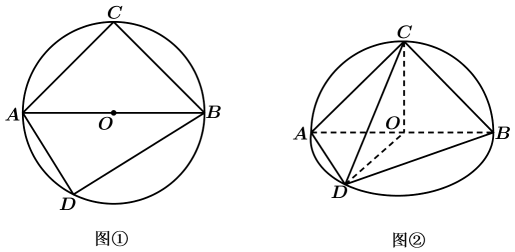

(1)、求三棱锥O－BCD的体积；

(2)、求直线CD与平面ABC所成角的正切值．

查看试题解析
21. 世界各国越来越关注环境保护问题，某检测点连续100天监视空气质量指数（AQI），将这100天的AQI数据分为五组，各组对应的区间为 $[0 ， 50) ， [50 ， 100) ， [100 ， 150) ， [150 ， 200) ， [200 ， 250]$ .并绘制出如图所示的不完整的频率分布直方图.

(1)、请将频率分布直方图补充完整；

(2)、已知空气质量指数AQI在 $[0 ， 50)$ 内的空气质量等级为优，在 $[50 ， 100)$ 内的空气质量等级为良，分别求这100天中空气质量等级为优与空气质量等级为良的天数；

(3)、在（2）的条件下，在空气质量等级为优和良的天数中，先按分层抽样的方法已经选定了6天，然后再从这6天中任取两天，求这两天的空气质量等级相同的概率.

查看试题解析
22. 已知函数f（x）=x²﹣3mx+n（m＞0）的两个零点分别为1和2．

(1)、求m、n的值；

(2)、若不等式f（x）﹣k＞0在x∈[0，5]恒成立，求k的取值范围．

(3)、令 $g (x) = \frac{f (x)}{x}$ ，若函数F（x）=g（2^x）﹣r2^x在x∈[﹣1，1]上有零点，求实数r的取值范围．

查看试题解析

$x$	3	4	5	6
$y$	2.5	3	4	4.5