2021-2022学年浙教版数学七下第五章分式单元检测卷

试卷更新日期：2022-03-18 类型：单元试卷

进入出卷网下载

一、单选题(共10题，共30分）

1. 在代数式 $\frac{3}{a}$ ， $\frac{2 x - 3 y}{4}$ ， $\frac{1}{2} (m - n)$ ， $\frac{x - y}{x + y}$ ， $\frac{1}{π}$ 中属于分式的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 下列各式从左到右的变形，正确的是（　　）

A、 $\frac{- a + b}{a - b}$ ＝﹣1 B、 $\frac{b}{a} = \frac{b^{2}}{a^{2}}$ C、 $\frac{0.1 a - 0.3 b}{0.2 a + b} = \frac{a - 3 b}{2 a + b}$ D、 $\frac{- a - b}{- a + b} = \frac{a - b}{a + b}$

查看试题解析
3. 某工厂生产空气净化器，实际平均每天比原计划多生产100台空气净化器，实际生产1200台空气净化器的时间与原计划生产900台空气净化器所需时间相同．若设原计划每天生产 $x$ 台空气净化器，则根据题意可列方程为（）

A、 $\frac{1200}{x + 100} = \frac{900}{x}$ B、 $\frac{1200}{x - 100} - \frac{900}{x} = 0$ C、 $\frac{900}{x + 100} = \frac{1200}{x}$ D、 $\frac{1200}{x} - \frac{900}{x} = 100$

查看试题解析
4. 若分式 $\frac{x^{2}}{x － 2 y}$ 中的x和y都扩大2倍，那么分式的值（）

A、扩大2倍 B、不变 C、缩小2倍 D、扩大4倍

查看试题解析
5. ${(\frac{a - b}{b})}^{2} \times \frac{b}{a^{2} - b^{2}}$ 的结果是（）

A、 $\frac{1}{b}$ B、 $\frac{a - b}{a b + b^{2}}$ C、 $\frac{a - b}{a + b}$ D、 $\frac{1}{b (a + b)}$

查看试题解析
6. 下列等式正确的是（）

A、 $| - 3 | + \tan 45 ° = - 2$ B、 ${(x y)}^{5} \div {(\frac{x}{y})}^{5} = x^{10}$ C、 ${(a - b)}^{2} = a^{2} + 2 a b + b^{2}$ D、 $x^{3} y - x y^{3} = x y (x + y) (x - y)$

查看试题解析
7. 计算 $(a - \frac{1}{b}) \div (\frac{1}{a} - b)$ 的结果是（）

A、 $- \frac{a}{b}$ B、 $\frac{a}{b}$ C、 $- \frac{b}{a}$ D、 $\frac{b}{a}$

查看试题解析
8. 若代数式 $\frac{x^{2}}{x - 1} ◯ \frac{x}{x - 1} (x \neq 0)$ 运算结果为x，则在“○”处的运算符号应该是（）

A、除号“÷” B、除号“÷”或减号“-” C、减号“-” D、乘号“×”或减号“-”

查看试题解析
9. 计算 $\frac{a - 1}{a} + \frac{1}{a}$ 的结果为（　　）

A、1 B、﹣1 C、 $\frac{a + 2}{a}$ D、 $\frac{a - 2}{a}$

查看试题解析
10. 斑马线前“车让人”，不仅体现着一座城市对生命的尊重，也直接反映着城市的文明程度.如图，某路口的斑马线路段A—B—C横穿双向行驶车道，其中AB=BC=12米，在绿灯亮时，小敏共用22秒通过AC路段，其中通过BC路段的速度是通过AB路段速度的1.2倍，则小敏通过AB路段时的速度是（）

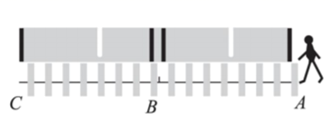A、0.5米/秒 B、1米/秒 C、1.5米/秒 D、2米/秒

查看试题解析

二、解答题（共8题；共66分）

11. 元旦，小红和弟弟小杰两人以包馄饨来庆祝成长，两人实际所包的馄饨数之比是5：3（小红：小杰），调皮的弟弟小杰从小红包好的馄饨里拿了2个放入自己的成果行列后，宣称自己和姐姐包好的馄饨数之比是2：3，求两人一共所包的馄饨数．（列分式方程解应用题）

查看试题解析
12. 已知关于 $x$ 的方程 $x = 2 x + 1$ 的解与方程 $\frac{x - a}{2} = 2 - \frac{x + 1}{3}$ 的解互为相反数，求 $a$ 的值．

查看试题解析
13. 某超市有线上和线下两种销售方式，经统计该超市苹果2021年5月份线上销售额为3000元，线下销售额为9000元，线下销售量比线上3倍少300千克，已知线下销售单价是线上销售单价的1.2倍，超市购入苹果单价为4元/千克，5月份该超市线上线下销售苹果的总利润为多少元？

查看试题解析
14. 根据疫情防控工作需要，某社区组织甲、乙两支医疗队开展疫苗接种工作，甲队比乙队每小时多接种30人，甲队接种2250人与乙队接种1800人用时相同，问甲队每小时接种多少人？

查看试题解析
15. 观察下面的变形规律：
$\frac{1}{1 \times 2} = 1 - \frac{1}{2} ； \frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3} ； \frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4} ； \frac{1}{4 \times 5} = \frac{1}{4} - \frac{1}{5} ；$ ……
解答下面的问题：

(1)、若n为正整数，请你猜想 $\frac{1}{n (n + 1)} =$ ；

(2)、计算： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \frac{1}{4 \times 5} + ⋯ + \frac{1}{2018 \times 2019} + \frac{1}{2019 \times 2020}$ .

(3)、分母中含有未知数的方程叫做分式方程.如 $\frac{2}{3 x} + \frac{4}{x} = \frac{7}{6}$ .
解法如下：
通分，得 $\frac{2}{3 x} + \frac{12}{3 x} = \frac{7}{6}$ ，
化简，得 $\frac{2 + 12}{3 x} = \frac{7}{6}$ ，
去分母，得14×6=21x，
解得x=4
分式方程要检验，当x=4时，原方程的分母不为0，所以x=4是原方程的解.
受第（1）问启发，请你解方程： $\frac{1}{x (x + 1)} + \frac{1}{x + 1} = 2$

查看试题解析
16. 解答下列各题：

(1)、解分式方程： $\frac{3}{1 - y} = \frac{y}{y - 1} - 5$

(2)、先化简，再求值：(2a−3)(3a+1)−6a(a−4)，其中 $a = \frac{2}{17}$

查看试题解析
17. 2021年是中国共产党成立100周年，为了让学生重温红色经典，传承革命精神，学校组织193名学生乘车去参观距学校6km的红色基地.现已预备了大客车和小客车共8辆，其中大客车每辆可坐51人，小客车每辆可坐8人，刚好都坐满.

(1)、学校预备了几辆大客车，几辆小客车？

(2)、为磨练自己意志，一部分学生改为步行前往红色基地，其余学生乘大客车出发，已知大客车速度是步行速度的6倍，他们同时出发，步行的学生晚50分钟到达基地，求步行的速度.

查看试题解析
18. 为了应对特殊时期，某口罩生产企业需要在若干天内加工 $12000$ 个口罩，在实际生产中，由于提高了生产技术水平，每天加工的个数为原来的 $1.5$ 倍，从而提前 $2$ 天完成任务

(1)、问该企业原计划每天生产多少个口罩？

(2)、如果该企业按原计划的工作效率加工了 $a$ 个口罩后，才将效率提高到原来的 $1.5$ 倍，则该企业完成这批口罩工作任务共用了多少天？（所得结果用含有 $a$ 的代数式表示： $a$ 为大于零的整数）

查看试题解析

三、填空题（共6题；共24分）

19. 若分式 $\frac{2 x - 3}{x + 1}$ 的值为0，则x的值为．

查看试题解析
20. 下列分式① $\frac{b}{8 a}$ ② $\frac{3 x^{2} y}{9 x y^{2}}$ ③ $\frac{a + b}{a - b}$ ④ $\frac{x - y}{x^{2} - y^{2}}$ ⑤ $\frac{x^{2} + x y}{2 x}$ 中，最简分式有（填正确答案的序号）．

查看试题解析
21. 计算： $\frac{3 a}{4 y} \cdot \frac{2 y^{2}}{3 a^{2}}$ ＝．

查看试题解析
22. 计算 $\frac{3 x + 3}{2 x^{2}} \div \frac{x^{2} - 1}{6 x}$ 的结果是．

查看试题解析
23. 化简： $\frac{3 y}{2 x - 2 y} + \frac{2 x y}{x^{2} - x y}$ 的计算结果是．

查看试题解析
24. 甲、乙两个搬运工搬运某种货物，已知乙比甲每小时多搬运600kg，甲搬运5000kg所用的时间与乙搬运8000kg所用的时间相等，求甲、乙两人每小时分别搬运多少kg货物。设甲每小时搬运xkg货物，则可列方程为。

查看试题解析