浙教版备考2022年中考数学二轮复习训练题7:四边形
试卷更新日期:2022-03-17 类型:二轮复习
一、单选题
-
1. 如图,已知▱OABC的顶点A,C分别在直线 和 上,O是坐标原点,则对角线OB长的最小值为( )
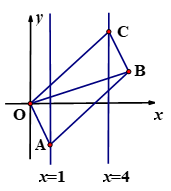 A、3 B、4 C、5 D、62. 如图,Rt△ABC中,∠ACB=90°,分别以AB,BC,AC为边在△ABC外部作正方形ADEB,CBFG,ACHI.将正方形ABED沿直线AB翻折,得到正方形ABE'D',AD'与CH交于点N,点E'在边FG上,D'E'与CG交于点M,记△ANC的面积为S1 , 四边形的面积为S2 , 若CN=2NH,S1+S2=14,则正方形ABED的面积为( )
A、3 B、4 C、5 D、62. 如图,Rt△ABC中,∠ACB=90°,分别以AB,BC,AC为边在△ABC外部作正方形ADEB,CBFG,ACHI.将正方形ABED沿直线AB翻折,得到正方形ABE'D',AD'与CH交于点N,点E'在边FG上,D'E'与CG交于点M,记△ANC的面积为S1 , 四边形的面积为S2 , 若CN=2NH,S1+S2=14,则正方形ABED的面积为( ) A、25 B、26 C、27 D、283. 如图,矩形 中, ,将矩形 绕点 旋转得到矩形 ,使点 的对应点 落在 上, 交 于点 ,在 上取点 ,使 .若 ,则 的长为( )
A、25 B、26 C、27 D、283. 如图,矩形 中, ,将矩形 绕点 旋转得到矩形 ,使点 的对应点 落在 上, 交 于点 ,在 上取点 ,使 .若 ,则 的长为( )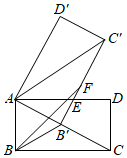 A、 B、 C、 D、4. 如图,在矩形 中,线段 , 分别平行于 , ,它们相交于点 ,点 , 分别在线段 , 上, , ,连接 , ,相交于点 .已知 , ,则 的值为( )
A、 B、 C、 D、4. 如图,在矩形 中,线段 , 分别平行于 , ,它们相交于点 ,点 , 分别在线段 , 上, , ,连接 , ,相交于点 .已知 , ,则 的值为( ) A、 B、 C、 D、5. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( )
A、 B、 C、 D、5. 如图,四边形ABCD中,∠ABC=120°,点F为CD中点,以AB,BD为边,AD为对角线作平行四边形ABDE,连接BE交AD于点O,且OF=BC=2,则AB的长为( ) A、 B、 C、 D、6. 如图,在▱ABCD中,过点A分别作AE⊥BC于点E,AF⊥CD于点F,分别作点C关于AB,AD的对称点G,H,连接CG,CH,AG,AH,GH.如果AB=30,∠EAF=30°,▱ABCD的面积为270 ,那么下列说法不正确的是( )
A、 B、 C、 D、6. 如图,在▱ABCD中,过点A分别作AE⊥BC于点E,AF⊥CD于点F,分别作点C关于AB,AD的对称点G,H,连接CG,CH,AG,AH,GH.如果AB=30,∠EAF=30°,▱ABCD的面积为270 ,那么下列说法不正确的是( )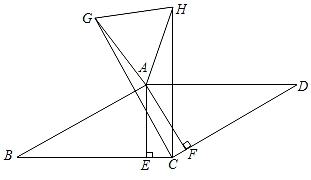 A、CE= CF B、∠GAH=60° C、GH=AF+CF D、△GCH的面积是▱ABCD的面积的一半7. 在平面直角坐标系中,已知四边形 各顶点坐标分别是: ,且 ,那么四边形 周长的最小值为( )A、 B、 C、 D、8. 将一张长宽分别为 和 的长方形纸片 按如图方式折叠,使点 分别落在长方形纸片内的点 处,折痕 分别交 于点 ,且满足 .喜欢探究的小明通过独立思考,得到两个结论:①当点 在一条直线上时, ;②当 时,四边形 是菱形.下列判断正确的是( )
A、CE= CF B、∠GAH=60° C、GH=AF+CF D、△GCH的面积是▱ABCD的面积的一半7. 在平面直角坐标系中,已知四边形 各顶点坐标分别是: ,且 ,那么四边形 周长的最小值为( )A、 B、 C、 D、8. 将一张长宽分别为 和 的长方形纸片 按如图方式折叠,使点 分别落在长方形纸片内的点 处,折痕 分别交 于点 ,且满足 .喜欢探究的小明通过独立思考,得到两个结论:①当点 在一条直线上时, ;②当 时,四边形 是菱形.下列判断正确的是( ) A、①正确,②错误 B、①错误,②正确 C、①,②都正确 D、①,②都错误9. 如图,点C,D是劣弧 上两点,CD∥AB,∠CAB=45°,若AB=6,CD=2,则 所在圆的半径长为( )
A、①正确,②错误 B、①错误,②正确 C、①,②都正确 D、①,②都错误9. 如图,点C,D是劣弧 上两点,CD∥AB,∠CAB=45°,若AB=6,CD=2,则 所在圆的半径长为( ) A、 B、 C、2 D、10. 如图,正方形ABCD中,AC与BD交于点O,M是对角线AC上的一个动点,直线BM与直线AD交于点E,过A作AH垂直BE于点H,直线AH与直线BD交于点N,连接EN、OH,则下列结论:①BM=AN;②OH平分∠MHN;③当EN∥OM时,BN2=DN•DB;④当M为AO中点时,= , 正确结论的个数有( )
A、 B、 C、2 D、10. 如图,正方形ABCD中,AC与BD交于点O,M是对角线AC上的一个动点,直线BM与直线AD交于点E,过A作AH垂直BE于点H,直线AH与直线BD交于点N,连接EN、OH,则下列结论:①BM=AN;②OH平分∠MHN;③当EN∥OM时,BN2=DN•DB;④当M为AO中点时,= , 正确结论的个数有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,正方形ABCD的边长为12,⊙B的半径为6,点P是⊙B上一个动点,则的最小值为.
 12. 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是.
12. 如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是. 13. 如图所示,已知矩形 中, , 现将边 绕它的一个端点旋转,当另一端点恰好落在边 所在直线的点E处时,线段 的长度为
13. 如图所示,已知矩形 中, , 现将边 绕它的一个端点旋转,当另一端点恰好落在边 所在直线的点E处时,线段 的长度为 14. 如图,在平行四边形ABCD中,点E是边AD上一点,CD=CE,连结BE,将△DCE 沿CE翻折,点D的对应点F恰好落在BE上,连结CF,若∠A=105°,△ABE的面积为 ,则ED= cm.
14. 如图,在平行四边形ABCD中,点E是边AD上一点,CD=CE,连结BE,将△DCE 沿CE翻折,点D的对应点F恰好落在BE上,连结CF,若∠A=105°,△ABE的面积为 ,则ED= cm.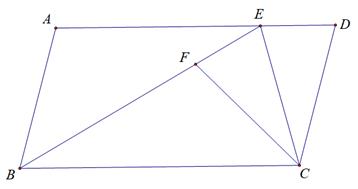 15. 如图,点 , 分别是矩形 的边 , 的中点,两条平行线 , 分别经过菱形 的顶点 , 和边 , 的中点 , ,已知菱形 的面积为 ,则图中阴影部分的面积和为 (用含 的代数式表示)
15. 如图,点 , 分别是矩形 的边 , 的中点,两条平行线 , 分别经过菱形 的顶点 , 和边 , 的中点 , ,已知菱形 的面积为 ,则图中阴影部分的面积和为 (用含 的代数式表示) 16. 如图,在正方形ABCD中,点E是AD的中点,点O是AC的中点,AC与BE交于点F,AG⊥BE,CH⊥BE,垂足分别为G,H,连接OH,OG,CG.下列结论:①CH﹣AG=HG;②AG=HG;③BH=OG;④AF∶OF∶OC=2∶1∶3;⑤5S△AFG=S△GHC;⑥OG•AC=BH•CD.其中结论正确的序号是 .
16. 如图,在正方形ABCD中,点E是AD的中点,点O是AC的中点,AC与BE交于点F,AG⊥BE,CH⊥BE,垂足分别为G,H,连接OH,OG,CG.下列结论:①CH﹣AG=HG;②AG=HG;③BH=OG;④AF∶OF∶OC=2∶1∶3;⑤5S△AFG=S△GHC;⑥OG•AC=BH•CD.其中结论正确的序号是 .
三、解答题
-
17. 矩形ABCD的周长为28(AB<BC),对角线AC与BD相交于点O,对角线长为10,过点O作OP⊥BD,且OP=AO,过点P作PE⊥BC,垂足为E,请画出正确的图形,并直接写出线段CE的长.
四、综合题
-
18. 问题背景:
如图1,在矩形中, , , 点E是边AB的中点,过点作交BD于点F.
 (1)、实验探究:
(1)、实验探究:在一次数学活动中,小王同学将图1中的绕点按逆时针方向旋转 , 如图2所示,得到结论:①;②直线AE与DF所夹锐角的度数为 .
(2)、小王同学继续将绕点B按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立?并说明理由.(3)、拓展延伸:在以上探究中,当旋转至、、三点共线时,则的面积为 .
19. 定义:如果一个三角形一条边上的高与这条边的比值叫做这条边所对角的准对(记作qad).如图1,在△ABC中,AH⊥BC于点H,则qad∠BAC=.当qad∠BAC=时,则称∠BAC为这个三角形的“金角”.已知在矩形ABCD中,AB=3,BC=6,△ACE的“金角”∠EAC所对的边CE在BC边上,将△ACE绕点C按顺时针方向旋转α(0°<α<90°)得到△A'CE',A'C交AD边于点F. (1)、如图2,当α=45°时,求证:∠ACF是“金角”.(2)、如图3,当点E'落在AD边上时,求qad∠AFC的值.20. 已知,如图,在平面直角坐标系中,正方形ABCD,点A(0,10),点B(8,4),点C在第一象限,点P从顶点A出发,沿着正方形的边长逆时针运动一周,在OP右侧作∠OPQ=∠OAB交x轴于点Q.
(1)、如图2,当α=45°时,求证:∠ACF是“金角”.(2)、如图3,当点E'落在AD边上时,求qad∠AFC的值.20. 已知,如图,在平面直角坐标系中,正方形ABCD,点A(0,10),点B(8,4),点C在第一象限,点P从顶点A出发,沿着正方形的边长逆时针运动一周,在OP右侧作∠OPQ=∠OAB交x轴于点Q. (1)、求点C坐标.(2)、当点P与点B重合时,求OQ的长.(3)、在点P的整个运动过程中,当△OPQ是以PQ为腰的等腰三角形时,求OQ的长.21. 如图,把长方形ABCD绕点A按逆时针方向旋转得到长方形AEFG,使点E落在对角线BD上,连接DG,DF.
(1)、求点C坐标.(2)、当点P与点B重合时,求OQ的长.(3)、在点P的整个运动过程中,当△OPQ是以PQ为腰的等腰三角形时,求OQ的长.21. 如图,把长方形ABCD绕点A按逆时针方向旋转得到长方形AEFG,使点E落在对角线BD上,连接DG,DF. (1)、若∠BAE=50°,求∠DGF的度数;(2)、求证:DF = DC;(3)、若S△ABE+S△DFG = S△ADG , 直接写出 的值.22. 如图,在矩形ABCD中,AB:BC=3:2,点F、G分别在边AB、CD上,将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形EFGP,EP交CD于点H,连接AE交GF于点O.
(1)、若∠BAE=50°,求∠DGF的度数;(2)、求证:DF = DC;(3)、若S△ABE+S△DFG = S△ADG , 直接写出 的值.22. 如图,在矩形ABCD中,AB:BC=3:2,点F、G分别在边AB、CD上,将矩形ABCD沿GF折叠,使点A落在BC边上的点E处,得到四边形EFGP,EP交CD于点H,连接AE交GF于点O. (1)、若BC=8,E是BC中点,求BF的长;(2)、试探究GF与AE之间的位置关系与数量关系,并说明理由;(3)、连接CP,若 ,GF=2 ,求线段BE和CP的长.23. 在菱形中, , .点E为平面内一动点,.
(1)、若BC=8,E是BC中点,求BF的长;(2)、试探究GF与AE之间的位置关系与数量关系,并说明理由;(3)、连接CP,若 ,GF=2 ,求线段BE和CP的长.23. 在菱形中, , .点E为平面内一动点,.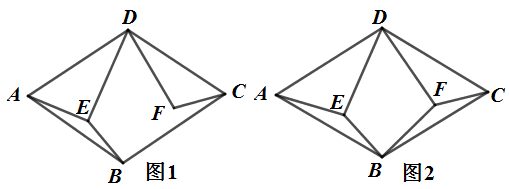
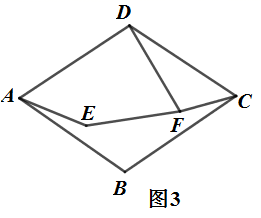 (1)、当点E在菱形内部时,如图1,连接 , , 将线段绕点D逆时针转得线段 , 连接.
(1)、当点E在菱形内部时,如图1,连接 , , 将线段绕点D逆时针转得线段 , 连接.①求证:;
②如图2,连接 , 若 , 求四边形的面积;
(2)、如图3,若 , , 当点E在平面内运动时,连接 , 取的中点F,连接 , 则的最大值为.(直接写出结果)24. 已知正方形ABCD与正方形AEFG,正方形AEFG绕点A旋转一周. (1)、如图①,连接BG、CF,求 的值;(2)、当正方形AEFG旋转至图②位置时,连接CF、BE,分别去CF、BE的中点M、N,连接MN、试探究:MN与BE的关系,并说明理由;(3)、连接BE、BF,分别取BE、BF的中点N、Q,连接QN,AE=6,请直接写出线段QN扫过的面积.
(1)、如图①,连接BG、CF,求 的值;(2)、当正方形AEFG旋转至图②位置时,连接CF、BE,分别去CF、BE的中点M、N,连接MN、试探究:MN与BE的关系,并说明理由;(3)、连接BE、BF,分别取BE、BF的中点N、Q,连接QN,AE=6,请直接写出线段QN扫过的面积.
-