浙江省绍兴市柯桥区2021-2022学年八年级上学期期末数学试卷
试卷更新日期:2022-03-17 类型:期末考试
一、单选题
-
1. 下列图案中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若 ,则下列各式中,一定成立的是( )A、 B、 C、 D、3.
2. 若 ,则下列各式中,一定成立的是( )A、 B、 C、 D、3.如图,在生活中,我们经常会看见如图所示的情况,在电线杆上拉两条钢筋,来加固电线杆,这是利用了三角形的( )
 A、稳定性 B、灵活性 C、对称性 D、全等性4. 在平面直角坐标系中,将点 向左平移3个单位后得到的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 不等式 的解在数轴上表示为( )A、
A、稳定性 B、灵活性 C、对称性 D、全等性4. 在平面直角坐标系中,将点 向左平移3个单位后得到的点位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 不等式 的解在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 6. 如图,已知AB=AD,AC=AE,若要判定△ABC≌△ADE,则下列添加的条件中正确的是( )
6. 如图,已知AB=AD,AC=AE,若要判定△ABC≌△ADE,则下列添加的条件中正确的是( ) A、∠1=∠DAC B、∠B=∠D C、∠1=∠2 D、∠C=∠E7. 已知点 , 在一次函数 的图象上,则 , 的大小关系是( )A、 B、 C、 D、以上都不对8. 如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )
A、∠1=∠DAC B、∠B=∠D C、∠1=∠2 D、∠C=∠E7. 已知点 , 在一次函数 的图象上,则 , 的大小关系是( )A、 B、 C、 D、以上都不对8. 如图是某蓄水池的横断面的示意图,分深水区和浅水区,如果向这个蓄水池中以固定的水流量(单位时间注水的体积)注水(注满水后停止注水),那么下列图中能大致表示水的深度 h 与注水时间 t 之间关系的图象的是( )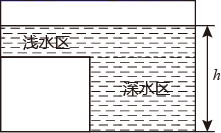 A、
A、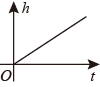 B、
B、 C、
C、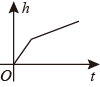 D、
D、 9. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点 ,第二次运动到点 ,第三次运动到 ,…,按这样的运动规律,第2022次运动后,动点 的坐标是( )
9. 如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第一次从原点O运动到点 ,第二次运动到点 ,第三次运动到 ,…,按这样的运动规律,第2022次运动后,动点 的坐标是( ) A、 B、 C、 D、10. 如图,三角形纸片ABC,点D是BC边上一点,连结AD,把 沿着AD翻折,得到 ,DE与AC交于点F.若点F是DE的中点, , , 的面积为9,则点F到BC的距离为( )
A、 B、 C、 D、10. 如图,三角形纸片ABC,点D是BC边上一点,连结AD,把 沿着AD翻折,得到 ,DE与AC交于点F.若点F是DE的中点, , , 的面积为9,则点F到BC的距离为( ) A、1.4 B、2.4 C、3.6 D、4.8
A、1.4 B、2.4 C、3.6 D、4.8二、填空题
-
11. 为说明命题“如果 ,那么 ”是假命题,你举出的一个反例是.12. 在平面直角坐标系中,点 到y轴的距离是.13. 三角形的三边长分别为3,4,5,则最长边上的高为 .14. 一副直角三角板,按如图方式叠放在一起,其中 , ,若 ,则 等于度.
 15. 《九章算术》中的“引葭赴岸”问题:今有池方一丈,葭(一种芦苇类植物)生其中央,出水一尺.引葭赴岸,适与岸齐,水深几何?其大意是:有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面1尺.如果把该芦苇拉向岸边,那么芦苇的顶部恰好碰到岸边(如图所示),则水深尺.
15. 《九章算术》中的“引葭赴岸”问题:今有池方一丈,葭(一种芦苇类植物)生其中央,出水一尺.引葭赴岸,适与岸齐,水深几何?其大意是:有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面1尺.如果把该芦苇拉向岸边,那么芦苇的顶部恰好碰到岸边(如图所示),则水深尺. 16. 如图,直线y=x+2与直线y=ax+c相交于点P(m,3).则关于x的不等式x+2≥ax+c的不等式的解为 .
16. 如图,直线y=x+2与直线y=ax+c相交于点P(m,3).则关于x的不等式x+2≥ax+c的不等式的解为 .
 17. 如图,在边长为4的等边三角形ABC中,D,E分别是边BC,AC的中点, 于点F,连结EF,则EF的长为.
17. 如图,在边长为4的等边三角形ABC中,D,E分别是边BC,AC的中点, 于点F,连结EF,则EF的长为. 18. 新定义:[a,b]为一次函数 (a≠0,a、b为实数)的“关联数”.若“关联数”为[3,m-2] 的一次函数是正比例函数,则点(1-m,1+m)在第象限.19. 定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是.
18. 新定义:[a,b]为一次函数 (a≠0,a、b为实数)的“关联数”.若“关联数”为[3,m-2] 的一次函数是正比例函数,则点(1-m,1+m)在第象限.19. 定义:在平面直角坐标系中,把从点P出发沿横或纵方向到达点Q(至多拐一次弯)的路径长称为P,Q的“实际距离”.如图,若 , ,则P,Q的“实际距离”为5,即 或 .环保低碳的公共自行车,逐渐成为市民出行喜欢的交通工具.设A,B,C三个小区的坐标分别为 , , ,若点M表示公共自行车停放点,且满足M到A,B,C的“实际距离”相等,则点M的坐标是. 20. 如图,AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于点E,F,G分别是线段AB和线段AC上的动点,且AF=CG,若DE=1,AB=2,则DF+DG的最小值为.
20. 如图,AB∥CD,AC平分∠BAD,BD平分∠ADC,AC和BD交于点E,F,G分别是线段AB和线段AC上的动点,且AF=CG,若DE=1,AB=2,则DF+DG的最小值为.
三、解答题
-
21. 解下列不等式组:(1)、2(x+1)>3x﹣4(2)、22. 如图,方格纸中的每个小方格都是边长为1个单位的小正方形,每个小正方形的顶点称为格点,△ABC的顶点都在格点上,建立平面直角坐标系后,点A,B,C的坐标分别为(1,1),(4,2),(2,3).
 (1)、画出△ABC向左平移4个单位,再向上平移1个单位后得到的△A1B1C1;(2)、画出△ABC向关于x轴对称的△A2B2C2;(3)、以点A、A1、A2为顶点的三角形的面积为.23. 为了倡导居民节约用水,生活用水按阶梯式水价计费,如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象,请根据图象所提供的信息,解答下列问题:
(1)、画出△ABC向左平移4个单位,再向上平移1个单位后得到的△A1B1C1;(2)、画出△ABC向关于x轴对称的△A2B2C2;(3)、以点A、A1、A2为顶点的三角形的面积为.23. 为了倡导居民节约用水,生活用水按阶梯式水价计费,如图是居民每户每月的水费y(元)与所用的水量x(吨)之间的函数图象,请根据图象所提供的信息,解答下列问题: (1)、当用水量不超过10吨时,每吨水收费元.(2)、当用水量超过10吨且不超过30吨时,求y与x之间的函数表达式;(3)、某户居民四、五月份水费共85元,五月份用水比四月份多5吨,求这户居民四月份用水多少吨.24. 如图,在 中, , , ,CD与BE相交于点F.
(1)、当用水量不超过10吨时,每吨水收费元.(2)、当用水量超过10吨且不超过30吨时,求y与x之间的函数表达式;(3)、某户居民四、五月份水费共85元,五月份用水比四月份多5吨,求这户居民四月份用水多少吨.24. 如图,在 中, , , ,CD与BE相交于点F. (1)、求证: ;(2)、若 , ,求 的面积.25. 为了做好“新冠肺炎”疫情防控工作,柯桥区某校准备购买一批消毒液.已知A型消毒液和B型消毒液的单价分别是12元和8元.需购买这两种消毒液共300瓶,并且购买A型消毒液的数量要少于B型消毒液数量的 ,但又不少于B型消毒液数量的 .设买A型消毒液x瓶,买两种消毒液的总费用为y元.(1)、写出y(元)关于x(瓶)的函数关系式,并求出自变量x的取值范围.(2)、购买这两种消毒液各多少瓶时,费用最少?最少的费用是多少元?26.
(1)、求证: ;(2)、若 , ,求 的面积.25. 为了做好“新冠肺炎”疫情防控工作,柯桥区某校准备购买一批消毒液.已知A型消毒液和B型消毒液的单价分别是12元和8元.需购买这两种消毒液共300瓶,并且购买A型消毒液的数量要少于B型消毒液数量的 ,但又不少于B型消毒液数量的 .设买A型消毒液x瓶,买两种消毒液的总费用为y元.(1)、写出y(元)关于x(瓶)的函数关系式,并求出自变量x的取值范围.(2)、购买这两种消毒液各多少瓶时,费用最少?最少的费用是多少元?26. (1)、 是边长为6的等边三角形,E是边AC上的一点,且 ,小明以BE为边作等边三角形BEF,如图①,求CF的长;(2)、 是边长为6的等边三角形,E是边AC上的一个动点,小明以BE为边作等边三角形BEF,如图②,在点E从点C到点A的运动过程中,求点F所经过的路径长;(3)、 是边长为6的等边三角形,M是高CD上的一个动点,小明以BM为边作等边三角形BMN,如图③,在点M从点C到点D的运动过程中,求点N所经过的路径长.
(1)、 是边长为6的等边三角形,E是边AC上的一点,且 ,小明以BE为边作等边三角形BEF,如图①,求CF的长;(2)、 是边长为6的等边三角形,E是边AC上的一个动点,小明以BE为边作等边三角形BEF,如图②,在点E从点C到点A的运动过程中,求点F所经过的路径长;(3)、 是边长为6的等边三角形,M是高CD上的一个动点,小明以BM为边作等边三角形BMN,如图③,在点M从点C到点D的运动过程中,求点N所经过的路径长.