浙江省金华市武义县2020-2021学年八年级下学期期中数学试卷
试卷更新日期:2022-03-17 类型:期中考试
一、单选题
-
1. 若二次根式 有意义,则 的取值范围是( )A、 B、 C、 D、2. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若平行四边形的一边长为 , 则它的两条对角线长可以是( )A、和 B、和 C、和 D、和4. 若关于x的一元二次方程 有两个不相等的实数根,则实数m的取值范围是( )A、 B、 C、 且 D、5. 有一组数据、、、、 , 它的方差是( )A、 B、 C、 D、6. △ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )A、4.5 B、9 C、10 D、127. 用反证法证明:“三角形三内角中至少有一个角不大于60°”时,第一步应是( )A、假设三角形三内角中至多有一个角不大于60° B、假设三角形三内角中至少有一个角不小于60° C、假设三角形三内角都大于60° D、假设三角形三内角中至少有一个角大于60°8. 如图,矩形 中,点 在 上,且 平分 , , ,则矩形 的面积为( )
3. 若平行四边形的一边长为 , 则它的两条对角线长可以是( )A、和 B、和 C、和 D、和4. 若关于x的一元二次方程 有两个不相等的实数根,则实数m的取值范围是( )A、 B、 C、 且 D、5. 有一组数据、、、、 , 它的方差是( )A、 B、 C、 D、6. △ABC中,AB=7,BC=6,AC=5,点D、E、F分别是三边的中点,则△DEF的周长为( )A、4.5 B、9 C、10 D、127. 用反证法证明:“三角形三内角中至少有一个角不大于60°”时,第一步应是( )A、假设三角形三内角中至多有一个角不大于60° B、假设三角形三内角中至少有一个角不小于60° C、假设三角形三内角都大于60° D、假设三角形三内角中至少有一个角大于60°8. 如图,矩形 中,点 在 上,且 平分 , , ,则矩形 的面积为( )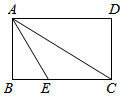 A、 B、24 C、 D、129. 如图,在▱ABCD中,BC=6 ,∠A=135°,S▱ABCD=12 .若点E、F分别在边BC、AD上,且AF=CE,∠EFD=30°,则AF的长为( )
A、 B、24 C、 D、129. 如图,在▱ABCD中,BC=6 ,∠A=135°,S▱ABCD=12 .若点E、F分别在边BC、AD上,且AF=CE,∠EFD=30°,则AF的长为( )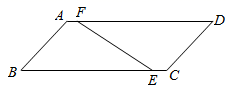 A、 ﹣1 B、2 ﹣1 C、6 ﹣6 D、4 ﹣210. 如图,已知 , 分别为正方形的边 , 的中点,与交于点 , 为的中点,则下列结论:① , ② , ③ , ④.其中正确结论的有( )
A、 ﹣1 B、2 ﹣1 C、6 ﹣6 D、4 ﹣210. 如图,已知 , 分别为正方形的边 , 的中点,与交于点 , 为的中点,则下列结论:① , ② , ③ , ④.其中正确结论的有( ) A、个 B、个 C、个 D、个
A、个 B、个 C、个 D、个二、填空题
-
11. 若一个多边形的内角和是外角和的2倍,则它的边数是 .12. 是方程的一个根,则代数式的值是.13. 已知菱形中, , 则.14. 如图,已知菱形OABC的顶点O(0,0),B(2,2),每秒旋转45°,则第60秒时,菱形的对角线交点D的坐标为 .
 15. 如图,若:、、的面积分别为、、 , 则阴影部分的面积是.
15. 如图,若:、、的面积分别为、、 , 则阴影部分的面积是. 16. 如图,点P是线段AB上的一个点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,点M,N分别是对角线AC,BE的中点,连接MN,PM,PN,若∠DAP=60°,AP2+3PB2=5, 则线段MN的长为。
16. 如图,点P是线段AB上的一个点,分别以AP,PB为边在AB的同侧作菱形APCD和菱形PBFE,点P,C,E在一条直线上,点M,N分别是对角线AC,BE的中点,连接MN,PM,PN,若∠DAP=60°,AP2+3PB2=5, 则线段MN的长为。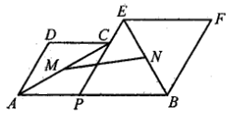
三、解答题
-
17. 计算:(1)、(2)、.18. 解方程:(1)、(2)、 .19. 某学校抽查了某班级某月5天的用电量,数据如下表(单位:度):
度数
天数
(1)、求这天的用电量的平均数;(2)、求这天用电量的众数、中位数;(3)、学校共有个班级,若该月按天计,试估计该校该月的总用电量.20. 如图,在 中, 平分 交 于点M.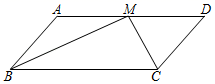 (1)、若 ,求 的长;(2)、若 是 的中点,连结 ,求证: 平分21. 如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)、若 ,求 的长;(2)、若 是 的中点,连结 ,求证: 平分21. 如图,四边形ABCD是平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.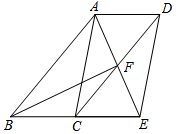 (1)、求证:BE=CD;(2)、若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.22. 如图1,有一张长 宽 的长方形硬纸片,裁去角上 个小正方形和 个小长方形(图中阴影部分)之后,恰好折成如图2的有盖纸盒.
(1)、求证:BE=CD;(2)、若BF恰好平分∠ABE,连接AC、DE,求证:四边形ACED是平行四边形.22. 如图1,有一张长 宽 的长方形硬纸片,裁去角上 个小正方形和 个小长方形(图中阴影部分)之后,恰好折成如图2的有盖纸盒.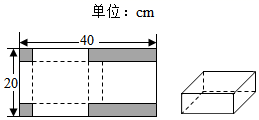 (1)、若纸盒的高是 cm,求纸盒底面长方形的长和宽;(2)、若纸盒的底面积是 ,求纸盒的高.23. 定义:如果一个四边形的一边垂直于相邻两边,且该边中点到对边的距离等于该边边长的一半,我们就称这个四边形为“平衡四边形”.如图 , 在四边形中, , , 是的中点,于点 , 且 , 则四边形是“平衡四边形”,点为“平衡四边形”的“平衡点”.
(1)、若纸盒的高是 cm,求纸盒底面长方形的长和宽;(2)、若纸盒的底面积是 ,求纸盒的高.23. 定义:如果一个四边形的一边垂直于相邻两边,且该边中点到对边的距离等于该边边长的一半,我们就称这个四边形为“平衡四边形”.如图 , 在四边形中, , , 是的中点,于点 , 且 , 则四边形是“平衡四边形”,点为“平衡四边形”的“平衡点”. (1)、【定义理解】
(1)、【定义理解】
下列图形中,属于“平衡四边形”的是____ .A、 B、
B、 C、
C、 D、
D、 (2)、【性质探究】
(2)、【性质探究】
如图 , 在“平衡四边形”中,点是它的“平衡点”,则有下列性质:①;②.请证明上述两条性质.
 (3)、【性质应用】
(3)、【性质应用】
如图 , 在“平衡四边形”中, , , 求的长. 24. 如图,在平面直角坐标系中,已知 的两直角边 , 分别在 轴, 轴的正半轴上( ),且 , 的长分别是一元二次方程 的两个根,线段 的垂直平分线 交 于点 ,分别交 轴, 轴于点 , .
24. 如图,在平面直角坐标系中,已知 的两直角边 , 分别在 轴, 轴的正半轴上( ),且 , 的长分别是一元二次方程 的两个根,线段 的垂直平分线 交 于点 ,分别交 轴, 轴于点 , . (1)、求点 、 的坐标(2)、求线段 的长(3)、已知 是直线 上一个动点,点 是直线 上一个动点,则在坐标平面内是否存在点 ,使得以点 、 、 、 为顶点的四边形是以5为边长的正方形?若存在,直接写出点 的坐标;若不存在,说明理由.
(1)、求点 、 的坐标(2)、求线段 的长(3)、已知 是直线 上一个动点,点 是直线 上一个动点,则在坐标平面内是否存在点 ,使得以点 、 、 、 为顶点的四边形是以5为边长的正方形?若存在,直接写出点 的坐标;若不存在,说明理由.