浙江省绍兴市诸暨市浣东教育共同体2020-2021学年八年级下学期期中数学试卷
试卷更新日期:2022-03-17 类型:期中考试
一、单选题
-
1. 下列方程中是关于x一元二次方程的是( ).A、 B、 C、 D、2. 将如图的七巧板的其中几块,拼成一个多边形,为中心对称图形的是( )
 A、
A、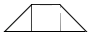 B、
B、 C、
C、 D、
D、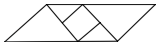 3. 要使式子有意义,则x的取值范围是( ).A、 B、 C、 D、4. 若与关于坐标原点成中心对称,则a,b分别为( ).A、4,3 B、-4,3 C、4,-3 D、-4,-35. 在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数6. 王老师对甲、乙两人五次数学成绩进行统计,两人平均成绩均为90分,方差S甲2=12,S乙2=51,则下列说法正确的是( )A、甲、乙两位同学的成绩一样稳定 B、乙同学的成绩更稳定 C、甲同学的成绩更稳定 D、不能确定7. 不能判定一个四边形是平行四边形的条件是()
3. 要使式子有意义,则x的取值范围是( ).A、 B、 C、 D、4. 若与关于坐标原点成中心对称,则a,b分别为( ).A、4,3 B、-4,3 C、4,-3 D、-4,-35. 在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、众数 B、方差 C、平均数 D、中位数6. 王老师对甲、乙两人五次数学成绩进行统计,两人平均成绩均为90分,方差S甲2=12,S乙2=51,则下列说法正确的是( )A、甲、乙两位同学的成绩一样稳定 B、乙同学的成绩更稳定 C、甲同学的成绩更稳定 D、不能确定7. 不能判定一个四边形是平行四边形的条件是()
A、两组对边分别平行 B、一组对边平行,另一组对边相等 C、一组对边平行且相等 D、两组对边分别相等8. 用反证法证明:“直角三角形至少有一个锐角不小于45°”时,应先假设( )A、直角三角形的每个锐角都小于45° B、直角三角形有一个锐角大于45° C、直角三角形的每个锐角都大于45° D、直角三角形有一个锐角小于45°9. 如图,在四边形ABCD中,∠ABC=90°,AB=BC=2 , E、F分别是AD、CD的中点,连接BE、BF、EF,若四边形ABCD的面积为6,则△BEF的面积为( )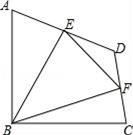 A、2 B、 C、 D、310. 在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )A、11+ B、11- C、11+ 或11- D、11- 或1+
A、2 B、 C、 D、310. 在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,作AF垂直于直线CD于点F,若AB=5,BC=6,则CE+CF的值为( )A、11+ B、11- C、11+ 或11- D、11- 或1+二、填空题
-
11. 当时,二次根式.12. 一个多边形的内角和是它的外角和的4倍,则这个多边形的边数是 .13. 已知 , 则.14. 前段时间,李克强总理就高血压,糖尿病的用药50%纳入报销的视频在各大网站频频报道,现有某治高血压药原来售价100元每瓶,为促进医疗改革连续两次降价后售价为81元每瓶,若每次下降的百分率相同,则这个百分率是.15. 若m是的一个实数根,则.16. 已知 , , 在平面直角坐标找一点D,使以A、B、C、D四点的四边形为平行四边形,则D点的坐标是.
三、解答题
-
17. 化简:(1)、(2)、18. 解方程:(1)、(2)、19. 如图,的三个顶点都在正方形网格的格点上,其中点A的坐标为.
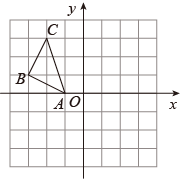
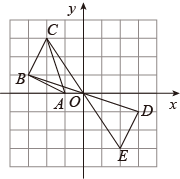 (1)、在网格中作 , 使与关于原点O成中心对称.(2)、如果四边形是以为一边,且两条对角线相交于原点O的平行四边形,请你直接写出点D和点E的坐标.20. 我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
(1)、在网格中作 , 使与关于原点O成中心对称.(2)、如果四边形是以为一边,且两条对角线相交于原点O的平行四边形,请你直接写出点D和点E的坐标.20. 我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.平均分(分)
中位数(分)
众数(分)
方差(分2)
初中部
a
85
b
高中部
85
c
100
160
 (1)、根据图示计算出a、b、c的值;(2)、结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?(3)、计算初中代表队决赛成绩的方差 , 并判断哪一个代表队选手成绩较为稳定.21. 清明节期间,某食品店平均每天可卖出300只艾饺,卖出1只艾饺的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只艾饺.为了使每天获取的利润更多,该店决定把零售单价下降m()元.(1)、在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,并且卖出的艾饺更多?(2)、在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润最大?最大利润是多少?22. 已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣)=0.(1)、判断这个一元二次方程的根的情况;(2)、若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.23. 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)、根据图示计算出a、b、c的值;(2)、结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?(3)、计算初中代表队决赛成绩的方差 , 并判断哪一个代表队选手成绩较为稳定.21. 清明节期间,某食品店平均每天可卖出300只艾饺,卖出1只艾饺的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只艾饺.为了使每天获取的利润更多,该店决定把零售单价下降m()元.(1)、在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,并且卖出的艾饺更多?(2)、在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润最大?最大利润是多少?22. 已知关于x的一元二次方程x2﹣(2k+1)x+4(k﹣)=0.(1)、判断这个一元二次方程的根的情况;(2)、若等腰三角形的一边长为3,另两条边的长恰好是这个方程的两个根,求这个等腰三角形的周长及面积.23. 已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.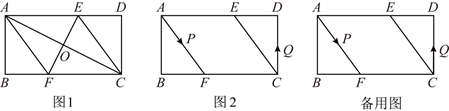 (1)、如图1,连接AF、CE求证:四边形AFCE为菱形;(2)、如图1,求AF的长;(3)、如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
(1)、如图1,连接AF、CE求证:四边形AFCE为菱形;(2)、如图1,求AF的长;(3)、如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.