浙江省浣江教育共同体2020-2021学年八年级下学期期中检测数学试卷

试卷更新日期：2022-03-17 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个交通标志中，是中心对称图形的标志是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{\sqrt{x + 1}}{x - 2}$ 有意义，则实数x的取值范围是（）

A、x≥﹣1且x≠0 B、x≥﹣1 C、x＞﹣1 D、x≥﹣1且x≠2

查看试题解析
3. 用反证法证明“四边形中至少有一个内角大于或等于90°”时，应先假设（）

A、有一个内角小于90° B、每一个内角都大于90° C、有一个内角小于或等于90° D、每一个内角都小于90°

查看试题解析
4. 如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使四边形AECF是平行四边形，则添加的条件不能是（）

A、BE＝FD B、AE＝CF C、BF＝DE D、∠1＝∠2

查看试题解析
5. 若一组数据x₁ ， x₂ ， …，xn的平均数为16，方差为2，则另一组数据x₁+3，x₂+3，…xn+3的平均数和方差分别为（）

A、19，2 B、19，3 C、16，2 D、16，3

查看试题解析
6. 若关于x的一元二次方程 $(m - 1) x^{2} + 2 x - 2 = 0$ 有两个不相等的实数根，则实数m的取值范围是（）

A、 $m < \frac{1}{2}$ B、 $m > \frac{1}{2}$ C、 $m > \frac{1}{2}$ 且 $m \neq 1$ D、 $m \neq 1$

查看试题解析
7. 如图，商用手扶梯AB的坡比为1： $\sqrt{3}$ ，已知扶梯的长AB为10米，则小明乘坐扶梯从B处到A处的水平距离BC的长为（）

A、5米 B、5 $\sqrt{3}$ 米 C、10米 D、10 $\sqrt{3}$ 米

查看试题解析
8. 如图，在一块长为16m，宽为8m的矩形ABCD空地内修建四条宽度相等，且与矩形各边垂直的道路，四条道路围成的中间部分恰好是一个正方形，且边长是道路宽的3倍，道路占地总面积为30m² ，设道路宽为xm，则以下方程正确的是（）

A、24x+6x²＝30 B、24x+3x²＝30 C、48x﹣6x²＝30 D、48x﹣3x²＝30

查看试题解析
9. 如图，在 $▱ A B C D$ 中，点 $F$ 是线段 $C D$ 上一动点，过点 $A$ 作 $▱ B F G E$ ，当点 $F$ 从点 $C$ 向点 $D$ 运动过程中，四边形 $B F G E$ 的面积的变化情况是（）

A、保持不变 B、一直减小 C、一直增大 D、先增大后减小

查看试题解析
10. 如图， $▱ A B C D$ 中， $A B \neq B C$ ， F是 $B C$ 上一点， $A E$ 平分 $∠ F A D$ ，且E是 $C D$ 的中点，则下列结论：① $A E ⊥ E F$ ， ② $A F = C F + C D$ ， ③ $A F = C F + A D$ ， ④ $A B = B F$ ，其中正确的是（）

A、②④ B、①② C、①③ D、①②④

查看试题解析

二、填空题

11. 若一组数据2，3，x，5，6的平均数为4，则这组数据的方差为.

查看试题解析
12. 若一个多边形每一个外角都等于36°，则这个多边形有条边.

查看试题解析
13. 若1＜x＜2，则 $| x - 1 | + \sqrt{{(x - 2)}^{2}}$ 的值为.

查看试题解析
14. 对于实数a，b，定义运算“*”，a*b＝ ${\begin{array}{l} a^{2} - a b (a > b) \\ a b - b^{2} (a \leq b) \end{array}$ 例如4*2.因为4＞2，所以4*2＝4²﹣4×2＝8，若x₁ ， x₂是一元二次方程x²﹣7x+12＝0的两个根，则x₁*x₂＝.

查看试题解析
15. 如图，平行四边形 $A B C D$ 的对角线 $A C 、 B D$ 相交于点 $O ，$ 点 $E ， F$ 分别是线段 $A O 、 B O$ 的中点，若 $A C + B D = 24 c m$ ， $E F = 4 c m$ .则 $△ O C D$ 的周长等于 $c m$ .

查看试题解析
16. 如图，已知平行四边形ABCD中，∠BCD的平分线交边AD于E，∠ABC的平分线交AD于F，若AB＝12，AE＝5，则AD＝.

查看试题解析
17. 等腰三角形的三边长分别为a，b，2，且a，b是关于x的一元二次方程x²﹣8x+n﹣2＝0的两根，则n的值为.

查看试题解析
18. 如图，△ABC的周长为25，点D，E都在边BC上，∠ABC的平分线垂直于AE，垂足为Q，∠ACB的平分线垂直于AD，垂足为P，若BC＝10，则PQ的长.

查看试题解析
19. 如图，平面直角坐标系中，▱OABC的顶点A坐标为（6，0），C点坐标为（2，2），若直线y＝kx+2平分▱OABC的周长，则k的值为.

查看试题解析
20. 如图，△ABC中，AB＝AC＝10，BC＝12，D为AC边上一动点，E为平面内一点，以点B、C、D、E为顶点的四边形为平行四边形，则DE的最小值为.

查看试题解析

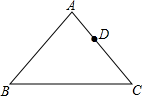
三、解答题

21. 计算：

(1)、 $\sqrt{{(- 2)}^{2}} + | \sqrt{3} - 2 | - \sqrt{27} \times \sqrt{\frac{1}{3}}$

(2)、 ${(\sqrt{2} + \sqrt{3})}^{2} - \sqrt{24}$

查看试题解析
22. 解下列方程

(1)、（3x＋2）²＝4；

(2)、3x²＋1＝4x.

查看试题解析

23. 为选拔参加八年级数学“拓展性课程”活动人选，数学李老师对本班甲、乙两名学生以前经历的10次测验成绩（分）进行了整理、分析（见图①）：

学生	平均数	中位数	众数	方差
甲	83.7	a	86	13.21
乙	83.7	82	b	46.21

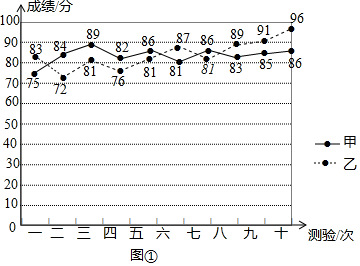(1)、写出a，b的值；

(2)、如要推选1名学生参加，你推荐谁？请说明你推荐的理由.

查看试题解析

24. 如图，四边形ABCD是平行四边形，∠BAD的角平分线AE交CD于点F，交BC的延长线于点E.

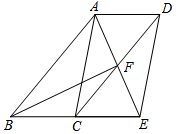(1)、求证：BE＝CD；

(2)、若BF恰好平分∠ABE，连接AC、DE，求证：四边形ACED是平行四边形.

查看试题解析
25. 春秋旅行社为吸引市民组团去天水湾风景区旅游，推出了如下收费标准：

某单位组织员工去天水湾风景区旅游，共支付给春秋旅行社旅游费用27000元，请问该单位这次共有多少员工去天水湾风景区旅游？

查看试题解析
26. 如图，在▱ABCD中，对角线AC，BD相交于点O，AB⊥AC，AB＝6cm，BC＝10cm.点P从A点出发沿AD方向匀速运动，速度为1cm/s.连接PO并延长交BC于点Q，设运动时间为t（0＜t＜10）.

(1)、当t为何值时，四边形ABQP是平行四边形？

(2)、设四边形OQCD的面积为y（cm²），求y与t之间的函数关系式；

(3)、是否存在某一时刻t，使点O在线段AP的垂直平分线上？若存在，求出t的值；若不存在，请说明理由.

查看试题解析