浙江省杭州市萧山区六校2020-2021学年八年级下学期期中数学试卷

试卷更新日期：2022-03-17 类型：期中考试

进入出卷网下载

一、单选题

1. 下列二次根式中，不能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{8}$ C、 $\sqrt{18}$ D、 $\sqrt{12}$

查看试题解析
2. 已知x=﹣2是方程x²﹣4x+c=0的一个根，则c的值是（）

A、﹣12 B、﹣4 C、4 D、12

查看试题解析
3. 下列图形中，是中心对称图形的是（）

A、等腰三角形 B、直角三角形 C、等边三角形 D、平行四边形

查看试题解析
4. 解方程 $x^{2} - \sqrt{2} x = 0$ ，较简便的解法是（）

A、直接开平方法 B、配方法 C、公式法 D、因式分解法

查看试题解析
5. 一组数据 1，2，3，4，5 的方差与下列哪组数据的方差相同的是（）

A、2，4，6，8，10 B、10，20，30，40，50 C、11，12，13，14，15 D、11，22，33，44，55

查看试题解析
6. 已知实数 $x$ ， $y$ 满足 $y = 4 + \sqrt{5 - x} + \sqrt{x - 5}$ ，则 $| y - x |$ 的值是（）

A、1 B、4 C、5 D、9

查看试题解析
7. 已知m＝ $\sqrt{2 \times 8}$ + $\sqrt{5}$ ，则（）

A、4＜m＜5 B、5＜m＜6 C、6＜m＜7 D、7＜m＜8

查看试题解析
8. 如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，E，F，G，H，分别是AB，AC，CD，BD的中点，则四边形EFGH的周长是（）

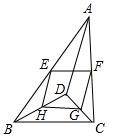A、7 B、9 C、10 D、11

查看试题解析
9. 已知关于x的一元二次方程（x﹣x₁）（x﹣x₂）＝0与一元一次方程2x﹣4＝0有一个公共解x＝x₁ ，若一元二次方程（x﹣x₁）（x﹣x₂）＋（2x﹣4）＝0有两个相等的实根，则x₂＝（）

A、﹣2 B、﹣4 C、2 D、4

查看试题解析
10. 已知▱ABCD中，AD＝2AB，F是BC的中点，作AE⊥CD，垂足E在线段CD上，不与点C重合，连接EF、AF，下列结论：①2∠BAF＝∠BAD；②EF＝AF；③S_△ABF≤S_△AEF；④∠BFE＝3∠CEF.中一定成立的是（）

A、①②④ B、①③ C、②③④ D、①②③④

查看试题解析

二、填空题

11. 已知一个多边形的内角和为540°，则这个多边形是边形．

查看试题解析
12. 用反证法证明命题“三角形中至少有两个锐角”，第一步应假设.

查看试题解析
13. 如图，有一块长 $21 m ，$ 宽 $10 m$ 的矩形空地，计划在这块空地上修建两块相同的矩形绿地，两块绿地之间及周边留有宽度相同的人行通道，两块绿地的面积和为 $90 m^{2}$ .设人行通道的宽度为 $x m$ ，根据题意可列方程：.

查看试题解析
14. 小方的数学平时成绩为84分，期中成绩为80分，学校按平时、期中、期末成绩之比为3∶3∶4的比例计算学期的总评成绩，他计划总评成绩要达到85分，则期末考试他至少要得到分.

查看试题解析
15. 在□ABCD中，AD=BD，BE是AD边上的高，∠EBD=28°，则∠A的度数为.

查看试题解析
16. 对于一元二次方程ax²+bx+c=0（a≠0），下列说法：①a+c=0，方程ax²+bx+c=0，有两个不相等的实数；②若方程ax²+bx+c=0有两个不相等的实根.则方程cx²+bx+a=0也一定有两个不相等的实根；③若c是方程ax²+bx+c=0的一个根，则一定有ac+b+1=0成立；④若m是方程ax²+bx+c=0的一个根，则一定有b²-4ac=（2am+b）²成立，其中正确的结论是.（把你认为正确结论的序号都填上）

查看试题解析

三、解答题

17. 计算：

(1)、 $3 \sqrt{3} - (\sqrt{12} + \sqrt{\frac{1}{3}})$ ；

(2)、 $(\sqrt{3} + \sqrt{2} + 1) (\sqrt{3} - \sqrt{2} + 1)$ .

查看试题解析
18. 用适当的方法解下列方程：

(1)、 $(x - 1)^{2} = 4$ ；

(2)、 $x (3 x - 6) = (x - 2)^{2}$

查看试题解析
19. 学校抽查了某班级某月份其中5天的用电量，数据如表（单位：度）：
度数
9
11
12
天数
3
1
1

(1)、求这5天用电量的平均数，众数，中位数.

(2)、学校共有48个班级，若该月在校时间按22天计，试估计该校该月的总用电量.

查看试题解析
20. 已知m，n是实数，定义运算“*”为：m*n＝mn+n．

(1)、分别求4*（﹣2）与4* $\sqrt{5}$ 的值；

(2)、若关于x的方程x*（a*x）＝﹣ $\frac{1}{4}$ 有两个相等的实数根，求实数a的值．

查看试题解析
21. 如图，在平行四边形ABCD中，∠ABC，∠BCD的平分线分别交AD于点E，F，BE，CF相交于点G.

(1)、求证：BE⊥CF；

(2)、求证：AF＝DE.

查看试题解析
22. 某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“五一”国际劳动节，商店决定采取适当的降价措施，以扩大销售量，尽快减少库存，增加利润.经市场调查发现，如果每件童装降价1元，那么平均可多售出2件.

(1)、设每件童装降价x元时，每天可销售件，每件盈利元；（用x的代数式表示）

(2)、为了扩大销售量，尽快减少库存，每件童装降价多少元时，平均每天赢利1200元；

(3)、平均每天赢利1200元是最大日赢利吗？如果是，请说明理由；如果不是，请求出平均日赢利的最大值.

查看试题解析
23. 如图，在四边形ABCD中，AD∥BC，∠B＝90°，AD＝16cm，AB＝12cm，BC＝21cm，动点P从点B出发，沿射线BC的方向以每秒2cm的速度运动到C点返回，动点Q从点A出发，在线段AD上以每秒1cm的速度向点D运动，点P，Q分别从点B，A同时出发，当点Q运动到点D时，点P随之停止运动，设运动的时间为t（秒）.

(1)、当t为何值时，四边形PQDC是平行四边形；

(2)、当t为何值时，以C，D，Q，P为顶点的四边形面积等于60cm²？

(3)、当0<t<10.5时，是否存在点P，使△PQD是等腰三角形？若存在，请直接写出所有满足要求的t的值；若不存在，请说明理由.

查看试题解析

度数	9	11	12
天数	3	1	1