浙江省杭州市十三中教育集团（总校）2020-2021学年八年级下学期期中数学试卷

试卷更新日期：2022-03-17 类型：期中考试

进入出卷网下载

一、单选题

1. 下列几何图形是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若代数式 $\sqrt{2 x - 4}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥2 B、x≠2 C、x>2
D：x≤2

查看试题解析
3. 小明家1至6月份的用水量统计如图所示，关于这组数据，下列说法中正确的是（）

A、平均数为 $4.5$ ，众数是 $6$ B、平均数为 $5$ ，众数是 $6$ C、平均数为 $4.5$ ，众数是 $5$ D、平均数为 $5$ ，众数是 $5$

查看试题解析
4. 下列各式中正确的是（）

A、 $\sqrt{16} = \pm 4$ B、 $\sqrt{8} = 4$ C、 $\sqrt{{(- 4)}^{2}} = - 4$ D、 $(- \sqrt{7})^{2} = 7$

查看试题解析
5. 下列条件不能判定四边形 $A B C D$ 是平行四边形的是（）.

A、 $A D = B C$ ， $A B = C D$ B、 $∠ A = ∠ C$ ， $∠ B = ∠ D$ C、 $A B / / C D$ ， $B C = A D$ D、 $A D / / B C$ ， $∠ B = ∠ D$

查看试题解析
6. 某快递公司今年一月份完成投递的快递总件数为10万件，二月份、三月份每月投递的件数逐月增加，第一季度总投递件数为 $33.1$ 万件，问：二、三月份平均每月的增长率是多少？设平均每月增长的百分率为 $x$ ，根据题意得方程（）.

A、 $10 {(1 + x)}^{2} = 33.1$ B、 $10 (1 + x) + 10 {(1 + x)}^{2} = 33.1$ C、 $10 + 10 {(1 + x)}^{2} = 33.1$ D、 $10 + 10 (1 + x) + 10 {(1 + x)}^{2} = 33.1$

查看试题解析
7. 如图所示，在平行四边形 $A B C D$ 中， $A C$ 与 $B D$ 相交于点O，过点O作直线m交线段 $A B$ 于点E，交线段 $C D$ 于点F.则图中共有几对全等三角形（）

A、4 B、5 C、6 D、7

查看试题解析
8. 已知关于x的一元二次方程 $x^{2} + 4 x + m - 3 = 0$ 有两个负整数根，则符合条件的所有正整数m的和为（）

A、16 B、13 C、10 D、7

查看试题解析
9. 如图所示，以平行四边形 $A B C D$ 的边 $A B$ 为边向内作等边 $△ A B E$ ，使 $A D = A E$ ，且点E在平行四边形内部，连结 $D E ， C E$ ，则 $∠ C E D$ 的度数为（）

A、 $150 °$ B、 $145 °$ C、 $135 °$ D、 $120 °$

查看试题解析
10. 如图所示，点E为 $▱ A B C D$ 内一点，连结 $E A ， E B ， E C ， E D ， A C$ ，已知 $△ B C E$ 的面积为2， $△ C E D$ 的面积为10，则阴影部分 $△ A C E$ 的面积为（）

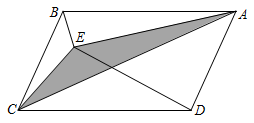A、5 B、6 C、7 D、8

查看试题解析

二、填空题

11. 化简： $\sqrt{\frac{1}{3}} =$ ； $\sqrt{(- 2)^{2}} =$ .

查看试题解析
12. 一个多边形的内角和为 $900 °$ ，则这个多边形是边形，它的外角和等于.

查看试题解析
13. 已知一组数据 $a_{1} ， a_{2} ， a_{3} ， a_{4} ， a_{5}$ 的方差是 $S_{1}$ ，另一组数据 $a_{1} - 6 ， a_{2} - 6 ， a_{3} - 6 ， a_{4} - 6 ， a_{5} - 6$ 的方差是 $S_{2}$ ，则 $S_{1}$ 与 $S_{2}$ 的大小关系是 $S_{1}$ $S_{2}$ （填写“＞”､“＜”或“－”）.

查看试题解析
14. 已知关于 $x$ 的方程 $(a - 1) x^{2} - 2 x + 1 = 0$ 有两个实数根，则 $a$ 的取值范围是.

查看试题解析
15. 如图，在平行四边形 $A B C D$ 中， $A C ， B D$ 相交于点O，点E，F在对角线 $B D$ 上，有下列条件：① $B F = D E$ ；② $A E = C F$ ；③ $∠ E A B = ∠ F C O$ ；④ $A F / / C E$ .其中一定能判定四边形 $A E C F$ 是平行四边形的是.

查看试题解析
16. 如图所示，在平行四边形 $A B C D$ 中，点E在线段 $B C$ 上且 $B E = 2 C E$ ，点F是 $C D$ 边的中点，若 $A E = 4 \sqrt{2}$ ， $A F = 4$ ，且 $∠ E A F = 45 °$ ，则 $A B$ 的长是.

查看试题解析

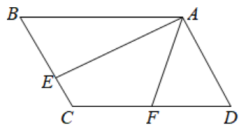
三、解答题

17. 计算：

(1)、 $2 \sqrt{5} \times \sqrt{10} \div {(\sqrt{2})}^{2}$

(2)、 ${(\sqrt{3} - 2)}^{2} + \sqrt{12}$

查看试题解析
18. 解一元二次方程：

(1)、 $2 x^{2} + 5 x - 3 = 0$

(2)、 ${(x - 3)}^{2} = 4 x - 12$

查看试题解析
19. 如图所示，在平行四边形 $A B C D$ 中，点E，点F分别是 $A D$ ､ $B C$ 的中点.连结 $B E$ ､ $D F$ .

(1)、求证：四边形 $B E D F$ 是平行四边形.

(2)、若 $B E$ 平分 $∠ A B C ， A B = 3$ ，求平行四边形 $A B C D$ 的周长.

查看试题解析
20. 张老师对李华和刘强两位同学从数学运算、逻辑推理、直观想象和数据分析四个方面考核他们的数学素养.单项检测成绩（百分制）列表如下：
姓名
数学运算
逻辑推理
直观想象
数据分析
李华
86
85
80
85
刘强
74
87
87
84

(1)、分别对两人的检测成绩进行数据计算，补全下表：
姓名
平均分
中位数
众数
方差
李华
84
85
85
刘强
83
87
$22.8$

(2)、你认为李华和刘强谁的数学素养更好？结合数据，从两个角度进行分析.

(3)、若将数学运算、逻辑推理、直观想象、数据分析四个检测成绩分别按权重30％，40％，20％，10％的比例计算最终考核得分，请分别计算李华和刘强的最终得分.

查看试题解析
21. 如图所示，某品牌 $1 L$ 的牛奶包装盒，高 $25 c m$ ，底面为长方形，将包装剪开铺平，得到如图的纸样.

(1)、牛奶包装盒底面长方形的长和宽分别是多少？

(2)、若不改变牛奶盒的容积和高度，将生奶盒的底面改为正方形，能否节约包装盒的纸张面积？若能，请计算每个生奶盒可节约的纸张面积；若不能，请说明理由.

查看试题解析
22. 已知关于x的一元二次方程 $x^{2} - (2 m + 4) x + m^{2} + 4 m = 0$ .

(1)、求证：无论m取何值，此方程总有两个不相等的实数根.

(2)、设方程的两个实数根分别为 $x_{1} ， x_{2}$ ，
①求代数式 ${x_{1}}^{2} + {x_{2}}^{2} - 4 x_{1} x_{2}$ 的最大值；
②若方程的一个根是6， $x_{1}$ 和 $x_{2}$ 是一个等腰三角形的两条边，求等腰三角形的周长.

查看试题解析
23. 如图所示， $△ A B C$ 是一个边长为4的等边三角形，D是直线 $B C$ 边上一点，以 $A D$ 为边作 $△ A D E$ ，使 $A E = A D ， ∠ D A E = 120 °$ ，并以 $A B$ ， $A E$ 为边作平行四边形 $A B F E$ .

(1)、当点D在线段 $B C$ 上时， $A D$ 交 $B F$ 于点G，求证： $△ A B D ≌ △ B C F$ ；

(2)、求线段 $B F$ 的最小值；

(3)、当直线 $A E$ 与 $△ A B C$ 的一边垂直时，请直接写出平行四边形 $A B F E$ 的面积.

查看试题解析

姓名	数学运算	逻辑推理	直观想象	数据分析
李华	86	85	80	85
刘强	74	87	87	84

姓名	平均分	中位数	众数	方差
李华	84	85	85
刘强	83		87	$22.8$