浙江省金华市义乌市2021-2022学年八年级上学期期末数学试卷
试卷更新日期:2022-03-17 类型:期末考试
一、单选题
-
1. 点P(−5,3)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 如图,已知图形X和直线l,以直线l为对称轴,图形X的轴对称图形是( )
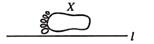 A、
A、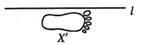 B、
B、 C、
C、 D、
D、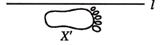 3. 一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )
3. 一个不等式的解集在数轴上表示如图所示,则这个不等式可能是( )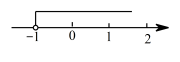 A、 B、 C、 D、4. 如图给出的三角形有一部分被遮挡,则这个三角形可能是( )
A、 B、 C、 D、4. 如图给出的三角形有一部分被遮挡,则这个三角形可能是( ) A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形5. 是不等式的一个解,则的值不可能是( )A、1 B、2 C、3 D、46. 下列叙述有误的是( )A、三角形任何两边的和大于第三边 B、对称轴一定垂直平分连结两个对称点的线段 C、所有的等边三角形都是全等图形 D、物体在平面上的位置可以用第几行第几列来确定,也可以用方向和距离来确定7. 在正比例函数y=kx中,y的值随着x值的增大而减小,则一次函数y=kx+k在平面直角坐标系中的图象大致是( )A、
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形5. 是不等式的一个解,则的值不可能是( )A、1 B、2 C、3 D、46. 下列叙述有误的是( )A、三角形任何两边的和大于第三边 B、对称轴一定垂直平分连结两个对称点的线段 C、所有的等边三角形都是全等图形 D、物体在平面上的位置可以用第几行第几列来确定,也可以用方向和距离来确定7. 在正比例函数y=kx中,y的值随着x值的增大而减小,则一次函数y=kx+k在平面直角坐标系中的图象大致是( )A、 B、
B、 C、
C、 D、
D、 8. 如图,在△DEC和△BFA中,点A,E,F,C在同一直线上,已知AB∥CD,且AB=CD,若利用“ASA”证明△DEC≌△BFA,则需添加的条件是( )
8. 如图,在△DEC和△BFA中,点A,E,F,C在同一直线上,已知AB∥CD,且AB=CD,若利用“ASA”证明△DEC≌△BFA,则需添加的条件是( ) A、EC=FA B、∠A=∠C C、∠D=∠B D、BF=DE9. 如图,是等腰三角形, , , BP平分;点D是射线BP上一点,如果点D满足是等腰三角形,那么的度数是( ).
A、EC=FA B、∠A=∠C C、∠D=∠B D、BF=DE9. 如图,是等腰三角形, , , BP平分;点D是射线BP上一点,如果点D满足是等腰三角形,那么的度数是( ). A、20°或70° B、20°、70°或100° C、40°或100° D、40°、70°或100°10. 如图,已知长方形纸板的边长 , , 在纸板内部画 , 并分别以三边为边长向外作正方形,当边、和点K、J都恰好在长方形纸板的边上时,则的面积为( )
A、20°或70° B、20°、70°或100° C、40°或100° D、40°、70°或100°10. 如图,已知长方形纸板的边长 , , 在纸板内部画 , 并分别以三边为边长向外作正方形,当边、和点K、J都恰好在长方形纸板的边上时,则的面积为( ) A、6 B、 C、 D、
A、6 B、 C、 D、二、填空题
-
11. 已知如图,有条对称轴.
 12. 请选择你认为合适的不等号填入:0,0.13. 根据图中所给信息,写出一个真命题:.
12. 请选择你认为合适的不等号填入:0,0.13. 根据图中所给信息,写出一个真命题:. 14. △ABC为等腰三角形,周长为7cm,且各边长为整数,则该三角形最长边的长为cm.15. 某产品进价为每件200元,商店标价为每件300元.现商店准备将这批服装打折出售,但要保证毛利润不低于5%,则商店最低可按折出售.16. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,1)、B(3,1)、C(2,2),线段DE在y轴上,坐标分别为(0,−1)、(0,−3),直线y=kx+b与线段DE交于点P.
14. △ABC为等腰三角形,周长为7cm,且各边长为整数,则该三角形最长边的长为cm.15. 某产品进价为每件200元,商店标价为每件300元.现商店准备将这批服装打折出售,但要保证毛利润不低于5%,则商店最低可按折出售.16. 如图,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,1)、B(3,1)、C(2,2),线段DE在y轴上,坐标分别为(0,−1)、(0,−3),直线y=kx+b与线段DE交于点P. (1)、当点P与点D重合时,直线y=kx+b与△ABC有交点,则k的取值范围是.(2)、当点P是线段DE上任意一点时,直线y=kx+b与△ABC有交点,则k的取值范围是.
(1)、当点P与点D重合时,直线y=kx+b与△ABC有交点,则k的取值范围是.(2)、当点P是线段DE上任意一点时,直线y=kx+b与△ABC有交点,则k的取值范围是.三、解答题
-
17. 解不等式组.18. 如图,在每个小正方形的边长为1个单位的网格中建立平面直角坐标系,已知线段的两个端点均在格点(网格线的交点)上,且 , .
 (1)、将线段向上平移2个单位,再向右平移5个单位得到线段 , 画出线段(点 , 分别为A,B的对应点);(2)、若点为线段上任意一点,经过(1)的平移后,在线段上对应的点的坐标为.19. 如图,已知一次函数 , 与x轴的交点横坐标分别为6和 , 、的交点P(3,n).
(1)、将线段向上平移2个单位,再向右平移5个单位得到线段 , 画出线段(点 , 分别为A,B的对应点);(2)、若点为线段上任意一点,经过(1)的平移后,在线段上对应的点的坐标为.19. 如图,已知一次函数 , 与x轴的交点横坐标分别为6和 , 、的交点P(3,n). (1)、求、的函数解析式;(2)、x取何值时,函数的图象在函数图象的上方?20. 如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且BE=BF.
(1)、求、的函数解析式;(2)、x取何值时,函数的图象在函数图象的上方?20. 如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且BE=BF. (1)、求证:△ABE≌△CBF;(2)、若∠CAE=30°,求∠ACF的度数.21. 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,那么当成人按规定量服药后,根据图象回答下列问题:
(1)、求证:△ABE≌△CBF;(2)、若∠CAE=30°,求∠ACF的度数.21. 某医药研究所开发了一种新药,在实验药效时发现,如果成人按规定剂量服用,每毫升血液中含药量y(微克)随时间x(时)的变化情况如图所示,那么当成人按规定量服药后,根据图象回答下列问题: (1)、服药小时,血液中含药量最高,达到每毫升微克,接着逐步衰减.服药后5小时,血液中含药量每毫升微克.(2)、如果每毫升血液中含药量为3微克及以上时治疗疾病有效.某老师要在上午8:00~11:30之间参加活动,则该老师在哪个时间段内服药,才能使药效持续有效?请你通过计算说明.22. 12月,浙江突发疫情,我市立即启动疫情应急处置模拟演练.为配合演练顺利开展,某校需要购进A、B两款体温枪共100只.已知购进A型体温枪花费1000元,B型体温枪花费1500元,A型体温枪的价格比B型高50元,B型体温枪的数量是A型的两倍.(1)、求每只A型、B型体温枪的价格;(2)、若购进B型体温枪的数量不超过A型体温枪的2倍,设购进A型体温枪x只,这100只体温枪的总费用为y元.
(1)、服药小时,血液中含药量最高,达到每毫升微克,接着逐步衰减.服药后5小时,血液中含药量每毫升微克.(2)、如果每毫升血液中含药量为3微克及以上时治疗疾病有效.某老师要在上午8:00~11:30之间参加活动,则该老师在哪个时间段内服药,才能使药效持续有效?请你通过计算说明.22. 12月,浙江突发疫情,我市立即启动疫情应急处置模拟演练.为配合演练顺利开展,某校需要购进A、B两款体温枪共100只.已知购进A型体温枪花费1000元,B型体温枪花费1500元,A型体温枪的价格比B型高50元,B型体温枪的数量是A型的两倍.(1)、求每只A型、B型体温枪的价格;(2)、若购进B型体温枪的数量不超过A型体温枪的2倍,设购进A型体温枪x只,这100只体温枪的总费用为y元.①求y关于x的函数关系式;
②某校实际购买时,发现某店对A型体温枪进行降价处理,比原价降低a元出售( , 且a为正整数),且限定一次性最多购买A型体温枪50只,当a满足什么条件时,能使该校购进这100只体温枪总费用最小.
23. 如图,长方形 , 点E是上的一点,将沿折叠后得到 , 且点O在长方形内部.已知 , . (1)、如图1,若 , 求四边形的面积.(2)、如图2,延长交于F,连结 , 将沿折叠,当点D的对称点恰好为点O时,求四边形的面积.(3)、如图3,在(2)的条件下,延长交于点G,连结 , 将沿折叠,当点C的对称点恰好为点O时,求四边形的面积.24. 如图,已知为等腰直角三角形,且面积为4.点D是的中点,点F是直线上一动点,连结.
(1)、如图1,若 , 求四边形的面积.(2)、如图2,延长交于F,连结 , 将沿折叠,当点D的对称点恰好为点O时,求四边形的面积.(3)、如图3,在(2)的条件下,延长交于点G,连结 , 将沿折叠,当点C的对称点恰好为点O时,求四边形的面积.24. 如图,已知为等腰直角三角形,且面积为4.点D是的中点,点F是直线上一动点,连结. (1)、求线段的长;(2)、当点E在射线上,且时,连结 , 若 , 试判断是否为等腰三角形,并说明理由;(3)、直线上是否存在点F(F不与重合),使的其中两边之比为?若存在,求出的长;若不存在,请说明理由.
(1)、求线段的长;(2)、当点E在射线上,且时,连结 , 若 , 试判断是否为等腰三角形,并说明理由;(3)、直线上是否存在点F(F不与重合),使的其中两边之比为?若存在,求出的长;若不存在,请说明理由.