广西壮族自治区防城港市上思县2021-2022学年八年级上学期期末数学试卷

试卷更新日期：2022-03-17 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 要使分式 1x−1 有意义，则x的取值范围是（   ）
    A、x=1 B、x≠1 C、x=−1 D、x≠−1

    查看试题解析

  • 2. 下面四个图形分别是节能、节水、低碳和绿色食品标志，在这四个标志中，是轴对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

  • 3. 在平面直角坐标系中，点（2，3）关于x轴对称的点的坐标是（   ）
    A、（-2，-3） B、（-2，3） C、（2，-3） D、（3，2）

    查看试题解析

  • 4. 如图，为估计池塘岸边A、B两点的距离，小方在池塘的一侧选取一点O，OA=15米，OB＝10米，A、B间的距离不可能是（  ）

    A、5米 B、10米 C、15米 D、20米

    查看试题解析

  • 5. 下列图形中，正确画出AC边上的高的是（     ）
    A、 B、 C、 D、

    查看试题解析

  • 6. 下列计算中，正确的是（   ）
    A、（2a）3=2a3 B、a3+a2=a5 C、a8÷a4=a2 D、（a2）3=a6

    查看试题解析

  • 7.

    如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（　　）


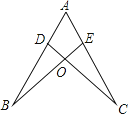    A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD

    查看试题解析

  • 8. 分解因式a2b﹣b3结果正确的是（   ）
    A、b（a+b）（a﹣b） B、b（a﹣b）2 C、b（a2﹣b2） D、b（a2+b2）

    查看试题解析

  • 9. 如图，在△ABC中，AC的垂直平分线分别交AC、BC于E，D两点，EC＝4，△ABC的周长为23，则△ABD的周长为（  ）

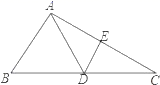    A、13 B、15 C、17 D、19

    查看试题解析

  • 10. 若（x﹣2）（x+3）=x2+ax+b，则a，b的值分别为（   ）
    A、a=5，b=﹣6 B、a=5，b=6 C、a=1，b=6 D、a=1，b=﹣6

    查看试题解析

  • 11. 如图，小明从A点出发前进10m，向右转15°，再前进10m，又向右转15°，…，这样一直走下去，他第一次回到出发点A时，一共走了（   ）

    A、240m B、230m C、220m D、200m

    查看试题解析

  • 12. 如图，在等腰△ABC中，AB=AC ， ∠BAC=50° ， ∠BAC的平分线与AB的垂直平分线交于点E，沿FG折叠使点C与点E重合，则∠CFG的度数是（ ）.

    A、60度 B、55° C、50° D、45°

    查看试题解析

二、填空题

三、解答题

  • 19. 化简：
    (1)、化简：x3y﹣4x2y+4xy；
    (2)、化简：（x﹣3y）2+3y（2x﹣3y）.

    查看试题解析

  • 20.

    如图，在平面直角坐标系中，△ABC的顶点A（0，1），B（3，2），C（1，4）均在正方形网格的格点上．

    (1)、画出△ABC关于x轴的对称图形△A1B1C1；

    (2)、将△A1B1C1向左平移3个单位后得到△A2B2C2 ， 画出△A2B2C2 ， 并写出顶点A2的坐标．

    查看试题解析

  • 21. 先化简，再求值： x+1x ÷（x+ 2x+1x ），其中x=﹣3．

    查看试题解析

  • 22. 如图，已知点B、E、C、F在一条直线上，AC∥DE，AC＝DE，∠A＝∠D.

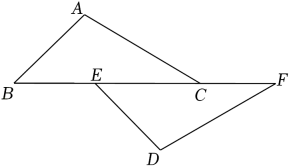    (1)、求证：AB＝DE；
    (2)、若BC＝9，EC＝5，求BF的长.

    查看试题解析

  • 23. 如图，图1为边长为a的大正方形中有一个边长为b的小正方形，图2是由图1中阴影部分拼成的一个长方形.

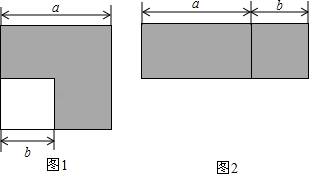    (1)、设图1中阴影部分面积为S1 ， 图2中阴影部分面积为S2 ， 请用含a、b的代数式表示：S1＝ ， S2＝（只需表示，不必化简）；
    (2)、以上结果可以验证哪个乘法公式？请写出这个乘法公式 ；
    (3)、运用（2）中得到的公式，计算：20152﹣2016×2014.

    查看试题解析

  • 24. 如图，在△ABC中，AB=AC．

    (1)、尺规作图：作∠ABC的平分线，交AC于点D（保留作图痕迹，不写作法）；
    (2)、E是底边BC的延长线上一点，M是BE的中点，连接DE、DM．若CE=CD，求证：DM⊥BE．

    查看试题解析

  • 25. 为改善南宁市的交通现状，市政府决定修建地铁，甲、乙两工程队承包地铁1号线的某段修建工作，从投标书中得知：甲队单独完成这项工程所需天数是乙队单独完成这项工程所需天数的3倍；若由甲队先做20天，剩下的工程再由甲、乙两队合作10天完成．
    (1)、求甲、乙两队单独完成这项工程各需多少天？
    (2)、已知甲队每天的施工费用为15.6万元，乙队每天的施工费用为18.4万元，工程预算的施工费用为500万元，为缩短工期，拟安排甲、乙两队同时开工合作完成这项工程，那么工程预算的施工费用是否够用？若不够用，需增加多少万元？

    查看试题解析

  • 26.

    如图，边长为4cm的等边△ABC中，点P、Q分别是边AB、BC上的动点（端点除外），点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，连接AQ，CP交于点M，在点P，Q运动的过程中．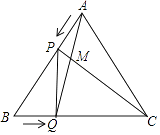

    (1)、求证：△ABQ≌△CAP；

    (2)、∠QMC的大小是否发生变化？若无变化，求∠QMC的度数；若有变化，请说明理由；

    (3)、连接PQ，当点P，Q运动多少秒时，△PBQ是直角三角形？

    查看试题解析