浙江省金华市金东区2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-03-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件中，是必然事件的是（）

A、购买一张彩票，中奖 B、射击运动员射击一次，命中靶心 C、经过有交通信号灯的路口，遇到红灯 D、任意画一个三角形，其内角和是180°

查看试题解析
2. 经过圆锥顶点的截面的形状可能是（）

A、 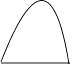B、 C、 D、

查看试题解析
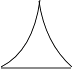3. 若⊙O的半径为5cm，点A到圆心O的距离为4cm，那么点A与⊙O的位置关系是（）

A、点A在圆外 B、点A在圆上 C、点A在圆内 D、不能确定

查看试题解析
4. 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上，点A，B的度数分别为86°和30°，则∠ACB的度数为（）

A、28° B、30° C、43° D、56°

查看试题解析
5.
如图，一个斜坡长130m，坡顶离水平地面的距离为50m，那么这个斜坡与水平地面夹角的正切值等于（）

A、 $\frac{5}{13}$ B、 $\frac{12}{13}$ C、 $\frac{5}{12}$ D、 $\frac{13}{12}$

查看试题解析
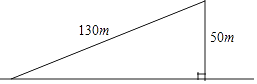6. 正方形外接圆的半径为2，则其内切圆的半径为（）

A、 $2 \sqrt{2}$ B、 $\sqrt{2}$ C、1 D、 $\frac{\sqrt{2}}{2}$

查看试题解析
7.
如图，AB是⊙O的弦，半径OA=2，sinA= $\frac{2}{3}$ ，则弦AB的长为( )

A、 $\frac{2 \sqrt{5}}{3}$ B、 $\frac{2 \sqrt{13}}{3}$ C、4 D、 $\frac{4 \sqrt{5}}{3}$

查看试题解析
8. 如图，将函数y＝ $\frac{1}{2}$ （x﹣2）²+1的图象沿y轴向上平移得到一条新函数的图象，其中点A（1，m），B（4，n）平移后的对应点分别为点A'、B'．若曲线段AB扫过的面积为9（图中的阴影部分），则新图象的函数表达式是（）

A、y＝ $\frac{1}{2}$ （x﹣2）²-2 B、y＝ $\frac{1}{2}$ （x﹣2）²+7 C、y＝ $\frac{1}{2}$ （x﹣2）²-5 D、y＝ $\frac{1}{2}$ （x﹣2）²+4

查看试题解析
9. 如图，在△ABC中，点D是AB边上的一点，若∠ACD=∠B，AD＝1，AC＝2，△ADC的面积为1，则△BCD的面积为（）

A、1 B、2 C、3 D、4

查看试题解析
10. 二次函数y=ax²+bx+c（a、b、c是常数，且a≠0）的图象如图所示，下列结论错误的是（）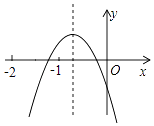

A、4ac＜b² B、abc＜0 C、b+c＞3a D、a＜b

查看试题解析

二、填空题

11. 若 $\frac{a}{b}$ ＝ $\frac{3}{4}$ ，则 $\frac{a + b}{b}$ ＝.

查看试题解析
12. 若二次函数 $y = x^{2} - 4 x + n$ 的图象与x轴只有一个公共点，则实数n=.

查看试题解析
13. 在圆内接四边形ABCD中， $∠ D - ∠ B = 40 °$ ，则 $∠ D$ 的度数为.

查看试题解析
14. 一个圆柱的底面直径为20，母线长为15，则这个圆柱的侧面积为.

查看试题解析
15. 在如图的正方形方格纸中，每个小的四边形都是相同的正方形，A，B，C，D都在格点处，AB与CD相交于O，则 $t a n ∠ A O C$ 的值.

查看试题解析
16. 如图，已知正方形ABCD的边长为4，点E在BC上，DE为以AB为直径的半圆的切线，切点为F，连结CF，则ED的长为， CF的长为.

查看试题解析

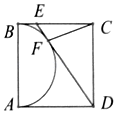
三、解答题

17. 计算：sin30°•tan45°+sin²60°﹣2cos60°.

查看试题解析
18. 已知抛物线 $y = x^{2} + b x - 3$ （b是常数）经过点 $A (- 1 ， 0)$ .求该抛物线的解析式和顶点坐标.

查看试题解析
19. 如图，已知AB是 $⊙ O$ 的直径，点D为弦BC中点，过点C作 $⊙ O$ 切线，交OD延长线于点E，连结BE，OC.

(1)、求证：EC＝EB.

(2)、求证：BE是⊙O的切线.

查看试题解析
20. 如图，一条公路的转弯处是一段圆弧 $(\overset{⌢}{A B}) .$

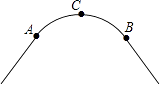(1)、用直尺和圆规作出 $\overset{⌢}{A B}$ 所在圆的圆心O； $($ 要求保留作图痕迹，不写作法 $)$

(2)、若 $\overset{⌢}{A B}$ 的中点C到弦AB的距离为 $20 m ， A B = 80 m$ ，求 $\overset{⌢}{A B}$ 所在圆的半径．

查看试题解析

21. 在同样的条件下对某种小麦种子进行发芽试验，统计发芽种子数，获得如下频数表.

实验种子数（粒）	1	5	50	100	200	500	1000	2000	3000
发芽频数	0	4	45	92	188	476	951	1900	2850

(1)、估计该麦种的发芽概率.

(2)、如果播种该种小麦每公顷所需麦苗数为4000000棵，种子发芽后的成秧率为80%，该麦种的千粒质量为50g.那么播种3公顷该种小麦，估计约需麦种多少千克（精确到1kg）？

查看试题解析

22. 已知如图，点C在线段AB上，过点B作直线 $l ⊥ A B$ ，点P为直线l上的一点，连结AP，点Q为AP中点，作 $Q R ⊥ A B$ ，垂足为R，连结CQ， $A C = 2$ ， $B C = 1$ ， $C Q = 1$ .

(1)、求CR的长.

(2)、求证：△RCQ∽△QCA.

(3)、求∠AQC的度数.

查看试题解析
23. 如图，已知AB是圆O直径，过圆上点C作 $C D ⊥ A B$ ，垂足为点D.连结OC，过点B作 $B E ∥ O C$ ，交圆O于点E，连结AE，CE， $B D = 1$ ， $A B = 6$ .

(1)、求证：△CDO∽△AEB.

(2)、求sin∠ABE的值.

(3)、求CE的长.

查看试题解析
24. 已知抛物线 $y = \frac{1}{m} (x + 2) (x - m)$ 与x轴负半轴交于点A，与x轴正半轴交于点B，与y轴交于点C，点P为抛物线上一动点（点P不与点C重合）.

(1)、当△ABC为直角三角形时，求△ABC的面积.

(2)、如图，当AP $∥$ BC时，过点P作PQ⊥x轴于点Q，求BQ的长；

(3)、当以点A，B，P为顶点的三角形和△ABC相似时（不包括两个三角形全等），求m的值.

查看试题解析