浙江省绍兴市诸暨市2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-03-17 类型：期末考试

进入出卷网下载

一、单选题

1. 已知实数a，b满足 $a = 2 b$ ，则 $\frac{a}{b}$ 的值是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、1 D、2

查看试题解析
2. 已知点P到圆心O的距离为5，若点P在圆内，则 $⊙ O$ 的半径可能为（）

A、3 B、4 C、5 D、6

查看试题解析
3. 如图，四边形ABCD是 $⊙ O$ 的内接四边形，其中 $∠ A = 100 °$ ，则 $∠ C$ 的度数为（）

A、130° B、100° C、80° D、50°

查看试题解析
4. “对于二次函数 $y = {(x - 1)}^{2} + 1$ ，当 $x \geq 1$ 时，y随x的增大而增大”，这一事件为（）

A、必然事件 B、随机事件 C、不确定事件 D、不可能事件

查看试题解析
5. 如图，AB∥CD，AB=2，CD=3，AD=4，则OD的长为（）

A、 $\frac{8}{3}$ B、 $\frac{8}{5}$ C、 $\frac{12}{7}$ D、 $\frac{12}{5}$

查看试题解析
6. 如图，是一个圆形人工湖，弦AB是湖上的一座桥.已知AB的长为10，圆周角 $∠ C = 30 °$ ，则弧AB的长为（）

A、 $\frac{5}{3} π$ B、 $\frac{10}{3} π$ C、 $\frac{15}{3} π$ D、 $\frac{20}{3} π$

查看试题解析
7. 如图， $△ A B C$ 的顶点均在正方形网格的格点上，则 $s i n ∠ A B C$ 的值为（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
8. 如图，小聪和他同学利用影长测量旗杆的高度，当1米长的直立的竹竿的影长为1.5米时，此时测得旗杆落在地上的影长为12米，落在墙上的影长为2米，则旗杆的实际高度为（）

A、8米 B、10米 C、18米 D、20米

查看试题解析
9. 如图，图1是装了液体的高脚杯，加入一些液体后如图2所示，则此时液面AB为（）

A、5.6cm B、6.4cm C、8cm D、10cm

查看试题解析
10. 如图，△ABC为锐角三角形，BC=6，∠A=45°，点O为△ABC的重心，D为BC中点，若固定边BC，使顶点A在△ABC所在平面内进行运动，在运动过程中，保持∠A的大小不变，则线段OD的长度的取值范围为（）

A、 $\sqrt{5} < O D \leq \sqrt{2} + 1$ B、 $\sqrt{5} < O D \leq \sqrt{3} + 1$ C、 $1 \leq O D < \sqrt{3} + 1$ D、 $1 < O D \leq \sqrt{2} + 1$

查看试题解析

二、填空题

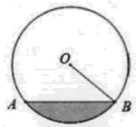
11. 在一个不透明的口袋中装有3个绿球、2个黑球和1个红球，它们除颜色外其余均相同，若从中随机摸出一个球，它是黑球的概率为.

查看试题解析
12. 已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 的对称轴为直线 $x = 2$ ，且与x轴有两个交点，其中一个交点坐标为 $(- 1 ， 0)$ ，则另一个交点坐标为.

查看试题解析
13. 一根排水管的截面如图所示，已知排水管的半径 $O B = 10$ ，水面宽 $A B = 12$ ，如果再注入一些水，当水面AB的宽变为16时，则水面AB上升的高度为.

查看试题解析
14. 如图，扇形AOB，正方形OCDE的顶点C，E，D，分别在OA，OB，弧AB上，过点A作 $A F ⊥ E D$ ，交ED的延长线于点F.若图中阴影部分的面积为 $\sqrt{2} - 1$ ，则扇形AOB的半径为.

查看试题解析
15. 如图1，以 $R t △ A B C$ 各边为边分别向外作等边三角形，编号为①、②、③，将②、①如图2所示依次叠在③上，已知四边形EMNB与四边形MPQN的面积分别为 $9 \sqrt{3}$ 与 $7 \sqrt{3}$ ，则 $R t △ A B C$ 的斜边长 $A B =$ .

查看试题解析
16. 已知点 $A (0 ， 0)$ ， $B (4 ， 0)$ ， $C (- 1 ， - 1)$ ， $D (2 ， - 4)$ ，固定A，B两点，将线段CD向左或向右平移，平移后C，D两点的对应点分别为 $C_{1}$ ， $D_{1}$ .

(1)、当 $C_{1}$ 的坐标为 $(- 2 ， - 1)$ 时，四边形 $A C_{1} D_{1} B$ 的周长为.

(2)、当 $C_{1}$ 的坐标为时，四边形 $A C_{1} D_{1} B$ 的周长最小.

查看试题解析

三、解答题

17. 计算： $\sqrt{3} t a n 30 ° \cdot c o s 60 ° - s i n^{2} 45 ° + {(π + 2022)}^{0}$

查看试题解析
18. 在平面直角坐标系中，已知抛物线 $C ： y = - x^{2} + b x + c$ 经过点 $(0 ， 3)$ 和 $(1 ， 1)$ .

(1)、求抛物线C的解析式；

(2)、将抛物线C先向左平移2个单位，再向下平移1个单位，得到抛物线 $C_{1}$ ，求抛物线 $C_{1}$ 的顶点坐标.

查看试题解析
19. 有一个转盘如图所示，让转盘自由转动.求：

(1)、转盘自由转动一次，指针落在黄色区域的概率；

(2)、转盘自由转动两次，请利用树状图或列表法求出指针一次落在黄色区域，另一次落在红色区域的概率.

查看试题解析
20. 为有效预防新型冠状病毒的传播，如图1为医院里常见的“测温门”，图2为该“测温门”截面示意图.小聪做了如下实验：当他在地面M处时“测温门”开始显示额头温度，此时在额头B处测得A的仰角为30°；当他在地面N处时，“测温门”停止显示额头温度，此时在额头C处测得A的仰角为60°.经测量该测温门的高度AD为2.5米，小聪的有效测温区间MN的长度是1米，根据以上数据，求小聪的身高CN为多少？（注：额头到地面的距离以身高计）（参考数据： $\sqrt{3} \approx 1.732$ ，结果精确到0.01米）

查看试题解析
21. 如图，O为半圆的圆心，C、D为半圆上的两点，连接CD、BD、AD， $C D = B D$ .连接AC并延长，与BD的延长线相交于点E.

(1)、求证： $C D = D E$ ；

(2)、若 $A C = 6$ ，半径 $O B = 5$ ，求BD的长.

查看试题解析
22. 山下湖是全国优质淡水珍珠的主产地，已知一批珍珠每颗的出厂价为30元，当售价定为50元/颗时，每天可销售60颗，为增大市场占有率，在保证盈利的情况下，商家决定采取降价措施，经调査发现，每颗售价降低1元，每天销量可增加10颗.

(1)、写出商家每天的利润W元与降价x元之间的函数关系；

(2)、当降价多少元时，商家每天的利润最大，最大为多少元？

(3)、若商家每天的利润至少要达到1440元，则定价应在什么范围内？

查看试题解析
23. 足球射门时，在不考虑其他因素的条件下，射点到球门AB的张角越大，射门越好.当张角达到最大值时，我们称该射点为最佳射门点.通过研究发现，如图1所示，运动员带球在直线CD上行进时，当存在一点Q，使得 $∠ C Q A = ∠ A B Q$ （此时也有 $∠ D Q B = ∠ Q A B$ ）时，恰好能使球门AB的张角 $∠ A Q B$ 达到最大值，故可以称点Q为直线CD上的最佳射门点.

(1)、如图2所示，AB为球门，当运动员带球沿CD行进时， $Q_{1}$ ， $Q_{2}$ ， $Q_{3}$ 为其中的三个射门点，则在这三个射门点中，最佳射门点为点；

(2)、如图3所示，是一个矩形形状的足球场，AB为球门， $C D ⊥ A B$ 于点D， $A B = 3 a$ ， $B D = a$ .某球员沿CD向球门AB进攻，设最佳射门点为点Q.
①用含a的代数式表示DQ的长度并求出 $t a n ∠ A Q B$ 的值；

②已知对方守门员伸开双臂后，可成功防守的范围为 $\frac{\sqrt{5}}{4} a$ ，若此时守门员站在张角 $∠ A Q B$ 内，双臂张开MN垂直于AQ进行防守，求MN中点与AB的距离至少为多少时才能确保防守成功.（结果用含a的代数式表示）

查看试题解析
24. 已知如图，在平面直角坐标系中，已知菱形OABC的边长为25，且 $t a n ∠ A O C = \frac{24}{7}$ .

(1)、求C、B两点的坐标；

(2)、设P为菱形OABC对角线OB上的一动点，连接CP.
①若 $∠ O C P = ∠ C O P$ ，求点P的坐标；
②已知点G在坐标平面内且在直线OC下方，若点P在运动过程中始终保持 $∠ C P G = ∠ C O B$ ，且 $C P = P G$ ，当 $△ O C P$ 为等腰三角形时，求AG的长度.

查看试题解析