浙江省绍兴市新昌县2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-03-17 类型：期末考试

进入出卷网下载

一、单选题

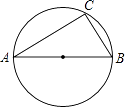
1. 成语“水中捞月”所描述的事件是（）.

A、必然事件 B、随机事件 C、不可能事件 D、无法确定

查看试题解析
2. 如图，已知AB是△ABC外接圆的直径，∠A=35°，则∠B的度数是（）

A、35° B、45° C、55° D、65°

查看试题解析
3. 抛物线 $y = 5 {(x + 1)}^{2} - 3$ 的顶点坐标为（）

A、 $(1 ， - 3)$ B、（1，3） C、 $(- 1 ， 3)$ D、 $(- 1 ， - 3)$

查看试题解析
4. 如图，在Rt△ABC中，∠C=90°， AC=3，BC=4，则sinA的值为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
5. 已知扇形的圆心角为120°，半径为3cm，则弧长为（）

A、 $\frac{2 π}{3} c m$ B、2πcm C、4cm D、 $\frac{π}{3} c m$

查看试题解析
6. 如图，在下列四个三角形中，与△ABC相似的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，AB是 $⊙ O$ 的弦，OC⊥AB于点C，连结OB，P是半径OB上任意一点，连结AP，若OB＝5，OC＝3，则AP的长不可能是（）.

A、6 B、7 C、8 D、9

查看试题解析
8. 如图，取一根等宽的纸条打个结再拉紧，重叠部分是正五边形，则FD：BF的值为（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{\sqrt{5} + 1}{2}$ C、0.618 D、 $\sqrt{5} - 1$

查看试题解析
9. 如图，圆的半径为4，则图中阴影部分的周长是（）

A、 $4 \sqrt{3}$ B、 $8 \sqrt{3}$ C、24 D、 $24 \sqrt{3}$

查看试题解析
10. 如图，在矩形ABCD中，AB＝8，BC＝6，顺次连结各边中点得到菱形，再顺次连结菱形各边中点，得到矩形 $A_{2} B_{2} C_{2} D_{2}$ ，再顺次连结矩形 $A_{2} B_{2} C_{2} D_{2}$ 各边中点，得到菱形 $A_{3} B_{3} C_{3} D_{3}$ ， …，这样继续下去.则四边形 $A_{2022} B_{2022} C_{2022} D_{2022}$ 的面积为（）

A、 $\frac{3}{2^{2017}}$ B、 $\frac{3}{2^{2018}}$ C、 $\frac{3}{2^{2019}}$ D、 $\frac{48}{2^{2021}}$

查看试题解析

二、填空题

11. 布袋中装有1个红球和2个白球，它们除颜色外其他都相同，如果从布袋里随机摸出一个球，那么所摸到的球恰好为红球的概率为.

查看试题解析
12. 如图，点A，B，C是 $⊙ O$ 上的三个点，∠C＝50°，则∠AOB＝.

查看试题解析
13. 将抛物线 $y = 2 x^{2}$ 向左平移 $\frac{1}{2}$ 个单位，再向下平移2个单位后，所得新抛物线的函数表达式是.

查看试题解析
14. 如图，在△ABC中，点D，E分别在AB，AC上，∠AED＝∠B， $A D = \frac{3}{4} A C$ ，若四边形BCED的面积为7，则△ADE的面积为.

查看试题解析
15. 某车在弯路上做刹车试验，收集到的数据如下表所示：
速度x（km/h）
0
5
10
15
20
a
…
刹车距离y（m）
0
0.75
2
3.75
6
12
…
则a＝km/h.

查看试题解析
16. 如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝6，BD＝2，以点B为圆心，BD长为半径作圆，点E为 $⊙ B$ 上的动点，连结EC，作FC⊥CE，垂足为C，点F在直线BC的上方，且满足 $C F = \frac{1}{2} C E$ ，连结BF.当点E与点D重合时，BF的值为.点E在 $⊙ B$ 上运动过程中，BF存在最大值为.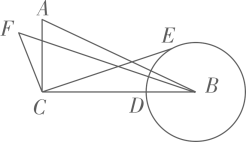

查看试题解析

三、解答题

17. 计算：

(1)、 $c o s 45 ° - 2 s i n 30 ° + t a n 60 °$ .

(2)、已知线段a＝4，b＝6，求线段a，b的比例中项c的长.

查看试题解析
18. 如图，在平面直角坐标系中有一个△ABO，其中点A，B的坐标分别为 $(- 4 ， 2)$ ， $(- 2 ， 4)$ .

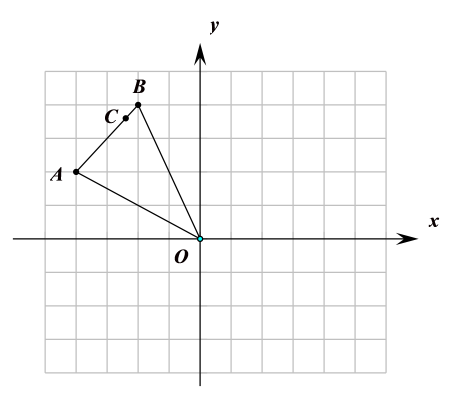(1)、以坐标原点O为位似中心，作出△AOB的位似三角形，并把△ABO的边长缩小到原来的 $\frac{1}{2}$ .

(2)、点 $C (- 2.4 ， 3.6)$ 是边AB上一点，根据你所画图形写出它对应点的坐标.

查看试题解析
19. 在一个不透明的盒子里装着只有颜色不同的黑、白两种球共5个，小明做摸球实验，他将盒子里面的球搅匀后从中随机摸出一球记下颜色，再把它放回盒子，不断重复上述过程实验n次，下表是小明“摸到白球”的频数、频率统计表.
摸球实验次数n
10
100
150
200
500
…
摸到白球的频数m
2
22
31
39
101
…
摸到白球的频率p
0.200
0.220
0.207
0.195
0.202
…

(1)、观察上表，可以推测，摸一次摸到白球的概率为.

(2)、请你估计盒子里白球个数.

(3)、若往盒子中同时放入x个白球和y个黑球，从盒子中随机取出一个白球的概率是0.25，求y与x之间的函数关系式.

查看试题解析
20. 如图，葡萄园大棚支架的顶部形如等腰△ABC.经测量，钢条AD⊥BC，BC＝600cm，∠B＝38°.（精确到1cm，参考数据：sin 38°≈0.616，cos 38°≈0.788，tan 38°≈0.781）

(1)、求钢条AB的长.

(2)、为了加固支架，现在顶部加两根钢条DE和DF，已知DE⊥AB于点E，DF⊥AC于点F，求DE的长.

查看试题解析
21. 如图，矩形DEFG的四个顶点分别在正三角形ABC的边上，已知△ABC的边长为4，记矩形DEFG的面积为S，线段BE为x.

(1)、求S关于x的函数表达式.

(2)、当 $S = \sqrt{3}$ 时，求x的值.

查看试题解析
22. 如图，已知 $⊙ O$ 是等腰△ABC的外接圆，且AB＝AC，点D是 $\overset{⌢}{A B}$ 上一点，连结BD并延长至点E，连结AD，CD.

(1)、求证：DA平分∠EDC.

(2)、若∠EDA＝72°，求 $\overset{⌢}{B C}$ 的度数.

查看试题解析
23. 在平面直角坐标系xOy中，如果抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 上存在一对点P和 $P^{'}$ ，且它们关于坐标原点O对称，那么我们把点P和 $P^{'}$ 叫做这条抛物线的成对点.

(1)、已知点 $P (- 2 ， m)$ 与 $P^{'}$ 是抛物线 $y = x^{2} - 2 x - 4$ 的成对点，求 $P^{'}$ 的坐标.

(2)、如图，已知点A与C为抛物线 $y = - x^{2} - 2 x + c$ 的成对点，且A为该抛物线的顶点.
①求c的值.

②若这条抛物线的对称轴与x轴交于点B，连结AC，BC，点D是射线AB上一点.如果∠ADC＝∠ACB，求点D的坐标.

查看试题解析
24. 如图，在矩形ABCD中，AD＝4cm，AB＝2cm，点E从点B出发，沿BC以每秒1cm的速度向点C匀速运动，当点E到达点C时停止运动，设点E的运动时间为t秒.连结AE，过点E作EF⊥AE，E为垂足，点F在直线BC的上方，且 $\frac{E F}{A E} = \frac{1}{2}$ ，以点F为圆心，FE为半径作圆，连结CF.

(1)、当 $t = 1$ 时，判断点C与 $⊙ F$ 的位置关系.

(2)、当 $t > 1$ 时， $⊙ F$ 是否会与矩形ABCD的边所在的直线相切，若相切，求出t的值，若不相切，请说明理由.

(3)、直接写出点F的运动路径长.

查看试题解析

速度x（km/h）	0	5	10	15	20	a	…
刹车距离y（m）	0	0.75	2	3.75	6	12	…

摸球实验次数n	10	100	150	200	500	…
摸到白球的频数m	2	22	31	39	101	…
摸到白球的频率p	0.200	0.220	0.207	0.195	0.202	…