广西壮族自治区贺州市平桂区2021-2022学年九年级上学期期末数学试卷

试卷更新日期：2022-03-17 类型：期末考试

进入出卷网下载

一、单选题

1. 下列函数表达式中，一定为二次函数的是（）

A、 $y = 5 x - 1$ B、 $y = a x^{2} + b x + c$ C、 $y = 3 x^{2} + 1$ D、 $y = x^{2} + \frac{1}{x}$

查看试题解析
2. 若点 $A (a ， 2)$ 在反比例函数 $y = \frac{6}{x}$ 的图象上，则a的值是（）

A、12 B、8 C、4 D、3

查看试题解析
3. 下列说法正确的是（）

A、正五边形都相似 B、等腰三角形都相似 C、直角三角形都相似 D、钝角三角形都相似

查看试题解析
4. 若 $\frac{y}{x} = \frac{1}{2}$ ，则 $\frac{x + y}{x}$ 的值是（）

A、 $\frac{5}{2}$ B、 $\frac{3}{2}$ C、1 D、 $\frac{2}{3}$

查看试题解析
5. 把抛物线 $y = x^{2}$ 向右平移3个单位，所得抛物线的解析式为（）

A、 $y = x^{2} + 3$ B、 $y = (x - 3)^{2}$ C、 $y = x^{2} - 3$ D、 $y = (x + 3)^{2}$

查看试题解析
6. 对于反比例函数 $y = \frac{2}{x}$ ，下列说法不正确的是（）

A、当 $x > 0$ 时，y随x的增大而增大 B、当 $x < 0$ 时，y随x的增大而减小 C、点（-2，-1）在它的图象上 D、它的图象在第一、三象限

查看试题解析
7. 如图，以点O为位似中心，将△OAB放大后得到△OCD，若 $A B = 3$ ， $C D = 5$ ， $O B = 4$ ，则线段BD长为（）

A、 $\frac{20}{3}$ B、6 C、 $\frac{8}{3}$ D、 $\frac{2}{3}$

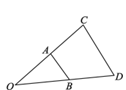查看试题解析
8.
在△ABC中，D、E为边AB、AC的中点，已知△ADE的面积为4，那么△ABC的面积是（　　）

A、8 B、12 C、16 D、20

查看试题解析
9. 在△ABC中， ${(2 c o s A - \sqrt{3})}^{2} + | 1 - t a n B | = 0$ ，则△ABC一定是（）

A、钝角三角形 B、直角三角形 C、等腰直角三角形 D、锐角三角形

查看试题解析
10. 如图，明明家（图中点O处）门前有一条东西走向的公路，经测得有一水塔（图中点A处）在距她家北偏东60°方向的500米处，那么水塔所在的位置到这条公路的距离是（）

A、 $250 \sqrt{3}$ 米 B、250米 C、 $\frac{500 \sqrt{3}}{3}$ 米 D、 $500 \sqrt{2}$ 米

查看试题解析
11. 一次函数 $y = k_{1} k_{2} x + b (k_{1} k_{2} \neq 0)$ 与反比例函数 $y = \frac{k_{2}}{x}$ 上的图象在同一直角坐标系下的大致图象如图所示，则 $k_{1}$ 、b的取值范围是（）

A、 $k_{1} > 0$ ， $b > 0$ B、 $k_{1} < 0$ ， $b > 0$ C、 $k_{1} < 0$ ， $b < 0$ D、 $k_{1} > 0$ ， $b < 0$

查看试题解析
12. 如图，正方形ABCD的边长为4cm，动点P，Q同时从点A处出发，以2cm/s小的速度分别沿 $A \to B \to C$ 和 $A \to D \to C$ 的路径向点C运动.设运动时间为x（单位：s），以P、B、D、Q为顶点的图形面积的为y（单位： $c m^{2}$ ），则下列图象中可表示y与x（ $0 \leq x \leq 4$ 且 $x \neq 2$ ）之间的函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 在Rt△ABC中， $∠ C = 90 °$ ， $a = 4$ ， $c = 5$ ，则 $c o s B =$ .

查看试题解析
14. 若将△ABC的各边都扩大为原来的2倍，则该三角形的周长会扩大为原来的倍.

查看试题解析
15. 在比例尺为1：50000的地图上，量得甲、乙两地的距离是25cm，则甲、乙两地的实际距离是km.

查看试题解析
16. 抛物线y＝x²+2x-3与x轴的交点坐标为．

查看试题解析
17. 在平行四边形ABCD中，E是AD延长线上的一点， $D E = 3 B C$ ， BE和CD相交于点F，若 $S_{△ B C F} = 5$ ，则 $S_{△ A B E} =$ .

查看试题解析
18. 已知二次函数y=ax²+2ax+3a²+3（其中x是自变量），当x≥2时，y随x的增大而增大，且﹣2≤x≤1时，y的最大值为9，则a的值为.

查看试题解析

三、解答题

19. 计算： $- 1^{2} + \sqrt{12} - {(- \frac{1}{2})}^{- 1} - 4 s i n 60 °$ .

查看试题解析
20. 当m取何值时， $y = (m + 2) x^{m^{2} + 3 m + 1}$ 是关于x的反比例函数？

查看试题解析
21. 若二次函数 $y = x^{2} + b x - 3$ 的对称轴为直线 $x = 1$ ，求关于x的方程 $x^{2} + b x - 3 = 5$ 的解.

查看试题解析
22. 二次函数y＝ax²+bx+c的图象过A（2，0），B（0，﹣1）和C（4，5）三点.

(1)、求二次函数的解析式；

(2)、设二次函数的图象与x轴的另一个交点为D，求点D的坐标.

查看试题解析
23. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $A D$ 为 $B C$ 边上的中线， $D E ⊥ A B$ 于点E.

(1)、求证： $Δ B D E ∽ Δ C A D$ ；

(2)、若 $A B = 13$ ， $B C = 10$ ，求线段 $D E$ 的长.

查看试题解析
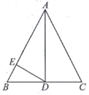24. 下课时，数学老师给大家布置了一个任务：请大家在不攀爬到楼顶上的情况下，测出学校逸夫综合楼的高度.根据老师所给的任务，小慧站在与逸夫综合楼底部B在同一水平面且距离10米的C处，通过测角器观察逸夫综合楼的顶端A，此时测角器的示数为60°，小慧又请小敏帮量得此时测角器与地面的距离CD长为1米，如图.请你帮小慧算出学校逸夫综合楼的高度（结果精确到0.1米，参考数据： $s i n 30 ° \approx 0.5$ ， $c o s 60 ° \approx 0.866$ ， $t a n 60 ° \approx 1.732$ ）.

查看试题解析
25. 如图，在矩形ABCD中， $A B = 5$ ， $B C = 12$ ，点P是矩形的对角线BD上的一个动点，且始终满足 $P E ⊥ B C$ 交BC于点E.

(1)、求证：△BEP∽△BCD

(2)、若△APD是等腰三角形，求此时线段PE的长.

查看试题解析
26. 服装店老板小李根据商场要求试销售一种成本为50元/件的T恤，商场规定试销期间T恤的单价不低于成本，且获利不高于40%.经试销发现，销售量y（件）与售价x（元/件）符合一次函数 $y = k x + b$ ，且当 $x = 60$ 时， $y = 60$ ：当 $x = 70$ 时， $y = 50$ .

(1)、求一次函数 $y = k x + b$ 的表达式：

(2)、若服装店老板小李获得的利润为W元，试写出利润W与售价x（元/件）之间的函数表达式，并求出售价定为多少元/件时，小李获得最大利润，最大利润是多少.

查看试题解析